KNN 匹配

KNN学习

KNN的基础知识

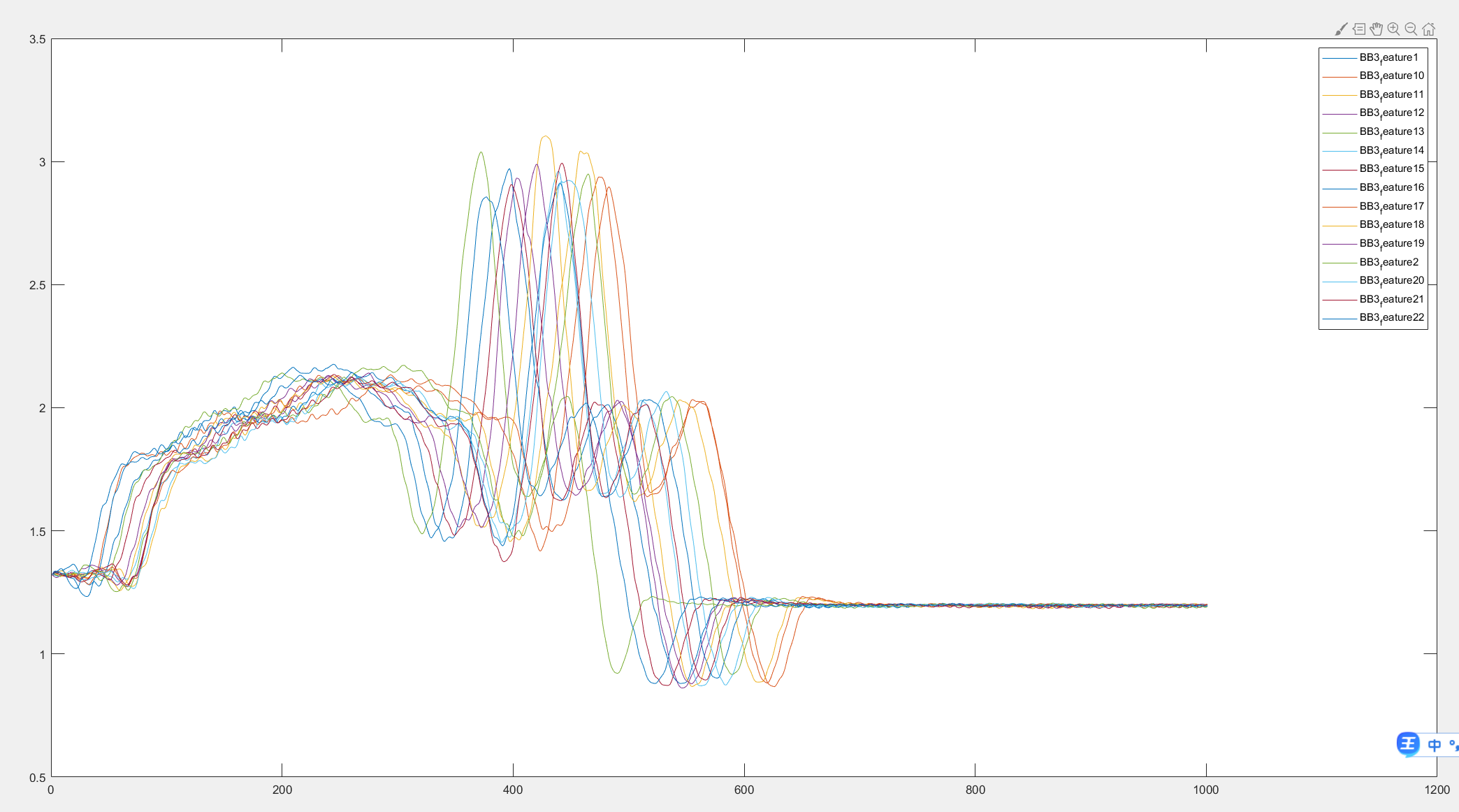
原始数据的距离图像打印

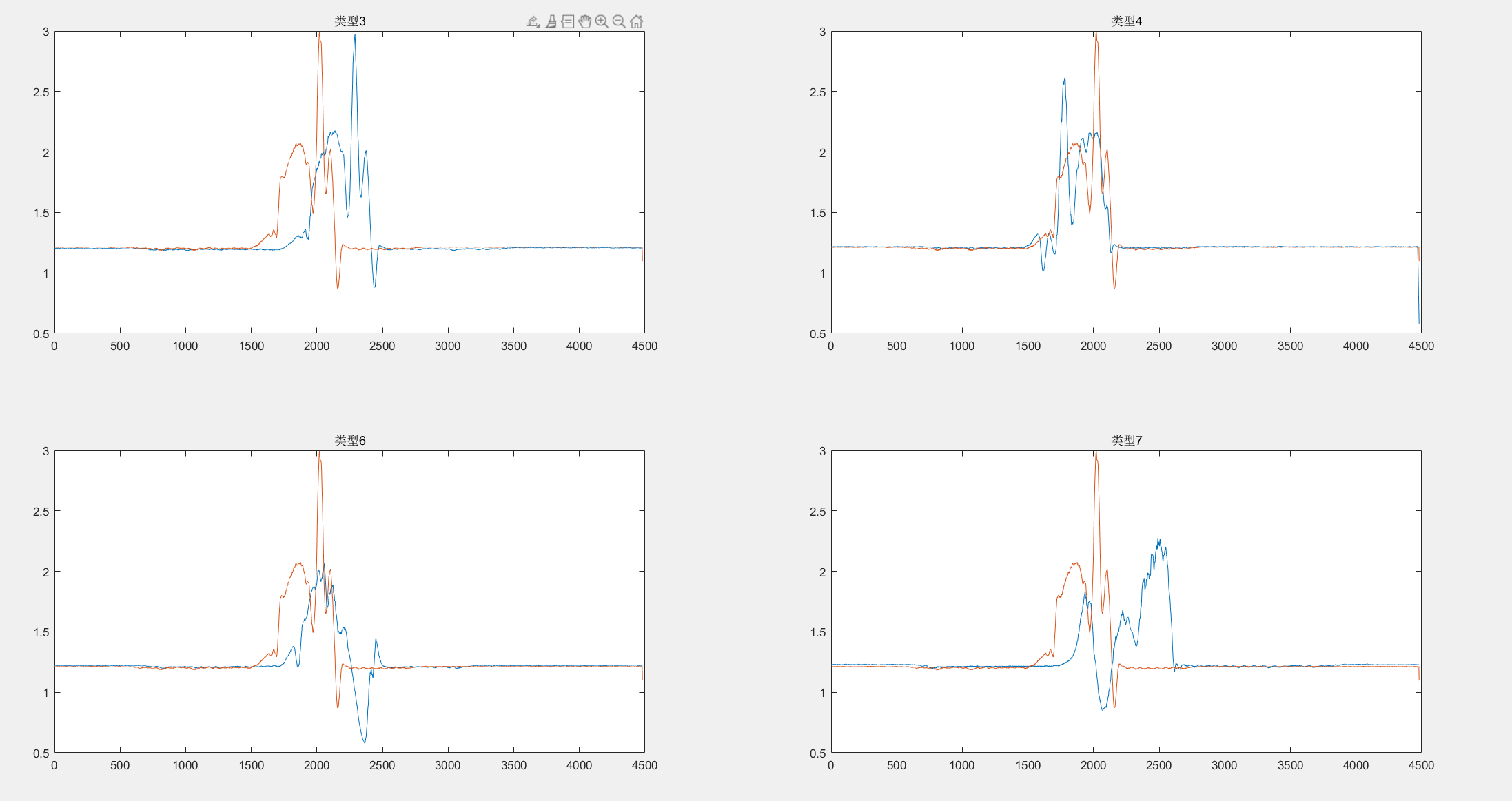
类型3的第70个数据 与类型3，4，6，7四种不同类型的第1个进行对比

欧氏距离

欧几里得度量 Euclidean Metric，Euclidean Distance：指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。

比如：在二维和三维空间中的欧氏距离就是两点之间的实际距离。

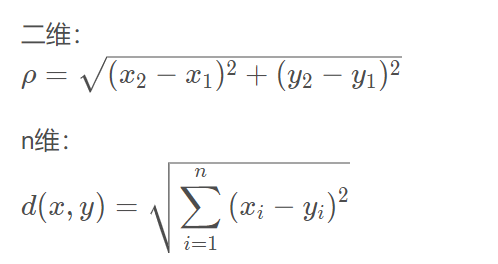
曼哈顿距离

KNN的计算方法

KNN数据的预处理

KNN数据预处理就是找到信息含有量最多的那一段信息，将前面后面的信息不加以考虑。原因是KNN计算量太大了，单片机不一定能行

因为对比不同的数据，他们的曲线形式是完全不一样的，如图所示，上次老师说不找突变点，直接全部计算(感觉好像不太行)

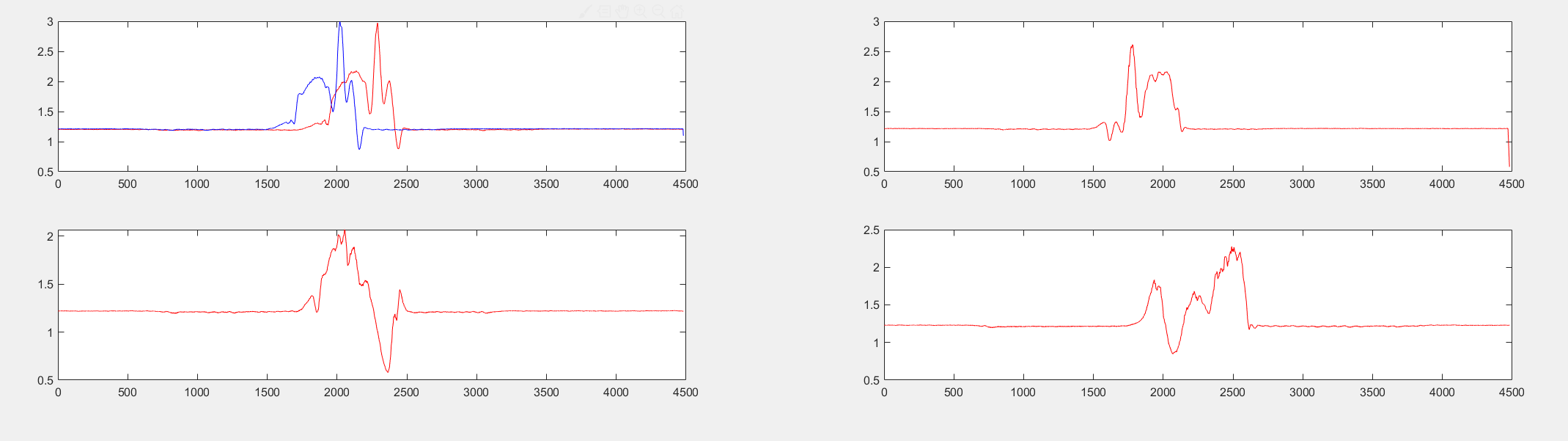
因为数据量太大，所以打算使用硬阈值进行计算，通过观察发现，电压大于1.32的时候（正常是1.2，我向上浮动了10%），然后向后推800-1000个点可以正好表达出相关的突变数据段，也就是我们需要的有用信息，如图所示

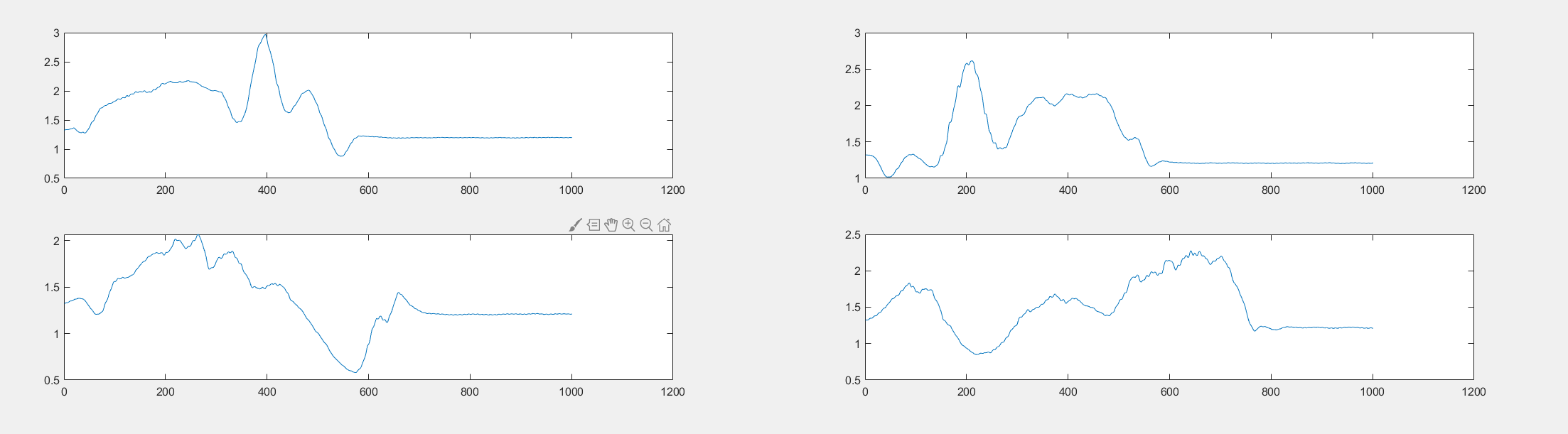
KNN测试集和训练集

我每一类都找出了其中前25组数据，我把训练集定为前15组，测试集定为后10组。（给的数据一共80组，选了25个 前期少工作量看效果）

每一组的类型都相差不大，下图是第三类的7个数据，可以看出依然有100个点不到的偏移。

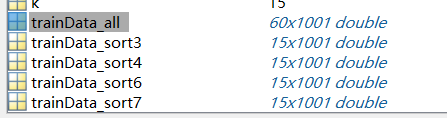
训练集的数据

训练集一类共计15个，4类共计60个一维数组，每个一维数组有1001个点

KNN的基本原理

KNN 也就是 K 近邻算法，即某个待分类元素，查看它与其他类别元素的距离，统计距离最短的 K 个邻居，K 个中属于哪个类别的多，则该分类属于哪个类别。

计算步骤：

1）算距离：给定测试对象，计算它与训练集中的每个对象的距离

2）找邻居：圈定距离最近的k个训练对象，作为测试对象的近邻

3）做分类：根据这k个近邻归属的主要类别，来对测试对象分类

K值的选取

K 值很重要，那么 K 值选择多少合适呢？

首先，K 值一般都会选择为奇数，这个很好理解，如果是偶数，就有可能出现不同分类数量一致的情况，奇数的 K 值，就能够保证一定能选出最多的那个分类。

如果 K 值选择的比较小，那么如果它的邻居中存在噪声点，就会对元素的分类产生误差，也就是会有过拟合的风险，预测结果对于近邻的元素会非常敏感。

如果 K 值选择的比较大，即距离待分类元素很远的元素也能够影响分类，那么就很难把该元素真正的分类出来，从而导致预测错误，分类模糊，有欠拟合的风险。

业界一般会使用交叉验证（Cross Validation）的思维来选取 K 值。

何为交叉验证呢，就是把训练集进一步分成训练数据（Training Data）和验证数据（Validation Data），在训练数据上取不同的 K 值进行模型训练，然后在验证数据上做验证，最终选择在验证数据里最好的 K 值作为最终的 K 值。

我们先把总样本数据分成训练集和测试集两部分，然后再把训练集分出一部分作为验证集。这样，在验证集中表现比较好的模型，就可以拿到测试集中做测试了。

KNN的代码

KNN

单个数据进行判断

首先是进行了单个数据分类是否成功，代码如下：

clear;clc;
cj3=dir('D:\比赛资料\特征提取的数据\CJ333/*.mat');
cj4=dir('D:\比赛资料\特征提取的数据\CJ444/*.mat');
cj6=dir('D:\比赛资料\特征提取的数据\CJ666/*.mat');
cj7=dir('D:\比赛资料\特征提取的数据\CJ777/*.mat');
%%
%提取训练集的数据
for k=1:15
load(['D:\比赛资料\特征提取的数据\CJ333\' cj3(k).name]);
load(['D:\比赛资料\特征提取的数据\CJ444\' cj4(k).name]);
load(['D:\比赛资料\特征提取的数据\CJ666\' cj6(k).name]);
load(['D:\比赛资料\特征提取的数据\CJ777\' cj7(k).name]);
end

%%
%构建特征训练矩阵
%类3的训练矩阵
trainData_sort3 = [BB3_feature1';BB3_feature10';BB3_feature11';BB3_feature12';BB3_feature13';BB3_feature14'; BB3_feature15'; ...
  BB3_feature16'; BB3_feature17'; BB3_feature18'; BB3_feature19'; BB3_feature2'; BB3_feature20'; BB3_feature21'; BB3_feature22'];

%类4的训练矩阵
trainData_sort4 = [BB4_feature1';BB4_feature10';BB4_feature11';BB4_feature12';BB4_feature13';BB4_feature14'; BB4_feature15'; ...
  BB4_feature16'; BB4_feature17'; BB4_feature18'; BB4_feature19'; BB4_feature2'; BB4_feature20'; BB4_feature21'; BB4_feature22'];

%类6的训练矩阵
trainData_sort6 = [BB6_feature1';BB6_feature10';BB6_feature11';BB6_feature12';BB6_feature13';BB6_feature14'; BB6_feature15'; ...
  BB6_feature16'; BB6_feature17'; BB6_feature18'; BB6_feature19'; BB6_feature2'; BB6_feature20'; BB6_feature21'; BB6_feature22'];

%类7的训练矩阵
trainData_sort7 = [BB7_feature1';BB7_feature10';BB7_feature11';BB7_feature12';BB7_feature13';BB7_feature14'; BB7_feature15'; ...
  BB7_feature16'; BB7_feature17'; BB7_feature18'; BB7_feature19'; BB7_feature2'; BB7_feature20'; BB7_feature21'; BB7_feature22'];

%总的特征训练矩阵
trainData_all = [trainData_sort3; trainData_sort4; trainData_sort6; trainData_sort7];

%设置相关的标签   标签1——类3    标签2——类4   标签3——类6  标签4——类7
trainClass_3 = repmat(1,1,15);
trainClass_4 = repmat(2,1,15);
trainClass_6 = repmat(3,1,15);
trainClass_7 = repmat(4,1,15);

trainClass_all = [trainClass_3,trainClass_4,trainClass_6,trainClass_7];  %KNN的分类标签


%%
%提取测试集数据
for k=16:25
load(['D:\比赛资料\特征提取的数据\CJ333\' cj3(k).name]);  %取出类三的16-20一共5个数据，进行初步判断
load(['D:\比赛资料\特征提取的数据\CJ444\' cj4(k).name]);
% load(['D:\比赛资料\特征提取的数据\CJ666\' cj6(k).name]);
% load(['D:\比赛资料\特征提取的数据\CJ777\' cj7(k).name]);
end


%选取一个测试集的数据
%类三的这五个数据为———— BB3_feature4, BB3_feature23, BB3_feature24, BB3_feature25, BB3_feature3
%类四的这五个数据为———— BB4_feature23, BB4_feature24, BB4_feature25, BB4_feature3, BB4_feature4
% testData  =  BB4_feature23';
% testData  =  BB4_feature23';
% testData  =  BB4_feature23';
% testData  =  BB4_feature23';
testData  =  BB3_feature4';


[N,M]=size(trainData_all);

%计算欧式距离   就是 dist =（y1-y2）^2
dist=zeros(N,1);
for i=1:N
    dist(i,:)=norm(trainData_all(i,:)-testData);
end

%将距离从小到大进行排序
[Y,I]=sort(dist,1);

%将训练数据对应的类别与训练数据排序结果对应
trainClass=trainClass_all(I);
%确定前K个点所在类别的出现频率
classNum=length(unique(trainClass));

%特征分类
K=7;
labels=zeros(1,classNum);
for i=1:K
    j=trainClass(i);
    labels(j)=labels(j)+1;
end

[~,idx]=max(labels);

%输出KNN结果
if idx == 1
fprintf('该测试数据属于类3');
    elseif idx == 2
fprintf('该测试数据属于类4');
    elseif idx == 3
fprintf('该测试数据属于类6');
    elseif idx == 4
fprintf('该测试数据属于类7');
end

实验结果

结果如下：

利用预处理后的数据，按照15个训练集，10个测试集进行。计算欧式距离为dist =（y1-y2）^2 K值选择为7，单独一个可以正确分类

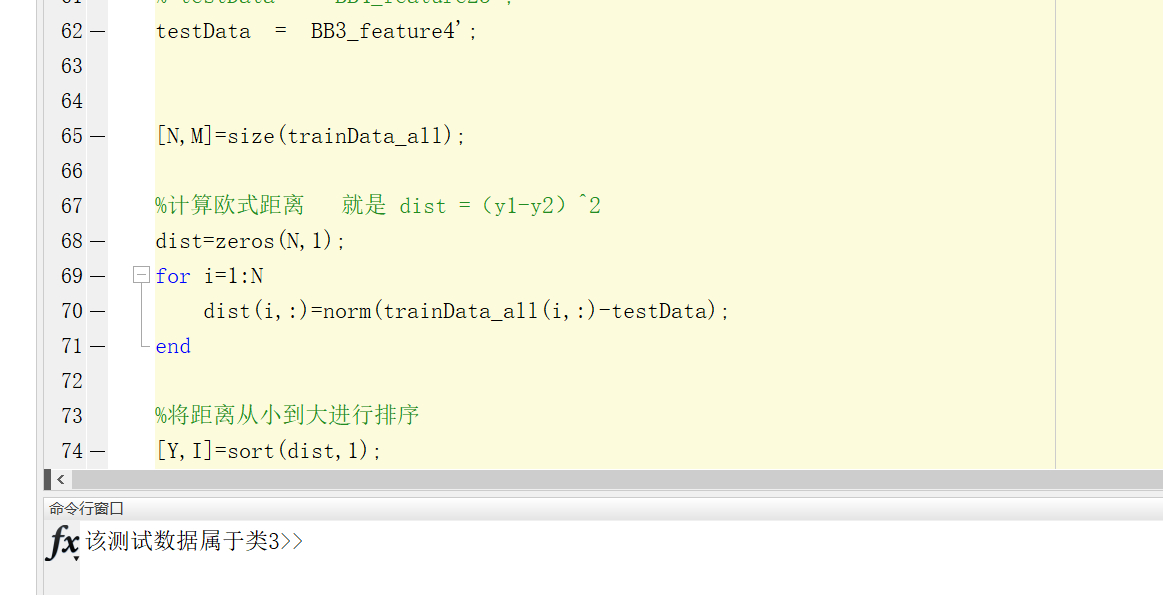
然后整体分类的正确率和错误率代码（还没写出来，不会），四个类型，一个类型测试10个，共40组数据，测试之后看正确率。

类型	类3（10个）	类4（10个错了三个）	类6（10个）	类7（10个）
正确率	100%	70%	100%	100%

总正确率 37/40=92.5%