算法的时间复杂度

时间复杂度

时间复杂度判断一个算法所编程序运行时间的多少，并不是将程序编写出来，通过在计算机上运行所消耗的时间来度量。原因很简单，一方面，解决一个问题的算法可能有很多种，一一实现的工作量无疑是巨大的，得不偿失；另一方面，不同计算机的软、硬件环境不同，即便使用同一台计算机，不同时间段其系统环境也不相同，程序的运行时间很可能会受影响，严重时甚至会导致误判。

实际场景中，我们更喜欢用一个估值来表示算法所编程序的运行时间。所谓估值，即估计的、并不准确的值。注意，虽然估值无法准确的表示算法所编程序的运行时间，但它的得来并非凭空揣测，需要经过缜密的计算后才能得出。

也就是说，表示一个算法所编程序运行时间的多少，用的并不是准确值（事实上也无法得出），而是根据合理方法得到的预估值。

那么，如何预估一个算法所编程序的运行时间呢？很简单，先分别计算程序中每条语句的执行次数，然后用总的执行次数间接表示程序的运行时间。

以一段简单的 C 语言程序为例，预估出此段程序的运行时间：

for(int i = 0 ; i < n ; i++) //<- 从 0 到 n，执行 n+1 次
{
a++; //<- 从 0 到 n-1，执行 n 次
}

可以看到，这段程序中仅有 2 行代码，其中：

• for 循环从 i 的值为 0 一直逐增至 n（注意，循环退出的时候 i 值为 n），因此 for 循环语句执行了 n+1 次；
• 而循环内部仅有一条语句，a++ 从 i 的值为 0 就开始执行，i 的值每增 1 该语句就执行一次，一直到 i 的值为 n-1，因此，a++ 语句一共执行了 n 次。

因此，整段代码中所有语句共执行了 (n+1)+n 次，即 2n+1 次。数据结构中，每条语句的执行次数，又被称为该语句的频度。整段代码的总执行次数，即整段代码的频度。

再举一个例子：

for(int i = 0 ; i < n ; i++) // n+1
{
for(int j = 0 ; j < m ; j++) // n*(m+1)
{
num++; // n*m
}
}

读者可结合注释，计算此段程序的频度为：(n+1)+n*(m+1)+n*m，简化后得 2*n*m+2*n+1。值得一提的是，不同程序的运行时间，更多场景中比较的是在最坏条件下程序的运行时间。以上面这段程序为例，最坏条件即指的是当 n、m 都为无限大时此段程序的运行时间。

要知道，当 n、m 都无限大时，我们完全就可以认为 n==m。在此基础上，2*n*m+2*n+1 又可以简化为 2*n²+2*n+1，这就是此段程序在最坏情况下的运行时间，也就是此段程序的频度。

如果比较以上 2 段程序的运行时间，即比较 2n+1 和 2*n²+2*n+1 的大小，显然当 n 无限大时，前者要远远小于后者（如图 2 所示）。 

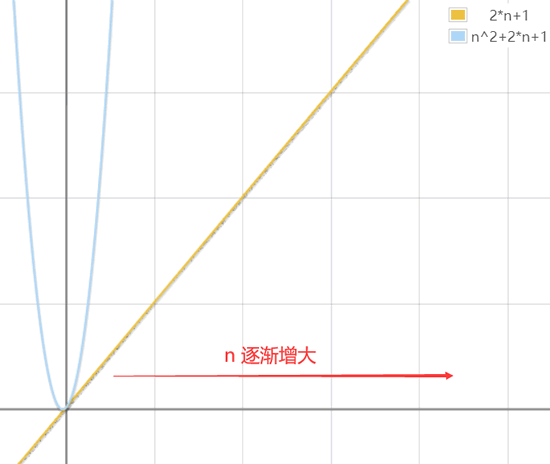
图 2 不同程序运行时间的比较

显然，第 1 段程序的运行时间更短，运行更快。

思考一个问题，类似 2n+1、2*n²+2*n+1 这样的频度，还可以再简化吗？答案是肯定的。

以 2n+1 为例，当 n 无限大时，是否在 2n 的基础上再做 +1 操作，并无关紧要，因为 2n 和 2n+1 当 n 无限大时，它们的值是无限接近的。甚至于我们还可以认为，当 n 无限大时，是否给 n 乘 2，也是无关紧要的，因为 n 是无限大，2*n 也是无限大。

再以无限大的思想来简化 2*n²+2*n+1。当 n 无限大的：

• 首先，常数 1 是可以忽略不计的；
• 其次，对于指数级的 2*n² 来说，是否在其基础上加 2*n，并无关紧要；
• 甚至于，对于是否给 n² 乘 2，也可以忽略。

因此，最终频度 2*n²+2*n+1 可以简化为 n² 。

也许很多读者对于“使用无限大的思想”简化频度表达式，并不是很清楚。没关系，这里给大家总结一下，在数据结构中，频度表达式可以这样简化：

• 去掉频度表达式中，所有的加法常数式子。例如 2n²+2n+1 简化为 2n²+2n ；
• 如果表达式有多项含有无限大变量的式子，只保留一个拥有指数最高的变量的式子。例如 2n²+2n 简化为 2n²；
• 如果最高项存在系数，且不为 1，直接去掉系数。例如 2n² 系数为 2，直接简化为 n² ；

事实上，对于一个算法（或者一段程序）来说，其最简频度往往就是最深层次的循环结构中某一条语句的执行次数。例如 2n+1 最简为 n，实际上就是 a++ 语句的执行次数；同样 2n²+2n+1 简化为  n²，实际上就是最内层循环中 num++ 语句的执行次数。

得到最简频度的基础上，为了避免人们随意使用 a、b、c 等字符来表示运行时间，需要建立统一的规范。数据结构推出了大 O 记法（注意，是大写的字母 O，不是数字 0）来表示算法（程序）的运行时间。发展至今，此方法已为大多数人所采纳。

大 O 记法的表示方法也很简单，格式如下：

O(频度)

其中，这里的频度为最简之后所得的频度。

例如，用大 O 记法表示上面 2 段程序的运行时间，则上面第一段程序的时间复杂度为 O(n)，第二段程序的时间复杂度为 O(n²)。

如下列举了常用的几种时间复杂度，以及它们之间的大小关系：

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n²)平方阶 < O(n³)(立方阶) < O(2ⁿ) (指数阶)

注意，这里仅介绍了以最坏情况下的频度作为时间复杂度，而在某些实际场景中，还可以用最好情况下的频度和最坏情况下的频度的平均值来作为算法的时间复杂度。

常见的时间复杂度量级有：

• 常数阶O(1)
• 对数阶O(logN)
• 线性阶O(n)
• 线性对数阶O(nlogN)
• 平方阶O(n²)
• 立方阶O(n³)
• K次方阶O(n^k)
• 指数阶(2^n)

上面从上至下依次的时间复杂度越来越大，执行的效率越来越低。

下面选取一些较为常用的来讲解一下（没有严格按照顺序）：

1. 常数阶O(1)

无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)，如：

int i = 1; 
int j = 2; 
++i; j++; 
int m = i + j;

上述代码在执行的时候，它消耗的时候并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用O(1)来表示它的时间复杂度。

1. 线性阶O(n)

这个在最开始的代码示例中就讲解过了，如：

for(i=1; i<=n; ++i)
{ j = i; 
 j++;
}

这段代码，for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度。

1. 对数阶O(logN)

还是先来看代码：

int i = 1; 
while(i<n) 
{ 
    i = i * 2; 
}

从上面代码可以看到，在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。我们试着求解一下，假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2^n
也就是说当循环 log2^n 次以后，这个代码就结束了。因此这个代码的时间复杂度为：O(logn)

1. 线性对数阶O(nlogN)

线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)。

就拿上面的代码加一点修改来举例：

for(m=1; m<n; m++) { 
    i = 1;
    while(i<n)  {
        i = i * 2; 
    } 
}

1. 平方阶O(n²)

平方阶O(n²) 就更容易理解了，如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²) 了。
举例：

for(x=1; i<=n; x++) { for(i=1; i<=n; i++) { j = i; j++; } }

这段代码其实就是嵌套了2层n循环，它的时间复杂度就是 O(n*n)，即 O(n²)
如果将其中一层循环的n改成m，即：

for(x=1; i<=m; x++) { for(i=1; i<=n; i++) { j = i; j++; } }

那它的时间复杂度就变成了 O(m*n)

1. 立方阶O(n³)、K次方阶O(n^k)

参考上面的O(n²) 去理解就好了，O(n³)相当于三层n循环，其它的类似。