LeetCode刷题--DFS与BFS --岛屿的最大面积与地图分析

　　　　题目均来自于力扣，最近力扣正在举行每日一题的活动，有兴趣的小伙伴可以多参与哦。

　　　　先来看看岛屿的最大面积的题目描述吧。

 

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

 

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/max-area-of-island

　　翻译一下题目，就是在二维矩阵中寻找相邻皆为1的最大面积。注意这里的相邻指的是row索引差值为1或是column索引差值为1。

　　笔者从最朴素的想法开始，双重循环遍历整个矩阵，向右向下寻找，如果遇到相邻的陆地就加入，从而在O(n)的时间内计算出结果。但是仔细思考一下就能发现这种想法的漏洞。

1. 对于行n遇到的陆地（1），需要记录行n-1才能决定是否要加入到整个陆地面积中去
2. 对于形如[[1,0,1],[1,1,1]...]的数据在遍历第一行时认为有“两座小岛”，在第二行时需要将其合并)
3. 不易于判断每座独立岛屿的面积大小

　　再来看看DFS的做法是怎样的，Show code：

public class Solution {
        public int MaxAreaOfIsland(int[][] grid)
        {
            int size = 0;

            for (int i = 0; i < grid.Length; i++)
            {
                for (int j = 0; j < grid[0].Length; j++)
                {
                    var temp = dfs(grid, i, j);

                    size = temp > size ? temp : size;
                }
            }

            return size;
        }

        private int dfs(int[][] grid, int row, int column)
        {
            if (row < 0 || column < 0 || row >= grid.Length || column >= grid[0].Length || grid[row][column] == 0)
            {
                return 0;
            }

            grid[row][column] = 0;

            int[] rowFlag = new int[4] { 1, -1, 0, 0 };
            int[] columnFlag = new int[4] { 0, 0, 1, -1 };

            int size = 1;

            for (int i = 0; i < 4; i++)
            {
                size += dfs(grid, row + rowFlag[i], column + columnFlag[i]);
            }

            return size;
        }

}

　　这种解法也比较直观，在MaxAreaOfIsand中，依次判断了每个结点所在的岛屿的面积大小并取最大值，最后取到的最大值自然就是岛屿的最大面积。

　　而在DFS算法中也比较清晰，首先是递归终止条件，超出边界或者是‘海洋’就停止这次的递归。有趣的地方是对于满足条件的‘岛屿’，直接先将其修改为‘海洋’.（grid[row][column]= 0）。这里是为了防止重复的遍历。再来就是对于矩阵类型的题目来说，一组很有意思的数组, rowFlag与columnFlag,将遍历四个方向翻译成遍历数组。 然后开始依次判断该位置四个方向的位置是否满足加入岛屿的条件，并最终返回。

　　当然上面这种解法不是最优的，优化解法可以看看官方的利用栈进行优化，当然，这道题目也是可以用BFS来解决的。

 

BFS

1162 地图分析

你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

 

示例 1：

 

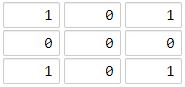
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。
示例 2：

 

输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/as-far-from-land-as-possible
　　

　　受到前面一道题的启发，这个题目笔者上来就考虑使用DFS进行计算。笔者code如下：

        public int MaxDistance(int[][] grid)
        {
            var result = -1;

            for (int i = 0; i < grid.Length; i++)
            {
                for (int j = 0; j < grid.Length; j++)
                {
                    if (grid[i][j] == 1)
                    {
                        var temp = distanceDfs(grid, 0, 0);

                        result = result < temp ? temp : result;
                    }
                }
            }

            return result;
        }

        private int distanceDfs(int[][] grid, int row, int column)
        {
            if (row < 0 || column < 0 || row >= grid.Length || column >= grid.Length)
            {
                return 0;
            }

            int[] rowf = new int[] { 1, 0 };
            int[] colf = new int[] { 0, 1 };

            int disctance = int.MinValue;

            var guid = Guid.NewGuid().ToString();

            for (int i = 0; i < 2; i++)
            {
                int temp = 0;

                Console.WriteLine($"id:{guid.ToString()} Current index row:{row}, column:{column}");

                if (row + rowf[i] < grid.Length && column + colf[i] < grid.Length && grid[row + rowf[i]][column + colf[i]] == 0)
                {
                    Console.WriteLine($"id:{guid.ToString()} Next Current index row:{row + rowf[i]}, column:{column + colf[i]}");
                    temp = 1 + distanceDfs(grid, row + rowf[i], column + colf[i]);
                }


                disctance = disctance < temp ? temp : disctance;
            }

            Console.WriteLine($"id:{guid.ToString()} Distance:{disctance}");
            return disctance;
        }

　　当然最终这个方法计算出的结果是不正确的，并且为了调试方便，加入了guid进行每次递归内的数据查看。分析一下没有正确算出答案的原因：这道题其实与岛屿的最大面积看起来类似,但最大面积有着这样一个条件，同一岛屿内点与点之间是相连的。笔者套用这样的方法，边界值又没有处理清楚，就很容易发生混乱，不好理解。

　　直接来看看官方的解法吧（C++版本）：

class Solution {
public:
    static constexpr int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    static constexpr int MAX_N = 100 + 5;

    struct Coordinate {
        int x, y, step;
    };

    int n, m;
    vector<vector<int>> a;

    bool vis[MAX_N][MAX_N];

    int findNearestLand(int x, int y) {
        memset(vis, 0, sizeof vis);
        queue <Coordinate> q;
        q.push({x, y, 0});
        vis[x][y] = 1;
        while (!q.empty()) {
            auto f = q.front(); q.pop();
            for (int i = 0; i < 4; ++i) {
                int nx = f.x + dx[i], ny = f.y + dy[i];
                if (!(nx >= 0 && nx <= n - 1 && ny >= 0 && ny <= m - 1)) continue;
                if (!vis[nx][ny]) {
                    q.push({nx, ny, f.step + 1});
                    vis[nx][ny] = 1;
                    if (a[nx][ny]) return f.step + 1;
                }
            }
        }
        return -1;
    }
    
    int maxDistance(vector<vector<int>>& grid) {
        this->n = grid.size();
        this->m = grid.at(0).size();
        a = grid;
        int ans = -1;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (!a[i][j]) {
                    ans = max(ans, findNearestLand(i, j));
                }
            }
        }
        return ans;
    }
};

　　重点在于搜索状态的确定，这里使用‘曼哈顿距离’来作为搜索状态，而递归终止条件则是遇到了“陆地”。因此流程是依次BFS每个非陆地的结点计算。当然这个题目也不止一种解法，另一种的传送门在这里。