聚类算法(一)

• 查看
  

• 案例1

import sklearn.cluster as sc
import numpy as np
import matplotlib.pyplot as mp
 
# 一维数据 划分成3类 找点  三维 四维 一样的画法。
# 分类（class）与聚类（cluster）不同（物以类聚），分类是有监督学习模型，聚类属于无监督学习模型。聚类讲究使用一些算法把样本划分为n个群落。一般情况下，这种算法都需要计算欧氏距离
# K均值算法 KMeans 聚类算法
# 第一步：随机选择k个样本作为k个聚类的中心，计算每个样本到各个聚类中心的欧氏距离，将该样本分配到与之距离最近的聚类中心所在的类别中。
# 第二步：根据第一步所得到的聚类划分，分别计算每个聚类的几何中心，将几何中心作为新的聚类中心，重复第一步，直到计算所得几何中心与聚类中心重合或接近重合为止。
 
# 读取样本# 读取样本 一列x 一列y  没有输出 人为分成4堆
x = np.loadtxt('.\multiple3.txt', delimiter=',')
 
# 划分3个聚类
model = sc.KMeans(n_clusters=3)
# 拟合  训练
model.fit(x)
# 结果一样 预测某个点 是属于哪一类的。。。  如果有了新的样本点 。你再去调用predict 方法去预测 属于 哪一类 。。。。
# pred_y = model.predict(x)
#  0 1 2 3
pred_y = model.labels_
# 打印出所有的label
print(pred_y, "聚成多少类")
print(model.cluster_centers_, " 聚类中心")
 
# 输出每个点所属的聚类中心
for i in range(len(x)):
    print("Point:", x[i], " belongs to cluster:", pred_y[i], " with center:", model.cluster_centers_ [pred_y[i]])
# 在这个例子中，我们使用了scikit-learn库中的KMeans类，将数据集X分成3个聚类。我们通过调用fit()方法来训练KMeans模型，
# 然后使用cluster_centers_属性获取聚类中心。最后，我们使用labels_属性获取每个点所属的聚类中心标签，并使用这些标签来确定每个点所属的聚类中心。
 
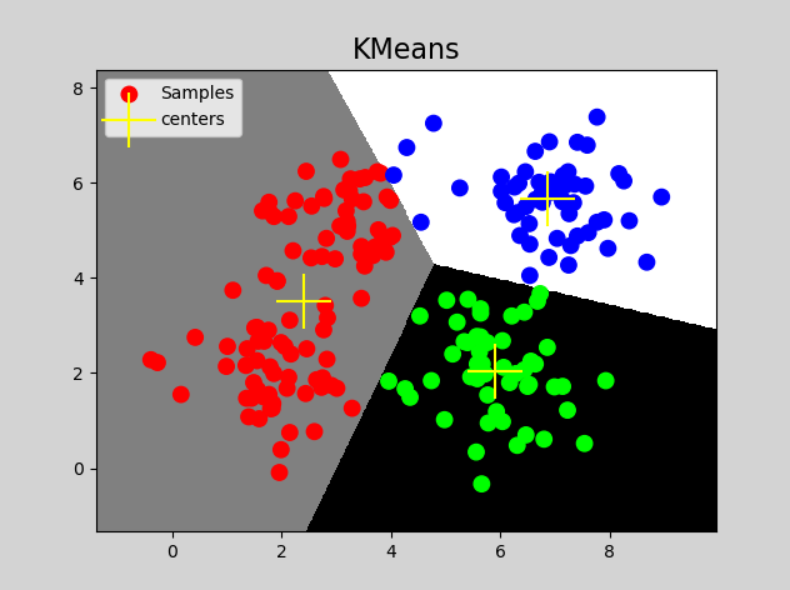
# 绘制图像
mp.figure('KMeans', facecolor='lightgray')
mp.title('KMeans', fontsize=16)
# 绘制分类边界线
n = 500
l, r = x[:,0].min()-1, x[:,0].max()+1
b, t = x[:,1].min()-1, x[:,1].max()+1
grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), 
	        				 np.linspace(b, t, n))
# 根据业务，模拟预测
mesh_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
grid_z = model.predict(mesh_x)
# 把grid_z 变维：(500,500)
grid_z = grid_z.reshape(grid_x.shape)
mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray')
 
mp.scatter(x[:,0], x[:,1], c=pred_y, cmap='brg_r',	label='Samples', s=80)
centers = model.cluster_centers_
# 获取训练结果的聚类中心 图四个中心点
# 获取训练结果的聚类中心
print(centers)
mp.scatter(centers[:,0], centers[:,1], s=1000,	marker='+', color='yellow', label='centers')
# mp.scatter(centers[:,0], centers[:,1], s=1000,marker='+', color='yellow', label='centers')
 
mp.legend()
mp.show()

查看详情

• 控制台打印

[1 1 0 2 1 2 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1
 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1
 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 0 1 0 2 1 1 0 2 1 1 0 2 1 1 0
 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 2 0 2 1 1 0 2 1 1 0 2 1 1 0 2
 1 1 0 2 1 2 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2 1
 1 0 2 1 1 0 2 1 1 0 2 1 1 0 2] 聚成多少类
[[5.91196078 2.04980392]
 [2.40645833 3.51822917]
 [6.87283019 5.66490566]]  聚类中心
Point: [ 1.96 -0.09]  belongs to cluster: 1  with center: [2.40645833 3.51822917]
Point: [2.84 3.16]  belongs to cluster: 1  with center: [2.40645833 3.51822917]
Point: [4.74 1.84]  belongs to cluster: 0  with center: [5.91196078 2.04980392]
//。。。
Point: [7.26 5.35]  belongs to cluster: 2  with center: [6.87283019 5.66490566]
[[5.91196078 2.04980392]
 [2.40645833 3.51822917]
 [6.87283019 5.66490566]]

• 输出