【图嵌入】DeepWalk 和 Node2Vec

DeepWalk

与词嵌入类似，图嵌入基本理念是基于相邻顶点的关系，将目的顶点映射为稠密向量，以数值化的方式表达图中的信息，以便在下游任务中运用。

Word2Vec根据词与词的共现关系学习向量的表示，DeepWalk受其启发。它通过随机游走的方式提取顶点序列，再用Word2Vec模型根据顶点和顶点的共现关系，学习顶点的向量表示。可以理解为用文字把图的内容表达出来，如下图所示。

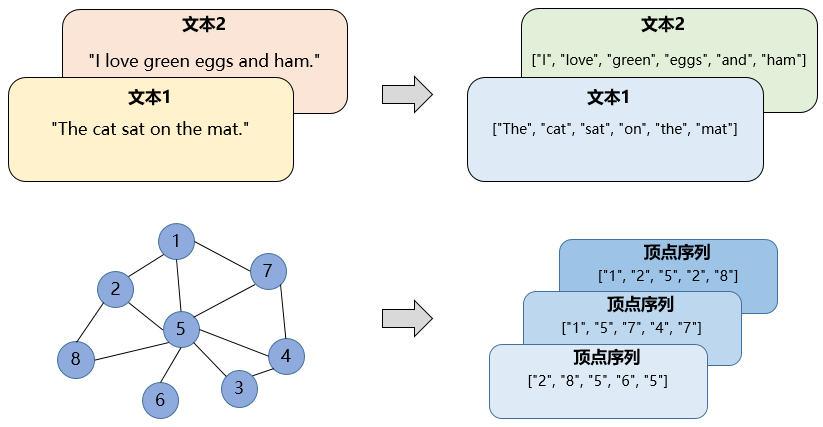
DeepWalk训练图表示的整个过程大致可以分为2步：

1. 随机游走提取顶点序列
2. 使用skip-gram学习顶点嵌入

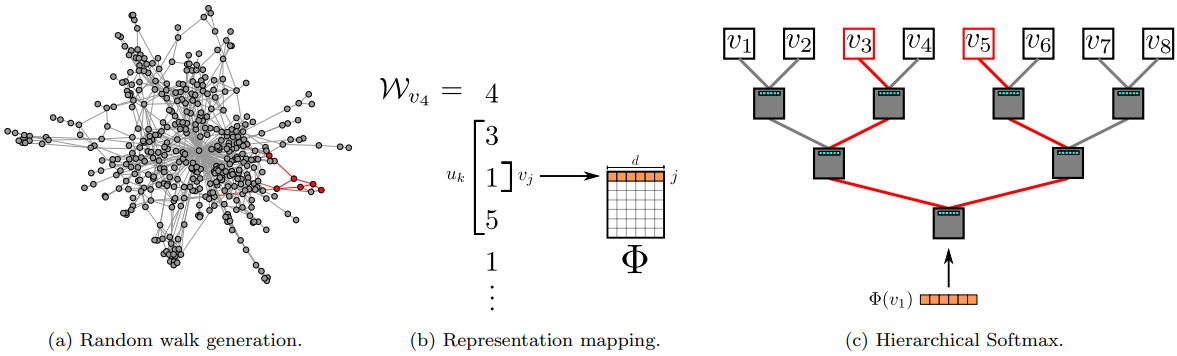
训练时采用层次Softmax（Hierarchical Softmax）优化算法，避免计算所有词的softmax。

https://www.hankcs.com/nlp/word2vec.html

https://www.cnblogs.com/pinard/p/7243513.html

Node2Vec

DeepWalk不适用于有权图，它无法学习边上的权重信息。Node2Vec可以看作DeepWalk的扩展，它学习嵌入的过程也可以分两步：

1. 二阶随机游走（\(2^{nd} \quad order \quad random \quad walk\)）
2. 使用skip-gram学习顶点嵌入

可以看到与DeepWalk的区别就在于游走的方式，在二阶随机游走中，转移概率 \(\pi_{vx}\) 受权值 \(w_{vx}\) 影响（无权图中\(w_{vx}\)为1）：

\[\pi_{vx}=\alpha_{pq}(t,x) \cdot w_{vx} \]

其中，

\[\alpha_{pq}(t,x)=\left\{ \begin{aligned} \frac{1}{p}, \quad & if\quad{d_{tx}=0} \\ 1, \quad & if\quad{d_{tx}=1} \\ \frac{1}{q}, \quad & if\quad{d_{tx}=2} \end{aligned} \right. \]

\(\alpha_{pq}\) 的取值由 \(p\) 和 \(q\) 决定，\(d_{tx}\) 是顶点 \(t\) 和 \(x\) 的最短路径。

\(d_{tx}=0\)说明\(x\)就是\(t\)，\(d_{tx}=1\)说明\(x\)和\(t\)邻接，\(d_{tx}=2\)说明\(x\)和\(t\)不是邻接的。

算法通过\(p\)、\(q\)两个超参数来控制游走到不同顶点的概率。以下图为例，图中阐述了从上一顶点 \(t\) 游走到当前顶点 \(v\)，准备估计如何游走到下一个顶点的过程。

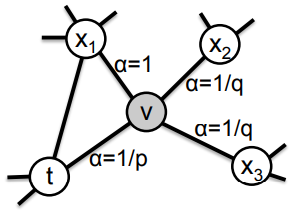
• \(q\)：控制“向内”还是“向外”游走。若\(q > 1\)，倾向于访问与 \(t\) 接近的顶点，若 \(q<1\) 则倾向于访问远离 \(t\) 的顶点。
• \(p\)：控制重复访问刚刚访问过的顶点的概率。若设置的值较大，就不大会刚问刚刚访问过的顶点。若设置的值较小，那就可能回路返回一步。

还有一个值得注意的地方，与DeepWalk不同，Node2Vec在提取顶点序列时，不再是简单地随机取邻居顶点，而是采用了Alias算法。

Alias采样是为了加快采样速度，初始化后的采样时间复杂度为\(O(1)\)，但需要存储 accept 和 alias 两个数组，空间复杂度为\(O(2N)\)。这里简单介绍一下。

给定如下离散概率分布，有 \(N\)个 （这里是4）可能发生的事件。每列矩形面积表示该事件发生的概率，柱状图中所有矩形的面积之和为 1。

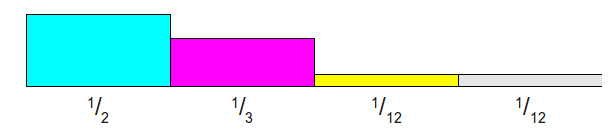
将每个事件的发生的概率乘以 \(N\)，此时会有部分矩形的面积大于1，部分矩形的面积小于1。切割面积大于1的矩形，填补到面积小于1的矩形上，并且每一列至多由两个事件的矩形构成，最终组成一个面积为 \(1\times N\) 的矩形。

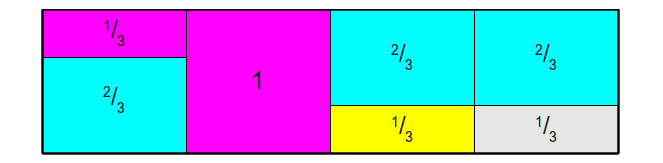
再根据这个矩形，转换成相应的Accept表和Alias表。

Node2Vec在随机游走之前会进行初始化，获取 alias_nodes 和 alias_edges 。alias_nodes 存储每个顶点决定下一个访问的点所需要的alias表，alias_edges则存储由\((t, v)\)边访问到顶点\(v\)的时候决定下一个访问点所需要的alias表。

alias_nodes与alias_edges的差别在于，alias_nodes不考虑当前顶点之前访问的顶点，它用在游走最开始的时候，此时没有“上一个顶点”。

关于 alias 采样算法更详细的内容，可以参考下面两个链接。

https://shomy.top/2017/05/09/alias-method-sampling/

https://blog.csdn.net/manmanxiaowugun/article/details/90170193

后面就跟DeepWalk一样了，但是原作者在训练Word2Vec模型的时候，没有采用层次Softmax。

代码

https://gitee.com/dogecheng/python/blob/master/graph/DeepWalk_and_Node2Vec.ipynb

DeepWalk 可视化

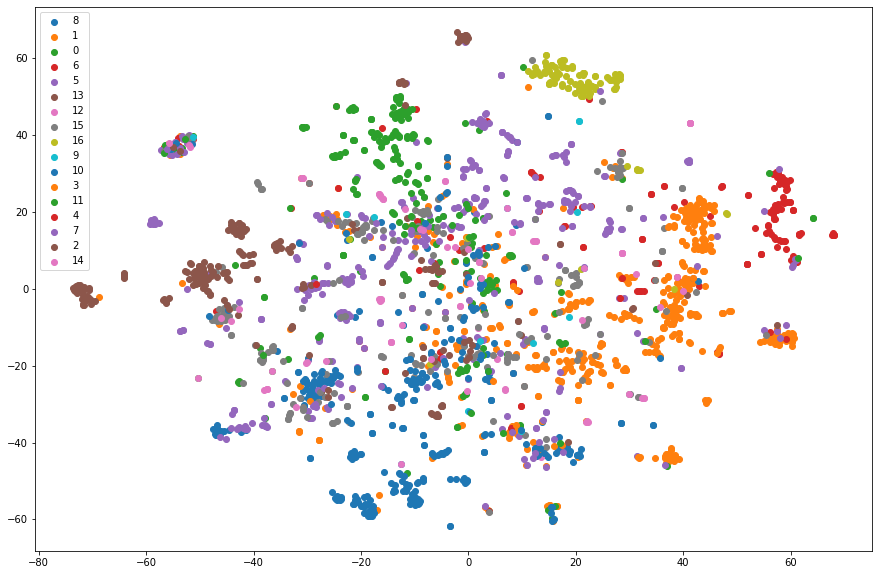
Node2Vec 可视化

参考资料

腾讯安全威胁情报中心“明厨亮灶”工程：基于域名图谱嵌入的恶意域名挖掘

DeepWalk: Online Learning of Social Representations

node2vec: Scalable Feature Learning for Networks

【Graph Embedding】DeepWalk：算法原理，实现和应用

【Graph Embedding】node2vec：算法原理，实现和应用

node2vec随机游走实现思路

Alias Method离散分布随机取样

理解node2vec

node2vec