【读书】集异璧之大成

1

　　《哥德尔、埃舍尔、巴赫：集异璧之大成》(Gödel, Escher, Bach: an Eternal Golden Braid, 下文简称GEB)的作者是美国学者侯世达(Douglas Richard Hofstadter)，其研究专业集中在认知科学与计算机科学。离散数学是计算机科学(Computer Science, CS)专业的必修课，在北大被分为三门课程讲授，即集合论与图论、代数结构与组合数学、数理逻辑。2017年春，正在修读CS双学位(软双)的我选修了数理逻辑课，机缘巧合之下了解到这本书。如果你对逻辑学(尤其是数理逻辑)感兴趣，而又不愿意学习相关教科书，或许GEB可以满足你的需求。

Figure 1. GEB目录(节选)

　　在篇章结构上，每一个(带有章节号的)章节在着重讨论逻辑学后，都有一个对话体的短文讨论巴赫的音乐，如导言后面的“三部创意曲”，第二章后面的“无伴奏阿基里斯奏鸣曲”等。遗憾的是，因缺乏基本的乐理知识，我几乎完全看不懂关于巴赫的小节，幸而此书之重点主要还是在逻辑学，对音乐及艺术的讲述更多的还是用于类比，或说是在其中寻找逻辑的影子。

　　本篇读书笔记的对应范围为原书的导言部分，并将重点讨论哥德尔不完备定理。

2

　　导言简要介绍了巴赫与其音乐、艾舍尔与其艺术、哥德尔与逻辑学。

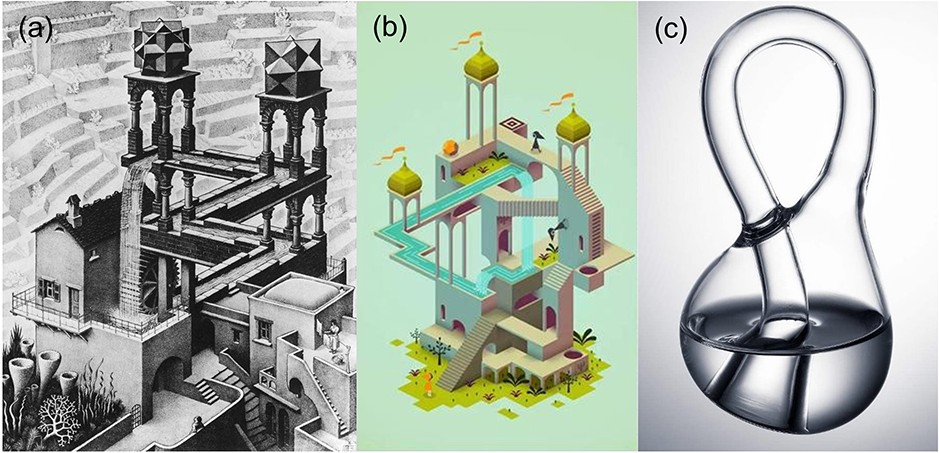
Figure 2. (a) 画作《瀑布》(Waterfall), 艾舍尔(M. C. Escher), 1961; (b) 游戏《纪念碑谷》; (c) 克莱因瓶.

　　艾舍尔的《瀑布》非常出名，尤其是游戏纪念碑谷火爆全球之后更为大家所熟知，此画利用视错觉在纸面上创造出三维空间中不可能的图景（类似地，无法区分里外的克莱因瓶也无法在三维空间中构建）。这种图画本身就存在着悖论的影子。

　　讲到哥德尔的时候首先提到的是“说谎者悖论”：埃庇米尼得斯(Epimenides)是古希腊时期的克里特岛人，他说：“所有克里特人都是骗子”。这句话更广为人知的形式即“我说的这句话是谎话。”这句话中包含了一个自指(自我指代, self-reference)，形成了一个悖论。

　　接着作者提到的是罗素悖论，它看起来与理发师悖论非常相似，它是这样表述的：

　　“设有一性质P，并立以一性质函数P(x)，且其中的自变量x有此特性：“x∉{P(x)}”，现假设由性质P能够确定一个满足性质P的集合A——也就是说“A={x|x∉A}”。那么现在的问题是：A∈A是否成立？

　　首先，若A∈A，则A是A的元素，那么A不具有性质P，由命题函数P可以得知A∉A；

　　其次，若A∉A，根据定义，A是由所有满足性质P的类组成，也就是说，A具有性质P，所以A∈A。”

　　“Define Naive Set Theory (NST) as the theory of predicate logic with a binary predicate ∈ and the following axiom schema of unrestricted comprehension: ∃y∀x(x∈y ⇔ φ(x)), for any formula φ with only the variable x free. Substitute x∉x for φ(x). Then by existential instantiation (reusing the symbol y) and universal instantiation we have y∈y ⇔ y∉y a contradiction. Therefore, NST is inconsistent.”

　　有知乎回答认为理发师悖论与罗素悖论完全不同，理发师悖论存在严重误导，理发师悖论完全符合归谬论证的形式，它只是证明了“给且仅给不给自己刮胡子的人刮胡子”的理发师是不存在的，这么简单的谬论根本不可能引起第三次数学危机。我对此持保留意见，一来罗素悖论的解决跟这名答主提到的理发师悖论的解决非常相似，就是直接把这类涉及自指的集合排除出讨论范围，二来以自然语言形式表达的谬论本来就是拿来帮助理解的(显然理发师悖论比罗素悖论更好理解，而将理发师的理发对象形式化后二者本质并无不同)，甚至根据维基百科理发师悖论本来就是罗素自己提出来通俗化罗素悖论的。不过这个回答提醒我们，就是要求罗素悖论中导致悖论的集合需要预先证明其存在性。

　　以上提到的说谎者悖论、罗素悖论、理发师悖论都有一个共同点，就是都存在“自指”。自指除了在单个命题内实现，还可以是跨命题的，例如以下“扩展的”说谎者悖论：

　　“下面这个句子是假的。

　　上面那个句子是真的。”

　　解决罗素悖论的方法看起来很简单，即通过分类的方法将导致悖论的集合排除出讨论范围。具体而言是这样的(以下摘录书中原话)：有一个"类型"最低的集合，只能包含"对象"而不是集合做元素。高一层类型的集合，只能包含对象或最低类型的集合。一般的说，一个给定类型的集合只能包含对象或类型低于它的集合。每一个集合都属于一个特定的类型。很清楚，没有一个集合可以包含自己，因为，包含它的集合得属于比它更高的类型。在这样的系统中只能有"普通的"集合。此外，前面提到的所有普通的集合的集合不再被看作是一个集合了，因为它不属于任何一个有穷类型。至于说谎者悖论，尽管分类法无法解决，还是能通过引入“层次结构”来解决。这种“解决方案”在我看来毫无说服力，完全就是在逃避问题。

3

　　逾两千五百年后，逻辑学家哥德尔提出了著名的哥德尔定理(在此特指“哥德尔不完备定理”)，它也包含了一个怪圈。该定理在书中的表述是这样的：

　　“数论的所有一致的公理化形式系统都包含有不可判定的命题。”

　　“All consistent axiomatic formulations of number theory include undecidable propositions.”

　　在维基百科上，对“哥德尔不完备第一定理”的表述为：

　　“任何兼容的形式系统，只要蕴涵皮亚诺算术公理，就可以在其中构造在体系中不能被证明的真命题，因此通过推演不能得到所有真命题（即体系是不完备的）。”

　　“Any consistent formal system F within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are statements of the language of F which can neither be proved nor disproved in F.”

　　其中，“皮亚诺算术公理”指的是皮亚诺提出的关于自然数的五条公理，由此可以建立一阶算术系统：

1. 0是自然数；
2. 每一个确定的自然数a，都有一个确定的后继数a' ，a' 也是自然数（一个数的后继数就是紧接在这个数后面的数，例如，0的后继数是1，1的后继数是2等等）；
3. 对于每个自然数b、c，b=c当且仅当b的后继数=c的后继数；
4. 0不是任何自然数的后继数；
5. 任意关于自然数的命题，如果证明了它对自然数0是对的，又假定它对自然数n为真时，可以证明它对n' 也真，那么，命题对所有自然数都真。（这条公理即数学归纳法）

　　皮亚诺公理在数学分析课上已有接触，它定义了自然数(注：这一公理根据自然数是否包括0可稍作调整)。哥德尔不完备定理则是在阅读本书时才第一次听说的，它让我非常震惊(尽管书中声称“我们的文化已经把哥德尔定理连同相对论和量子力学等观念上的革命一起吸收了”)，引入算术的一阶谓词逻辑系统竟然会有一些命题既不可被证实也不可被证伪，我的第一个想法就是自然科学很可能不是万能的，因为从直观上形式逻辑的命题系统肯定强于自然科学的命题与公理系统。接受十余年的基于无神论，以数理化生为核心的教育后，我(此前)想当然地认为没有什么是自然科学解释不了的，如果有，那就是科学家还没研究出来。现在想到中物理学中尚且随处可见唯象理论(包括牛顿力学、量子力学、相对论等等，实际上整个物理学究其根本都是唯象的，毕竟没有人能解释诸如为什么万有引力的大小、电荷力的大小与距离呈的是-2次方的关系之类的问题)，化学领域更是充满了规则与例外，我越发觉得自然科学不过是发展了一套解释世界的语言，但是从未触及世界的本源：时间起点的世界，是什么提供了源动力，以及物理法则之上的制定者是谁等等。我们似乎又回到了形而上和宗教的疆域。毫无疑问，哥德尔不完备定理令尚在自然科学研究初期阶段的小朋友非常绝望。

　　另见文章称，现代计算机在数学上是与图灵机等价的，这使得有的算法无法确定能否在有限时间内运行完毕。进一步地，根据哥德尔不完备定理推论，我们认为在现代计算机的框架上不可能实现强人工智能。(注：此观点将在后续的读书笔记中再次讨论)

　　补充一点前言中没有提到的哥德尔完备性定理，在维基百科上的表述为：

　　“在一阶谓词演算中所有逻辑上有效的公式都是可以证明的。”

　　“We first fix a deductive system of first-order predicate calculus, choosing any of the well-known equivalent systems. Gödel's original proof assumed the Hilbert-Ackermann proof system. The completeness theorem says that if a formula is logically valid then there is a finite deduction (a formal proof) of the formula.”

　　通过对比不难发现，这两个定理合在一起在说一阶谓词系统本身是完备的，但引入算术之后(仍然是一阶谓词系统)就有些命题不可证实也不可证伪。

4

　　前3节的内容写于2019年3月。彼时，我看到有人在反对哥德尔不完备定理的论述中称哥德尔并没有提出具体的什么定理是不可证的(相关网页目前找不到了)。这确实是错误的说法，然而哥德尔的原始论文又是德语写成的，让人很难找到这个不可证的命题在哪里。经过一段时间的搜索，我当时也确实未找到有什么具体定理是不可证的。随着毕业进程的临近，此事也被一再搁置。直到2019年11月左右，我看到“学术状态帝”在微博上提到哥德尔定理也是民科重灾区，甚至不只是民科，许多经受过自然科学知识训练的人在没有完全了解哥德尔定理的证明过程与适用范围的情况下都会做出错误的延伸与判断。这促使我再次进行相关内容的搜索与学习。事实上中文互联网上早已出现了一些足够简单的介绍，让我们有机会了解到这个不可证的命题是什么以及其中证明哥德尔不完备定理涉及的思想。(混乱博物馆, 《哥德尔证明》PDF)

　　这个不可证命题的形式与说谎者悖论极其相似：

这个命题是不可证的。

　　要证明这个命题存在且不可证，哥德尔首先引进了哥德尔数的概念，巧妙地将命题转化为了自然数，步骤如下：

1.将一个命题中的各个符号指定一个数；

Figure 3. 一种可能的符号与数字的对应方式。请注意，利用0和后继s，可以代表任意的自然数，如2可以用ss0表示。

2.将命题产生的数依次作为质数序列的幂，将它们相乘，即得到哥德尔数，例如：

Figure 4. 命题“存在数自然数x, 使得x是自然数y的后继”与其对应的哥德尔数。

　　通过这个规则，我们可以唯一确定一个给定形式命题所对应的哥德尔数；反过来通过因式分解，可以将一个哥德尔数唯一地转化成一个对应的命题。并且，所有的命题都有其对应的哥德尔数。

　　利用哥德尔数，我们可以把一个“元数学命题”转化为“数学命题”。例如，元数学命题“¬ (0=0)是一个表达否定的命题”，可以看到否定符号¬对应数字1，该符号是命题的第1个符号，对应质数2，转化为数学命题，即“哥德尔数2¹×3⁸×5⁶×7⁵×11⁶×13⁹可被2¹的整除而不能被2²整除”。由这个例子可以看到一个逻辑问题变成了一个数字关系的问题。

　　有了哥德尔数，接下来就该利用它来构造自指了。构造一个命题G₁，

G₁: ¬(∃x) Dem(x, g)

　　它说“不存在一个x，使得证明哥德尔数为x的公式的过程可以证明哥德尔数为g的公式”，相当于说“不存在一个证明过程可以证明哥德尔数为g的公式”，即“哥德尔数为g的公式不可证”。作为引理，哥德尔证明了Dem(x, z)是系统中的一个公式。请注意，x应当是一个变量，g应当是一个常量，即一个确切的数字。为了找到一个g，下面将构造一个公式。

　　接下来，我们定义一个替换函数，

Sub(y, 17, y)

　　将这个公式的变量从左往右读，它代表一个数，这个数等于“在一个哥德尔数为y的公式中，将哥德尔数为17的变量替换为数值y后，所得到新公式的哥德尔数”。特别注意，Sub代表一个数，而不是一个命题，在计算哥德尔数时，它等价于sss…ss0，s的数目等同于替换所得新公式的哥德尔数。这一步骤很容易让人疑惑，Sub函数又是此构造的核心，需要反复思考。

　　现在，我们将G₁的g代替为这个替换函数，得到了命题G₂，

G₂: ¬(∃x) Dem(x, Sub(y, 17, y))

　　前面我们强调，g应当是一个常数，现在Sub(y, 17, y)是一个关于y的函数，使得替换函数所代表的数也是变量而不是常数，这导致G₂不是一个固定的公式。解决办法很简单，作为系统中的公式(不是固定的也没有关系，任取一个)，G₂必定具有可计算的哥德尔数，在此记为n，替换掉原先的变量y，此时得到我们所需要的命题G：

G: ¬(∃x) Dem(x, Sub(n, 17, n))

　　现在n是一个常数，写成0的后继的形式即sss…ss0，s的个数等于n的数值。这样，G的哥德尔数确定下来，并形成自指，即公式G说哥德尔数为g的公式(即Sub(n, 17, n))不可证，同时G的哥德尔数恰等于g。命题构造完成。

　　很可能你并没有完全理解前面所述的两次替换，并疑惑于为什么由此构造的公式G的哥德尔数恰好与Sub(n, 17, n)相同。在此再次强调，Sub(n, 17, n)代表一个数，而不是一个命题。我们参照一下前文Sub(y, 17, y)的定义，写出Sub(n, 17, n)所代表的数：

“在一个哥德尔数为n的公式中，将哥德尔数为17的变量替换为数值n后，所得到新公式的哥德尔数。”

　　对照G₂到G的生成过程：

“公式G₂的哥德尔数是n，将G₂中所有哥德尔数为17的变量替换成n，得到新公式G。”

　　显然，“新公式”G的哥德尔数与Sub(n, 17, n)所代表的数相等。

　　综上，构造的公式G的语义即为“公式G不可证”。由简单的反证法，假设G可证，则“G可证”与“¬(G可证)”同时为真，违反了一致性的原则(命题与命题的否定不能同时为真)，而G又是这个逻辑系统的一个公式，可以得到这个逻辑系统不完备的结论。哥德尔在其论文中确定了“这个逻辑系统”指的是含有皮亚诺算术的形式系统，即哥德尔不完备定理：

任何兼容的形式系统，只要蕴涵皮亚诺算术公理，就可以在其中构造在体系中不能被证明的真命题，因此通过推演不能得到所有真命题（即体系是不完备的）。

　　注意这里提到“推演不能得到所有真命题”，前文构造的G也是一个真命题，但是它的正确性不能在这个逻辑系统中得证。

5

　　除了哥德尔在证明的过程中构造的G，在实际的一阶谓词逻辑系统中，有没有类似的定理是不可证的呢？这同样是一个难以检索的问题。后来我在b站找到一个视频(av31411706)，里面提到几个这样的例子，包括Goodstein定理、选择公理、连续统假设。以下简单介绍一下Goodstein定理的内容。（由于看不懂Goodstein定理的证明以及Goodstein定理无法在皮亚诺算术系统中证明的证明，在此略过）

       首先要给出一个Goodstein序列。对于一个自然数，在此以35为例，将其写成二进制的形式：

35₍₁₀₎ = 100011₍₂₎ = 2⁵+2+1

       括号内数字代表进制数。注意到指数项上的5比2要大，再将它进一步写成2²+1，即

　　如果在得到的表示中，指数中的指数仍有比2大的数，则继续迭代，直至没有比2大的数为止。现在，我们知道100和19分别可以写作：

100 = 3³⁺¹+2×3²+1

　　现在以19为例，构建一个Goodstein序列。令序列的第1项为19，

　　Goodstein序列的第2项将第1项所有的数字2改为3，最后减1，

　　类似地，第3项中把所有的数字3改为4，最后减1，

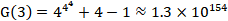
　　以此类推，即得到Goodstein序列。尽管看起来数列将以极快的速度发散，Goodstein定理告诉我们：无论起始的自然数为多少，Goodstein数列总是能收敛到0。

6

　　现在我们回过头来讨论第3节中标红的观点：根据哥德尔不完备定理推论，我们认为在现代计算机的框架上不可能实现强人工智能。这个判断的依据是停机问题，即不存在一个程序P，对于任意输入的程序w，能够判断w会在有限时间内结束或者死循环。但是强人工智能的实现，真的与停机问题有很大的关联吗？据说侯世达写作GEB的目的之一就是回击强人工智能不可实现的观点。抛开GEB尚未阅读到的部分，我在此给出一个当前对此问题的判断。这个判断可能随着今后学习到更多知识而有所变化，正如我从第一次听闻哥德尔不完备定理后对其证明了强AI不可实现深以为然到如今的转变一样。

　　强人工智能亦称为通用人工智能，指的是具有一类强泛化能力的计算机程序。稍微了解过机器学习的同学们都知道它从根本上不同于当前基于机器学习的人工智能，机器学习本质上是机器在做一堆人为规定好的数学运算，与智能或者自我意识都完全不搭边。与其担忧人工智能是否会毁灭人类，不如关心一下制造出强人工智能本身是否可能。从停机问题出发否定强人工智能的可能性，在于当前的计算机体系是图灵等价的，一个图灵机总会遭遇某些问题无法判定，同时我们还在直觉上认为人脑的思维模式比计算机更优越(例如人脑可以理解高阶谓词逻辑，而计算机只能运行在一阶谓词逻辑上)。然而在可计算理论中，人脑的计算模型并不强于图灵机，同样地在停机问题上认为人类就比计算机更优越是不正确的，因为计算机无法判定的问题，人类同样无法判定。或许黎曼猜想就是一个在现有数学框架下无法得证的问题，我们假定这个猜想确实是不可证的，那么现在的情况是，计算机证不出来，人类也证不出来，也就是说在黎曼猜想的问题上人类并不比计算机更优越。如果人类的计算能力不强于计算机，有什么理由认为强人工智能不可实现呢?

　　以上判断更像是综述，综合了一些我当前认同的观点。这些观点的依据往往是难以理解的或者不充分的，由此若产生判断上的偏差，在所难免。记录与此的目的，是将这些观点作为建立认知的基础，鼓励自己在不断的学习中去伪存真。

7

三部创意曲

　　在GEB的每个章节之间还有一段对话体的“插曲”，这些插曲的主角正是古希腊哲学家芝诺以及他所提出的悖论中的阿基里斯与龟。阿基里斯(Achilles, 另译“阿喀琉斯”)在希腊神话中是一名飞毛腿，是世界上跑得最快的人。芝诺提出了几个悖论，其中一个阿基里斯悖论如下：

　　(阿基里斯在后面追逐龟，)龟不会被阿基里斯追上。由于阿基里斯首先应该达到龟出发之点，此时龟已经往前走了一段距离。因此龟总是在阿基里斯前面。

　　类似地，还有二分法悖论：

　　运动是不可能的。由于运动的物体在到达目的地前必须到达其半路上的点，若假设空间无限可分则有限距离包括无穷多点，于是运动的物体会在有限时间内经过无限多点。

　　以及飞矢不动悖论：

　　一支飞行的箭是静止的。由于每一时刻这支箭都有其确定的位置因而是静止的，因此箭就不能处于运动状态。

　　如今，借助极限与微积分的概念，这些悖论都非常容易反驳，从哲学问题变成了简单的数理问题。对于阿基里斯悖论，将阿基里斯与乌龟的距离写作成随时间变化的序列，这个序列将会收敛到0，即阿基里斯可以在有限的时间内追上乌龟。二分法悖论与之类似，即使认可空间无限可分，空间中无穷多个点之间的距离之和却不必然是无穷大的。飞矢不动悖论则直接否认运动是物体位置随时间变化的。

8

　　本节插曲主要只介绍了主人公以及芝诺的几个著名的悖论，而阿基里斯与乌龟的赛跑还未正式开始。如果我们的读书笔记到此为止，篇幅也过于短小。正巧，前段时间已经结课的材料化学课程群里，有位同学转发了一篇批驳微积分原理的文章，点开一看，作者名写着“丁小平”。他曾经被北京大学数学文化研究会(学生社团，事后被勒令整改，中止活动)邀请，原计划在2016年5月10日在二教做题为《对现行微积分原理的反思与数学科学发展的转折》的报告，而不少同学认为丁是民科并在bbs上发帖抗议，在他们的强力反对下未能成行。在此，我们借由他的观点，稍稍延续此次讨论。

　　丁小平最广为人知的一篇文章应该是《浅谈现行微积分原理的错误》(链接：知网，豆瓣搬运) 。或许你并没有兴趣去阅读丁发表在《前沿科学》上的这篇“论文”，或者读完并不清楚他主要想表达什么观点，在此总结一下，他的核心观点是“dx = Δx是错误的”，文中其它的进一步的论述都基于这一基本观点。某种程度上说，丁的核心观点是正确的，但这个观点丁绝不是第一个提出来的。早在1734年，乔治·贝克莱主教就提出了对微积分的质疑。在求x²的导数时先取一个不为0的增量Δx，由Δy=(x + Δx)² - x² 得到 2xΔx+Δx²，除以Δx，得2x+Δx，然后令Δx为0，所以得到结果为2x。贝克莱指出先取一个不为0的增量Δx, 后又令Δx为0，那么Δx到底是不是0呢？

　　“它们既非有限量，也不是无限小的量（即，比任何有限量都小的量），然而却又不是零。那么我们或许也只好称其为‘消逝量的幽灵’了吧？” (参考来源) 这一质疑与“dx≠Δx”是等价的，而这个问题导致了第二次数学危机。神奇的是，尽管dx与Δx的问题一直没有在数学上得到解决，运用牛顿-莱布尼兹公式却在实践中一次又一次得到正确的积分结果。这场数学危机最终在数学分析被建立起来后得到完美的解决。数学分析的核心是ε-δ语言，最早于1817年由波尔查诺提出，并由魏尔施特拉斯完善。ε-δ语言对极限进行了严格定义，学过数分的朋友们肯定不会把丁的观点放在心上，因为那些问题有了数学分析的方法之后就不再重要了。

9

　　在此，向没有学过数学分析的朋友们简单介绍一下处处体现着数学之美的ε-δ语言。

　　首先，从一个数列{x_n}开始说起。用ε-N语言来描述数列{x_n}会在n→∞的时候收敛到a：

∀ ε > 0, ∃ N∈N₊, ∀ n > N, | x_n - a | < ε

对于任意给定的正实数ε，都存在一个正整数N, 使得所有大于N的整数n都满足x_n与a的差值小于ε

　　反过来，用ε-N语言说数列{x_n}发散：

∃ ε > 0, ∀ N∈N₊, ∃ n > N, | x_n - a | > ε

存在某个正实数ε，对所有正整数N, 都能找到一个大于N的整数n，使得x_n与a的差值大于ε

　　一个简单的例子，用ε-N语言证明数列x_n = 1 / n收敛到0：

对于任意的ε，存在整数N > 1 / ε，使得所有n > N即n > 1 / ε，满足| x_n - 0 | = 1 / n < ε。

　　特别地，对于ε = 0.0001，存在N = 10001，使得所有n > N即n > 10001, 满足| x_n - 0 | < 1/10001 < 0.0001。

　　现在我们可以进行类推，用ε-δ语言来讨论一个函数f(x)，如果f(x)在x → x₀时趋于一个值a，那么

∀ ε > 0, ∃ δ > 0, ∀ 0 < | x - x₀ | < δ, | f(x) - a | < ε

　　无穷极限的写法稍有变化，若f(x)在x → ∞时趋于一个值a，那么

∀ ε > 0, ∃ Δ∈R, ∀ x < Δ, | f(x) - a | < ε   (Δ-ε定义)

　　若f(x)在x → x₀时趋于无穷大，那么

∀ E > 0, ∃ δ > 0, ∀ 0 < | x - x₀ | < δ, | f(x) | > E   (δ-E定义)

　　最后，我们看一下ε-δ语言如何描述积分。我们先引入“有限和”的概念。将函数f的积分区间[a, b]分割为有限个有限大的区间，区间的边界点依次记为x₀, x₁, …, x_i, …, x_N, (其中x₀ = a, x_N = b)记为分割P，分割的模|P|即最大区间的大小，即P = max{Δx_i}，每个区间选取标志点ξ_i, 其中x_i-1 < ξ_i < x_i，得到标志点组{ξ_i}。现在可以定义有限和σ：

σ(f, P, ξ) = Σ_i f(ξ_i) Δx_i

　　很自然地想到，如果|P|趋近于0，有限和就趋近于积分和。结合ε-δ语言，我们就得到了黎曼可积的定义：函数f在[a, b]上有定义，若∃ I∈R, 对∀ ε > 0, ∃ δ > 0, 使得对于所有满足|P| < δ的分割P都有 | σ(f, P, ξ) - I | < ε，则f在[a, b]上可积，其定积分为I，记为。