RANSAC简史（一）——RANSAC之初

在开始正式的介绍之前，先做一个简单的定义，以免产生歧义：

1、本文中的“数据点”是指：

1）对于直线拟合、平面拟合等问题，即为相应的二维/三维坐标点；

2）对于从匹配点中估计基本矩阵、单应矩阵等问题，即为一对匹配点坐标级联组成的向量。

一、RANSAC之前

RANSAC在1981年被Martin A. Fischler and Robert C. Bolles两人提出，以解决给定点集的模型估计问题。在现实应用中，我们经常遇到的情况是：给定的点集中存在错误的点。传统的模型估计方法，大都采用所有的点进行模型最小二乘的拟合，这种方法往往容易受野点影响而得到错误结果（相当于陷入局部最优）。该最小二乘法的一种变种是，首先用所有点估计模型，而后剔除误差较大的点，而后再次估计模型，以此迭代。然而，由于野点的影响，往往会导致最开始估计的模型不准确，从而导致正确的点被剔除掉，最终导致模型估计的失败。下面是一个例子：

 

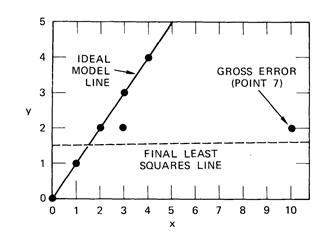
由于点7的影响，导致正确的点被剔除，最终拟合的直线为虚线，而不是正确的实线。

二、RANSAC之1.0版本

RANSAC方法为第一个方法，采用最少能决定模型的点进行模型估计的方法，最原始的方法被描述为：

 

 

整个算法被分为三步：

1） 从所有的数据中采样n个点，以能确定出模型；

2） 利用采样点计算模型；

3） 利用模型来确定其他点是否是内点；如果内点率达到指定值，算法终止，并用所有内点优化模型；否则，继续上述过程，直到达到指定的迭代次数，此时将最高内点率对应的模型作为最终模型。

上述思路简洁明了，其核心思想就是：待求解的模型，应该是能同时使最多数据点都符合模型。从这一思想从发，其实可以有另一条不同的思路，后续我会进一步介绍。

三、RANSAC 1.0版本剖析

下面让我们回顾下该方法，看该方法在具体应用中，还需要解决哪些问题：

算法第一步，从数据中采样n个点，这里要求n为能确定模型的最小的数据量，那么该选取怎样的采样准则？从所有数据中采样，还是仅仅从部分数据（总数据的一个子集）中进行采样？每个数据被采集的可能性是否相同？采取随机采样，还是按一定顺序进行采样？是否需要避免同一组数据被重复采样，如果需要，该如何避免？这里先给出通常的做法，更加细致的分析也留到后续。通常情况下，我们在所有数据中进行随机采样，且所有数据每次被采样的可能性是一样的，而且我们通常不考虑两次采样得到的样本是重复的。

算法第二步，利用采样数据计算模型。我们知道，在第一步中，我们要求采样点尽可能少，同时我们也知道，当数据点存在噪声（通常考虑为高斯噪声）时，样本点的数目越多，求解的模型越准确。这就意味着我们此刻求解的模型不够准确，那么这个不够准确的模型，是否能够用来判断其他点是否是内点？其次，如果我们待求解的问题，无法用一个模型，或者无法用一个仅包含若干个参数的模型进行表达，此时是否还能使用“最大一致性”的思路？针对第一个问题，我们通常认为虽然模型存在误差，但是在后续内点判断中，我们设定一定的误差阈值，因此能够用该模型来近似最终模型。同时，一些RANSAC的改进，采用“局部优化”技术来一定层度解决这一问题，关于该方法的讨论，同样会在后续，进行详细的剖析。针对第二个问题，有一些无模型的“最大一致性估计”方法，同样也留待后续介绍。

算法第三步，首先，利用求解的模型确定其他点是否为内点。一个重要的问题是，如何判断其他点是否为内点？通过其他点与模型的符合程度？那么如何设置这样一个阈值？有时一个数据是否为内点（例如两个数据点相冲突，不可能同时为内点。这种情况会发生在：根据两张图特征点匹配，求解其基础矩阵时，如果A图中的两个点，匹配到B图中的同一个点），还与其他数据相关，那么此时如何考虑数据间的关联？

其次，“如果内点率达到指定值，则终止算法”，那么如何设置这样一个阈值？因为对于一组数据，通常情况下我们是无法知道其最大内点率。（但问题也不是绝对，我们也可以事先求解出最优模型对应的内点率。哈哈，是不是很crazy，这也留待后续的剖析。）因此，这一迭代的终止条件，现在的RANSAC算法中，已经很少见了。我们通常采用一定置信度下，达到能够保证至少一次所有的采样点都为内点的最少采样次数，作为终止条件。

最后，如何确定最少的采样次数。原文中提出了两种方案。假设在一次采样中，所有点都为内点的概率为p，那么“所有采样点都为内点首先发生在第k次采样”这一事件服从几何分布（参考射击时第k次才命中这一问题），于是：

 

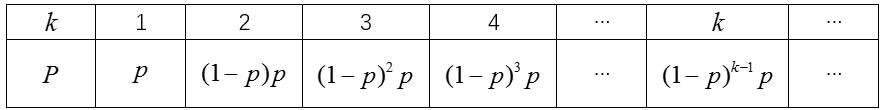
原文方案一：求解k的期望值和方差，采用期望值加上2到3倍方差，作为采样次数。这种方案，可以理解为求解分布的“上分位数”，以保证以一定“所有采样点都为内点”在进行k次采样后发生过。

原文方案二：如果要求第 次采样后，至少一次“所有采样点都为内点”的概率大于 那么：

由此，

 

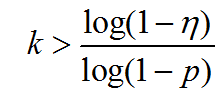
这里一次采样中所有点都为内点的概率为：

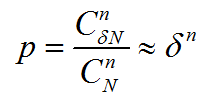
其中N为总数据量，n为最小采样数，为内点率。

在此，我们可以看出，为什么选取最少的样本点进行模型估计。因为，采样量每增加1，对应需要进行的采样次数就增加很多，尤其是在内点率很低的情况下，这种情况尤其严重。

 

写到这里，我们已经对RANSAC最初版本进行了详细的介绍，同时我们很具体剖析了其各个步骤可能面临的问题。针对这些问题，后续衍生出了很多RANSAC的变种，我们将在后续进行具体的介绍。

 

参考文献：

[1]   Fischler M A . Readings in Computer Vision || Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Readings in Computer Vision, 1987:726-740.