2020微软笔试题

1.将N个数字划分成N/K组，每组K个数字，每组中的数字互不相同，求每个子数组最大最小元素的差值之和的最小值。

输入：

N=12, K=4

arr=3,3,4,4,5,5,6,6,8,8,10,10

输出：

15

{3,4,5,6} 6-3=3

{3,4,8,10} 10-3=7

{5,6,8,10} 10-5=5

3+7+5=15

思路：先对数组从小到大排序，统计重复数字出现最多的个数，如果大于N/K的话，不能划分，直接返回0。

然后枚举每一种情况，dfs+剪枝。

int ans = Integer.MAX_VALUE;

public int solve(int N, int K, int[] arr) {
    Arrays.sort(arr);
    Map<Integer, Integer> map = new HashMap<>();
    int dup_max = 0;
    for (int i = 0; i < arr.length; i++) {
        map.put(arr[i], map.getOrDefault(arr[i], 0) + 1);
        dup_max = Math.max(dup_max, map.get(arr[i]));
    }
    //重复数字出现最多的个数，如果大于N/K的话，不能划分，直接返回0
    if (dup_max > N / K) {
        return 0;
    }
    int[] num = new int[N];
    int[] flag = new int[N];
    //用于判断分组中的重复元素
    Set<Integer> set = new HashSet<>();
    helper(N, K, 0, arr, num, flag, set);
    return ans;

}

//dfs + 剪枝
public void helper(int N, int K, int index, int[] arr, int[] num, int[] flag, Set<Integer> set) {
    //index==N,说明分组完毕，计算每个子数组最大最小元素的差值之和
    if (index == N) {
        int res = 0;

        for (int i = 0; i < num.length; i += K) {
            int min = Integer.MAX_VALUE;
            int max = Integer.MIN_VALUE;
            for (int j = i; j < i + K; j++) {
                min = Math.min(min, num[j]);
                max = Math.max(max, num[j]);
            }
            res += Math.abs(max - min);
        }

        if (res < ans) {
            ans = res;
            for (int i = 0; i < num.length; i++) {
                System.out.print(num[i] + " ");
            }
            System.out.println();
            System.out.println(res);
        }

        return;
    }


    for (int i = 0; i < N; i++) {
        //剪枝
        if (flag[i] == 0) {
            if (set.contains(arr[i])) {
                continue;
            }
            set.add(arr[i]);
            flag[i] = 1;
            num[index] = arr[i];
            if ((index + 1) % K == 0) {
                set = new HashSet<>();
            }
            helper(N, K, index + 1, arr, num, flag, set);
            set.remove(arr[i]);
            flag[i] = 0;
            num[index] = 0;

        }
    }
}

2.给一个字符串，每次可以移除其中一个字符，或者移除一个回文子串，求 全部移除所需最少次数

例如：1，4，3，1，5. 先移除 3，再移除 1 4 1，再移除 5，得到最少次数 3.

leetcode原题：https://leetcode.com/problems/palindrome-removal/description/

题解：https://coordinate.wang/index.php/archives/2737/

两种情况：

1. 直接删除
2. 找到该字符串对应的回文串，再删除

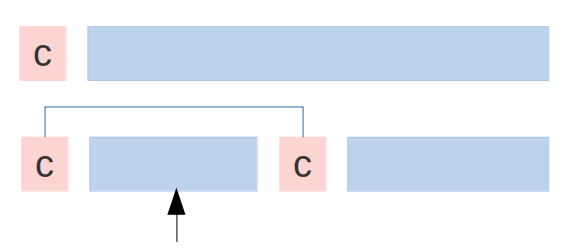
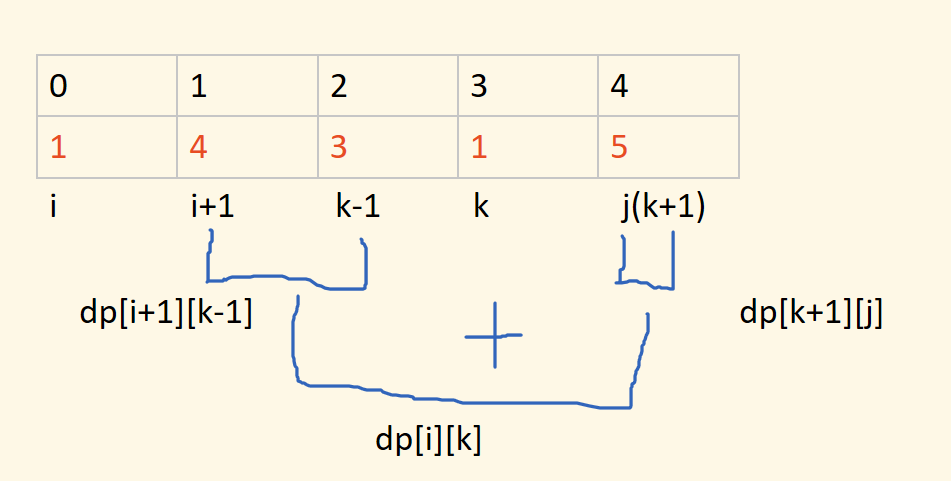
i+1==k考虑回文子串长度为空的情况

//动态规划。在原来题解的基础上，加了注释。
public static int minimumMoves(int[] arr) {
    int n = arr.length;
    //dp[i][j]表示删除从i到j的数字所需的最少操作次数
    int[][] dp = new int[n + 1][n + 1];
    //l表示当前数字的长度
    for (int l = 1; l <= n; l++) {
        int i = 0, j = l - 1;
        while (j < n) {
            if (l == 1) {
                //base，每个数字的删除次数为1
                dp[i][j] = 1;
            } else {
                //不考虑回文子串的情况下，删除次数为之前的删除次数+1
                dp[i][j] = 1 + dp[i + 1][j];
                //考虑回文子串
                for (int k = i + 1; k <= j; k++) {
                    if (arr[i] == arr[k]) {
                        //更新dp[i][j]
                        dp[i][j] = Math.min(dp[i][j], dp[i + 1][k - 1] + dp[k + 1][j] + (i + 1 == k ? 1 : 0));
                    }
                }
            }
            i++;
            j++;
        }
    }
    return dp[0][n - 1];

}

3.给一个无向图，N个顶点，M条边，0为起点，N-1为终点，每条边初始权值为 1。图中除普通节点外有 4 种节点。

第一种：走过这种节点后的两条边权值翻倍(Sand)

第二种：走过这种节点后的两条边权值减半 (Nitro)

第三种：走到这个节点就停止，不能再走了(Cop)

第四种：走到这个节点，下一条边的权值+1(Crash)

求节点 0 到 N-1 的最短权值和路径。

类似于图的深度优先遍历，需要进行回溯

//Path记录起点到终点的路径path和花费cost
class Path {
 List<Integer> path;
 double cost;

 public Path(List<Integer> path, double cost) {
     this.path = path;
     this.cost = cost;
 }
}

//存储最短路径
Path minPath = new Path(new ArrayList<>(), Integer.MAX_VALUE);

public int[] minTimes(int city, String[] strs, int road, int[][] arr) {
 Map<Integer, Set<Integer>> map = new HashMap<>();
 for (int i = 0; i < arr.length; i++) {
     Set<Integer> set;
     if (!map.containsKey(arr[i][0])) {
         set = new HashSet<>();
     } else {
         set = map.get(arr[i][0]);
     }
     set.add(arr[i][1]);
     map.put(arr[i][0], set);
 }
 Path path = new Path(new ArrayList<>(), 0);

 dfs(0, city - 1, strs, map, path);

 int[] res = new int[minPath.path.size()];
 for (int i = 0; i < res.length; i++) {
     res[i] = minPath.path.get(i);
 }
 return res;

}
//计算起点到终点的花费
public double cal(String[] strs, Path path) {
 double res = 0;
 int size = path.path.size();
 double[] cost = new double[size - 1];
 Arrays.fill(cost, 1);
 for (int i = 0; i < size; i++) {
     if (strs[path.path.get(i)].equals("Nitro")) {
         if (i < size - 1) {
             cost[i] *= 0.5;
         }
         if (i + 1 < size - 1) {
             cost[i + 1] *= 0.5;
         }

     } else if (strs[path.path.get(i)].equals("Sand")) {
         if (i < size - 1) {
             cost[i] *= 2;
         }
         if (i + 1 < size - 1) {
             cost[i + 1] *= 2;
         }

     } else if (strs[path.path.get(i)].equals("Crash")) {
         if (i < size - 1) {
             cost[i] += 1;
         }
     }

 }

 for (int i = 0; i < cost.length; i++) {
     res += cost[i];
 }
 return res;

}
//图的深度优先遍历
public void dfs(int begin, int end, String[] strs, Map<Integer, Set<Integer>> map, Path path) {
 if (begin == end) {
     path.path.add(end);
     double cost = cal(strs, path);
     if (cost < minPath.cost) {
         // 一定要使用new ArrayList<>(path.path)。
         // 直接传入path.path，会导致返回的minPath.path为空，这是由于Java的值传递导致的。
         minPath = new Path(new ArrayList<>(path.path), cost);
         //                System.out.println("cost:" + cost);
         //                System.out.println("minPath" + minPath.path.toString());
     }
     //回溯
     path.path.remove(Integer.valueOf(end));

     return;
 }

 Set<Integer> set = map.get(begin);
 //寻找下一个可访问的节点
 for (int nextCity : set) {
     if (path.path.contains(nextCity) || strs[nextCity].equals("Cop")) {
         continue;
     }
     path.path.add(begin);
     dfs(nextCity, end, strs, map, path);
     //回溯
     path.path.remove(Integer.valueOf(begin));

 }

}

测试用例：

Test1:
 int city = 5;
 int road = 5;
 String[] strs = {"None", "Cop", "None", "None", "None"};
 int[][] map = {{0, 1}, {0, 2}, {1, 2}, {2, 3}, {3, 4}};

 result：{0,2,3,4}

Test2:
 int city1 = 7;
 int road1 = 8;
 String[] strs1 = {"None", "Cop", "Sand", "None", "Nitro", "None", "None"};
 int[][] map1 = {{0, 1}, {0, 2}, {1, 2}, {2, 3}, {2, 4}, {3, 6}, {4, 5}, {5, 6}};

 result：{0,2,4,5,6}