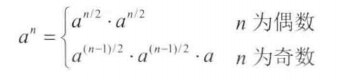剑指offer题解(完结)
### 3-1 数组中重复的数字

每遍历数组中的一个数字,就让其归位(放置在正确的数组下标)。当在归位的过程中,发现该数组下标所存放的数字和当前要归位的数字相同时,则发生了重复,返回该数字。
空间复杂度O(1),时间复杂度O(n)。
public class FindDuplicateNum_3 {
public static boolean findDuplicateNum(int[] arr, int length, int[] dup) {
if (arr == null || length <= 0) {
return false;
}
//时间复杂度O(n)
for (int i = 0; i < length; i++) {
//每个数字最多交换2次
while (arr[i] != i) {
if (arr[i] == arr[arr[i]]) {
dup[0] = arr[i];
return true;
}
swap(arr, i, arr[i]);
}
}
return false;
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
3-2 不修改数组找出重复数字

空间复杂度O(1),采用类似二分查找的算法,时间复杂度O(nlogn)。
思路:将1~ n上的数字划分成两块:1~ m和m+1~ n,然后统计数组中该区间上的数字个数,如果数字个数大于区间长度,则发生了重复,然后在该区间上继续二分,直至区间长度等于1。
//不修改数组找出重复数字
public static int findDuplicateNumNoEdit(int[] arr, int length) {
if (arr == null || length <= 0) {
return -1;
}
int start = 1;
int end = length - 1;
while (start <= end) {
int mid = start + ((end - start) >> 1);
int count = getCount(arr, length, start, mid);
//System.out.println(mid+" "+count);
if (start == end) {
if (count > 1) {
return start;
} else {
return -1;
}
}
if (count > (mid - start + 1)) {
end = mid;
} else {
start = mid + 1;
}
}
return -1;
}
private static int getCount(int[] arr, int length, int start, int end) {
int count = 0;
for (int i = 0; i < length; i++) {
if (arr[i] >= start && arr[i] <= end) {
count++;
}
}
return count;
}
4 二维数组查找

从左下或者右上角开始查找,每次判断可以剔除一行或者是一列,时间复杂度O(n+m)
public static boolean Find(int target, int[][] array) {
/*左下查找*/
int rows = array.length;
if (rows == 0) {
return false;
}
int columns = array[0].length;
if (columns == 0) {
return false;
}
int column = 0;
int row = rows - 1;
//注意数组边界
while (row >= 0 && column < columns) {
if (target == array[row][column]) {
return true;
} else if (target < array[row][column]) {
row--;
} else {
column++;
}
}
return false;
}
5 替换空格

先统计出字符串中的空格数量,然后计算出替换后的字符串长度,从后往前遍历字符串,依次填充。
public static String replaceBlankSpace_2(String str) {
if (str == null) {
return null;
}
char[] chars = str.toCharArray();
int count = 0;
for (int i = 0; i < chars.length; i++) {
if (chars[i] == ' ') {
count++;
}
}
int newLength = chars.length + (count << 1);
int p1 = chars.length - 1;
int p2 = newLength - 1;
char[] newChars = new char[newLength];
while (p1 >= 0) {
if (chars[p1] == ' ') {
newChars[p2--] = '0';
newChars[p2--] = '2';
newChars[p2--] = '%';
p1--;
} else {
newChars[p2--] = chars[p1--];
}
}
return String.valueOf(newChars);
}
6 从尾到头打印链表

使用栈,遍历一遍链表,将链表中的节点压栈,然后输出栈中的节点
import java.util.Stack;
public class FromHeadtoTailPrintLinkedList_6 {
static class ListNode {
int key;
ListNode next;
public ListNode(int key) {
this.key = key;
}
}
public static void fromHeadtoTailPrintLinkedListByStack(ListNode head) {
if (head == null) {
return;
}
Stack<ListNode> stack = new Stack();
while (head != null) {
stack.push(head);
head = head.next;
}
while (!stack.isEmpty()) {
System.out.print(stack.pop().key + " ");
}
}
public static void fromHeadtoTailPrintLinkedListByRecursion(ListNode head) {
if (head == null) {
return;
}
fromHeadtoTailPrintLinkedListByStack(head.next);
System.out.print(head.key + " ");
}
public static void main(String[] args) {
ListNode head = new ListNode(0);
head.next = new ListNode(1);
head.next.next = new ListNode(2);
head.next.next.next = new ListNode(3);
fromHeadtoTailPrintLinkedListByStack(head);
System.out.println();
fromHeadtoTailPrintLinkedListByRecursion(head);
}
}
7 重建二叉树

根据前序和中序遍历,可以确定每颗子树根节点所在的位置,然后根据根节点,划分左右子树,之后再分别在左右子树中重复之前的划分过程。(递归实现)
public static Node constructBinaryTreeByPreInOrder(int[] preOrder, int[] inOrder, int preOrder_start,
int inOrder_start, int length) {
if (length == 0) {
return null;
}
int rootInOrderIndex = 0;
for (int i = inOrder_start; i < inOrder_start + length; i++) {
if (preOrder[preOrder_start] == inOrder[i]) {
rootInOrderIndex = i;
break;
}
}
int left_length = rootInOrderIndex - inOrder_start;
int right_length = length - left_length - 1;
//根节点
Node root = new Node(preOrder[preOrder_start]);
//构建左子树
root.left = constructBinaryTreeByPreInOrder(preOrder, inOrder, preOrder_start + 1,
inOrder_start, left_length);
//构建右子树
root.right = constructBinaryTreeByPreInOrder(preOrder, inOrder, preOrder_start + left_length + 1,
rootInOrderIndex + 1, right_length);
return root;
}
8 二叉树的下一个节点

分三种情况:
- 当前节点有右子树,下一个节点是右子树中最左的节点
- 无右子树
- 父节点的左孩子是当前节点,下一个节点是父节点
- 遍历该节点的父节点,直到父节点的左孩子是当前节点,下一个节点是父节点
public class TreeNode {
public int value;
public TreeNode left;
public TreeNode right;
public TreeNode parent;
public TreeNode(int value) {
this.value = value;
}
}
public static TreeNode findNextNode(TreeNode treeNode) {
//当前节点有右子树,下一个节点是右子树中最左的节点
if (treeNode.right != null) {
TreeNode cur = treeNode.right;
while (cur.left != null) {
cur = cur.left;
}
return cur;
} else {
//无右子树
TreeNode par = treeNode.parent;
//父节点的左孩子是当前节点,下一个节点是父节点
if (par.left == treeNode) {
return par;
} else {
//遍历该节点的父节点,直到父节点的左孩子是当前节点,下一个节点是父节点
while (par.left != treeNode) {
par = par.parent;
treeNode = treeNode.parent;
}
return par;
}
}
}
9 用两个栈实现队列

delteHead和getHead操作:只有stackPop为空时,才能往里面压入数据
import java.util.Stack;
public class TwoStackToQueue<T> {
private Stack<T> stackPush;
private Stack<T> stackPop;
public TwoStackToQueue() {
stackPush = new Stack<T>();
stackPop = new Stack<T>();
}
public void appendTail(T node) {
stackPush.push(node);
}
public T deleteHead() {
if (stackPush.isEmpty() && stackPop.isEmpty()) {
throw new RuntimeException("Queue is empty!");
} else {
if (stackPop.isEmpty()) {
while (!stackPush.isEmpty()) {
stackPop.push((stackPush.pop()));
}
}
return stackPop.pop();
}
}
public T getHead(){
if (stackPush.isEmpty() && stackPop.isEmpty()) {
throw new RuntimeException("Queue is empty!");
} else {
if (stackPop.isEmpty()) {
while (!stackPush.isEmpty()) {
stackPop.push((stackPush.pop()));
}
}
return stackPop.peek();
}
}
public static void main(String[] args) {
TwoStackToQueue twoStackToQueue = new TwoStackToQueue();
twoStackToQueue.appendTail(1);
twoStackToQueue.appendTail(2);
twoStackToQueue.appendTail(3);
twoStackToQueue.appendTail(4);
System.out.println(twoStackToQueue.deleteHead());
System.out.println(twoStackToQueue.deleteHead());
System.out.println(twoStackToQueue.deleteHead());
twoStackToQueue.appendTail(5);
System.out.println(twoStackToQueue.deleteHead());
System.out.println(twoStackToQueue.getHead());
System.out.println(twoStackToQueue.deleteHead());
System.out.println(twoStackToQueue.deleteHead());
}
}
用两个队列实现栈
引入队列queue1和queue2,每次pop操作,就将queue1中的节点都放入queue2中,直至queue1中的节点个数为1,然后再将queue1的节点poll,之后,再交换queue1和queue2中的值。peek操作类似。
import java.util.LinkedList;
import java.util.Queue;
public class TwoQueueToStack<T> {
private Queue<T> queue1;
private Queue<T> queue2;
public TwoQueueToStack() {
queue1 = new LinkedList<T>();
queue2 = new LinkedList<T>();
}
public void push(T node) {
queue1.add(node);
}
public T pop() {
if (queue1.isEmpty() && queue2.isEmpty()) {
throw new RuntimeException("the stack is empty!");
}
while (queue1.size() != 1) {
queue2.add(queue1.poll());
}
T node = queue1.poll();
Queue<T> queue = queue1;
queue1 = queue2;
queue2 = queue;
return node;
}
public T peek() {
if (queue1.isEmpty() && queue2.isEmpty()) {
throw new RuntimeException("the stack is empty!");
}
T node = null;
while (!queue1.isEmpty()) {
node = queue1.poll();
queue2.add(node);
}
Queue<T> queue = queue1;
queue1 = queue2;
queue2 = queue;
return node;
}
public static void main(String[] args) {
TwoQueueToStack twoQueueToStack = new TwoQueueToStack();
twoQueueToStack.push(1);
twoQueueToStack.push(2);
twoQueueToStack.push(3);
System.out.println(twoQueueToStack.pop());
twoQueueToStack.push(4);
System.out.println(twoQueueToStack.peek());
System.out.println(twoQueueToStack.pop());
System.out.println(twoQueueToStack.pop());
System.out.println(twoQueueToStack.pop());
System.out.println(twoQueueToStack.pop());
}
}
10 斐波那契数列

1.递归,时间复杂度O(2n)
2.循环,时间复杂度O(n
public class Fibonacci_10 {
public static int calFibonacciRecursive(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
return calFibonacciRecursive(n - 1) + calFibonacciRecursive(n - 2);
}
public static int calFibonacciNoRecursive(int n) {
int[] res={0,1};
if(n<2){
return res[n];
}
int f1=0;
int f2=1;
int f=0;
for (int i = 2; i <=n; i++) {
f=f1+f2;
f1=f2;
f2=f;
}
return f;
}
public static void main(String[] args) {
System.out.println(calFibonacciRecursive(10));
System.out.println(calFibonacciNoRecursive(20));
}
}
应用


11 旋转数组的最小数字

解法:
- 暴力,时间复杂度O(n)
- 二分查找,时间复杂度O(logn)。使用两个指针p1,p2,然后根据计算的mid值来移动p1,p2。
- 当arr[p1]== arr[mid] == arr[p2]时,无法判断p1和p2属于哪个递增子数组,直接调用getMin,进行顺序查找。
- 当arr[mid]>=arr[p1]时,mid属于p1所在的递增子数组,令p1=mid,继续二分。
- 当arr[mid]<=arr[p2]时,处理过程和2类似。
三种输入情况:
- 1,2,3,4,5
- 3,4,5,1,2
- 1,1,1,0,1
import org.jetbrains.annotations.NotNull;
public class FindMinNumberInRotateArray_11 {
public static int findByDichotomy(int[] arr) {
if (arr[0] < arr[arr.length - 1]) {
return arr[0];
}
int p1 = 0;
int p2 = arr.length - 1;
int mid = 0;
int min = arr[0];
while (arr[p1] >= arr[p2]) {
if (p1 + 1 == p2) {
min = arr[p2];
break;
}
mid = p1 + ((p2 - p1) >> 1);
if (arr[mid] == arr[p1] && arr[mid] == arr[p2]) {
return getMin(arr, p1, p2);
}
if (arr[mid] >= arr[p1]) {
p1 = mid;
} else if (arr[mid] <= arr[p2]) {
p2 = mid;
}
}
return min;
}
private static int getMin(int[] arr, int p1, int p2) {
int min = arr[p1];
for (int i = p1 + 1; i < p2; i++) {
if (min > arr[i]) {
min = arr[i];
}
}
return min;
}
public static int findByForce(int[] arr) {
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (min > arr[i]) {
min = arr[i];
}
}
return min;
}
public static void main(String[] args) {
int[] arr = {3, 4, 5, 1, 2};
int[] arr1 = {1, 2, 3, 4, 5};
int[] arr2 = {1, 0, 1, 1, 1};
int[] arr3 = {1};
System.out.println(comparator(arr));
System.out.println(comparator(arr1));
System.out.println(comparator(arr2));
System.out.println(comparator(arr3));
}
@NotNull
public static String comparator(int[] arr) {
return findByDichotomy(arr) == findByForce(arr) ? "true" : "false";
}
}
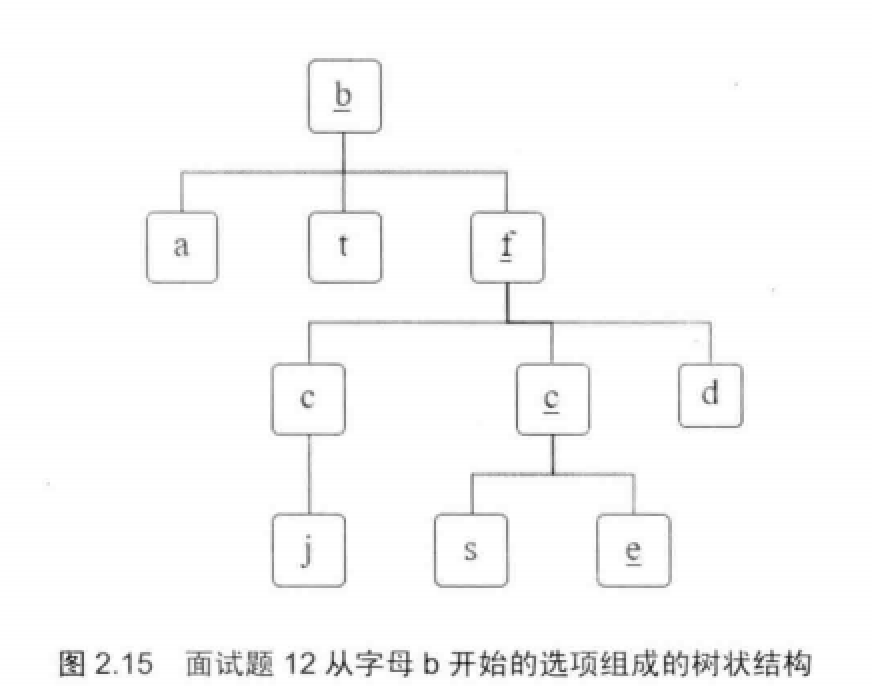
12 矩阵中的路径

思路:
回溯法,字符的遍历过程如下所示
public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
if (matrix == null || str == null || rows <= 0 || cols <= 0) {
return false;
}
//标记数组,用来记录该字符是否访问过
boolean[][] mark = new boolean[rows][cols];
char[][] chars = toArray(matrix, rows, cols);
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (process(chars, str, 0, mark, i, j)) {
return true;
}
}
}
return false;
}
//将一维数组转换成二维数组
public char[][] toArray(char[] matrix, int rows, int cols) {
char[][] chars = new char[rows][cols];
for (int i = 0, index = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
chars[i][j] = matrix[index++];
}
}
return chars;
}
//递归函数
public boolean process(char[][] chars, char[] str, int pathLength, boolean[][] mark, int row, int column) {
//遍历的路径长度和字符串长度相等,说明,之前的字符都已经成功匹配,返回true
if (pathLength == str.length) {
return true;
}
//数组下标越界、字符不匹配、字符已经访问过,都返回false
if (row < 0 || column < 0 || row >= chars.length || column >= chars[0].length
|| chars[row][column] != str[pathLength] || mark[row][column]) {
return false;
}
//字符已访问,标记为true
mark[row][column] = true;
//递归遍历该字符傍边的字符,匹配成功,则路径长度加1
if (process(chars, str, pathLength + 1, mark, row - 1, column) ||
process(chars, str, pathLength + 1, mark, row + 1, column) ||
process(chars, str, pathLength + 1, mark, row, column - 1) ||
process(chars, str, pathLength + 1, mark, row, column + 1)) {
return true;
}
//该字符旁边的字符都不匹配,则说明这条路不符合,还原,将字符的遍历标记设置为false
mark[row][column] = false;
return false;
}
13 机器人的运动范围

思路:图的深度优先遍历
public int movingCount(int threshold, int rows, int cols) {
//标记数组
boolean[][] mark = new boolean[rows][cols];
//存储每个位置的数位和
int[][] matrix = new int[rows][cols];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
matrix[i][j] = getValue(i) + getValue(j);
}
}
return process(threshold, matrix, mark, 0, 0, rows, cols);
}
private int process(int threshold, int[][] matrix, boolean[][] mark, int i, int j, int rows, int cols) {
int count = 0;
//递归终止条件
if (i < 0 || j < 0 || i >= rows || j >= cols || matrix[i][j] > threshold || mark[i][j]) {
return 0;
}
//将访问过的位置标记为true
mark[i][j] = true;
//访问当前位置,加1,然后继续遍历该位置傍边的位置,累加起来,最终的返回值就是所能到达的格子数
count = 1 + process(threshold, matrix, mark, i - 1, j, rows, cols) + process(threshold, matrix, mark, i + 1, j, rows, cols) +
process(threshold, matrix, mark, i, j - 1, rows, cols) + process(threshold, matrix, mark, i, j + 1, rows, cols);
return count;
}
//计算一个整数的数位之和
public int getValue(int num) {
int res = 0;
int tmp = 0;
while (num / 10 > 0) {
tmp = num / 10;
res += num - tmp * 10;
num = tmp;
}
res += num;
return res;
}
14 剪绳子

public class cutRope_14 {
// 思路:
// f(n)=max(f(i)*f(n-i)),0<i<n
// f(n)表示把绳子剪成若干段后各段乘积的最大值
//1.递归
public int cutRope(int target) {
if (target < 2) {
return 0;
}
if (target == 2) {
return 1;
}
if (target == 3) {
return 2;
}
int max = 0;
for (int i = 1; i <= (target - 1) / 2; i++) {
max = Math.max(max, process(i) * process(target - i));
}
return max;
}
public int process(int target) {
//递归终止条件
if (target < 4) {
return target;
}
int max = 0;
for (int i = 1; i <= (target - 1) / 2; i++) {
max = Math.max(max, process(i) * process(target - i));
}
return max;
}
//2.动态规划,时间复杂度O(n^2),由递归转化而来
public int cutRopeDP(int target) {
if (target < 2) {
return 0;
}
if (target == 2) {
return 1;
}
if (target == 3) {
return 2;
}
int[] dp = new int[target + 1];
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
for (int i = 4; i <= target; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = Math.max(dp[i], dp[j] * dp[i - j]);
}
}
return dp[target];
}
// 3.贪心,时间复杂度O(1)
// n>4时,划分出尽可能多的3,因为3(n-3)>=2(n-2)
// n=4时,2*2 > 3*1,所以当划分出1和3时,要转变成2和2
// n<4时,特殊情况,单独处理
public int cutRopeGreedy(int target) {
if (target < 2) {
return 0;
}
if (target == 2) {
return 1;
}
if (target == 3) {
return 2;
}
int timeOf3 = target / 3;
if (target - timeOf3 * 3 == 1) {
timeOf3--;
}
int timeOf2 = (target - timeOf3 * 3) / 2;
int res = (int) (Math.pow(3, timeOf3) * Math.pow(2, timeOf2));
return res;
}
//测试
public static void main(String[] args) {
cutRope_14 cutRope_14 = new cutRope_14();
System.out.println(cutRope_14.cutRope(14));
System.out.println(cutRope_14.cutRopeDP(14));
System.out.println(cutRope_14.cutRopeGreedy(14));
}
}
15 二进制中1的个数

public class BinaryNumber_15 {
public int NumberOf1(int n) {
//数字在计算机中以二进制形式存储,负数在计算机中以补码存储,int类型的数据占4个字节
//为了防止负数右移出现死循环的情况,可以把1每次左移一位,然后和n比较
int res = 0;
int flag = 1;
while (flag != 0) {
if ((n & flag) != 0) {
res++;
}
flag = flag << 1;
}
return res;
}
public int NumberOf1Improve(int n) {
//(n-1)&n 每次运算的结果将n中二进制表示最右边的1变为0
int res = 0;
while (n != 0) {
n=(n-1)&n;
res++;
}
return res;
}
public static void main(String[] args) {
BinaryNumber_15 binaryNumber_15 = new BinaryNumber_15();
int res = binaryNumber_15.NumberOf1(-8);
System.out.println(res);
}
}
16 数值的整数次方

base=0,exponent<0是非法输入,给用户提示输入错误
提高运算效率:
public class NumberExponent_16 {
public double Power(double base, int exponent) {
//非法输入
if (base == 0 && exponent < 0) {
throw new RuntimeException("input number error!");
}
double res = 1;
double tmp = exponent;
if (exponent < 0) {
exponent = -exponent;
}
//O(n)
for (int i = 1; i <= exponent; i++) {
res = res * base;
}
if (tmp < 0) {
res = 1 / res;
}
return res;
}
public double PowerImprove(double base, int exponent) {
//非法输入
if (base == 0 && exponent < 0) {
throw new RuntimeException("input number error!");
}
double res = 1;
double tmp = exponent;
if (exponent < 0) {
exponent = -exponent;
}
if (exponent % 2 == 0) {
//O(n/2)
for (int i = 1; i <= exponent / 2; i++) {
res = res * base;
}
res = res * res;
} else {
for (int i = 1; i <= (exponent - 1) / 2; i++) {
res = res * base;
}
res = res * res * base;
}
if (tmp < 0) {
res = 1 / res;
}
return res;
}
}
17 打印从1到最大的n位数

本质上是0-9的全排列顺序输出问题,用递归实现。
大数问题,一般使用字符串来表示数字。
public class PrintMaxNumber_17 {
//n没有限定范围,大数问题,需要用字符串来表示
public void print(int n) {
if (n <= 0) {
throw new RuntimeException("error input!");
}
char[] nums=new char[n];
for (int i = 0; i < 10; i++) {
//数字转字符,'0' + i 是 i 的ascii码
nums[0]=(char)('0'+i);
process(nums,0,n);
}
}
public void process(char[] nums,int index,int len){
if(index==len-1){
print(nums);
return;
}
for (int i = 0; i < 10; i++) {
nums[index+1]=(char)('0'+i);
process(nums,index+1,len);
}
}
private void print(char[] nums) {
//标记位,用来判断数字0之前是否有非零数字出现过
int flag=0;
String str="";
for (int i = 0; i < nums.length; i++) {
if(nums[i]!='0'){
flag=1;
str+=nums[i];
}
if(nums[i]=='0'&&flag==1){
str+=nums[i];
}
}
System.out.print(str+" ");
}
public static void main(String[] args) {
PrintMaxNumber_17 printMaxNumber_17=new PrintMaxNumber_17();
printMaxNumber_17.print(3);
}
}
18 删除链表中的节点

链表中删除节点的两种方法:
public class DeleteNode_18 {
static class Node {
int value;
Node next;
public Node(int value) {
this.value = value;
}
}
//O(1)
public static Node deleteNode(Node head, Node deleteNode) {
//要删除节点的下一个节点不为空时,用下一个节点的值替代当前节点,然后将当前节点指向下一个节点的节点,O(1)
if (deleteNode.next != null) {
deleteNode.value = deleteNode.next.value;
deleteNode.next = deleteNode.next.next;
} else {
//链表中只有一个节点
if (head == deleteNode) {
head = null;
} else {
//要删除节点的下一个节点为空,即链表中最后一个节点,O(n)
Node cur = head;
while (cur.next != deleteNode) {
cur = cur.next;
}
cur.next = null;
}
}
return head;
}
public static void printNode(Node head) {
while (head != null) {
System.out.print(head.value + " ");
head = head.next;
}
}
public static void main(String[] args) {
Node node1 = new Node(1);
Node node2 = new Node(2);
Node node3 = new Node(3);
node1.next = node2;
node2.next = node3;
Node head = deleteNode(node1, node3);
printNode(head);
}
}
19 正则表达式匹配

当模式中的第二个字符不是 “*” 时:
1、如果字符串第一个字符和模式中的第一个字符相匹配,那么字符串和模式都后移一个字符,然后匹配剩余的。
2、如果 字符串第一个字符和模式中的第一个字符不匹配,直接返回 false。
而当模式中的第二个字符是 “*” 时:
如果字符串第一个字符跟模式第一个字符不匹配,则模式后移 2 个字符,继续匹配。如果字符串第一个字符跟模式第一个字符匹配,可以有 3 种匹配方式:
1、模式后移 2 字符,相当于 x * 被忽略;
2、字符串后移 1 字符,模式后移 2 字符;
3、字符串后移 1 字符,模式不变,即继续匹配字符下一位,因为 * 可以匹配多位;
这里需要注意的是:Java 里,要时刻检验数组是否越界。
public class RegularExpressionMatch_19 {
public boolean match(char[] str, char[] pattern) {
if (str == null || pattern == null) {
return false;
}
int strIndex = 0;
int patternIndex = 0;
return matchCore(str, strIndex, pattern, patternIndex);
}
public boolean matchCore(char[] str, int strIndex, char[] pattern, int patternIndex) {
//有效性检验:str到尾,pattern到尾,匹配成功
if (strIndex == str.length && patternIndex == pattern.length) {
return true;
}
//pattern先到尾,匹配失败
if (strIndex != str.length && patternIndex == pattern.length) {
return false;
}
//模式第2个是*,且字符串第1个跟模式第1个匹配,分3种匹配模式;如不匹配,模式后移2位
if (patternIndex + 1 < pattern.length && pattern[patternIndex + 1] == '*') {
if ((strIndex != str.length && pattern[patternIndex] == str[strIndex])
|| strIndex != str.length && (pattern[patternIndex] == '.')) {
return matchCore(str, strIndex, pattern, patternIndex + 2)// 模式后移2,视为x*匹配0个字符
|| matchCore(str, strIndex + 1, pattern, patternIndex + 2)// 视为模式匹配1个字符
|| matchCore(str, strIndex + 1, pattern, patternIndex);// *匹配1个,再匹配str中的下一个
} else {
return matchCore(str, strIndex, pattern, patternIndex + 2);
}
}
//模式第2个不是*,且字符串第1个跟模式第1个匹配,则都后移1位,否则直接返回false
if ((strIndex != str.length && pattern[patternIndex] == str[strIndex])
|| (strIndex != str.length && pattern[patternIndex] == '.')) {
return matchCore(str, strIndex + 1, pattern, patternIndex + 1);
}
return false;
}
public static void main(String[] args) {
RegularExpressionMatch_19 regularExpressionMatch_19 = new RegularExpressionMatch_19();
boolean res = regularExpressionMatch_19.match("".toCharArray(), ".*".toCharArray());
System.out.println(res);
}
}
20 表示数值的字符串

使用正则表达式进行匹配
[] : 字符集合
() : 分组
? : 重复 0 ~ 1 次+ : 重复 1 ~ n 次
* : 重复 0 ~ n 次
. : 任意字符
\\. : 转义后的 .
\\d : 数字
import java.util.ArrayList;
import java.util.List;
public class JudgeNumber_20 {
public boolean judge(String str) {
if (str == null || str.length() == 0)
return false;
return str.matches("[+-]?\\d*(\\.\\d+)?([eE][+-]?\\d+)?");
}
public static void main(String[] args) {
JudgeNumber_20 judgeNumber_20 = new JudgeNumber_20();
String[] strings = {"+100", "5e2", "-123", "3.1416", "-1E-16",
"12e", "1a3.14", "1.2.3", "+-5", "12e+4.3" };
for (String str : strings) {
System.out.println(str + " " + judgeNumber_20.judge(str));
}
}
}
21 调整数组顺序使奇数位于偶数前面

使用双指针begin和end
begin=0,end=arr.length-1
public class OddEvenNumber_21 {
public void adjust(int[] arr) {
int begin = 0;
int end = arr.length - 1;
while (begin < end) {
while (judgeOddEven(arr[begin]) && begin < end) {
begin++;
}
while (!judgeOddEven(arr[begin]) && begin < end) {
end--;
}
swap(arr, begin, end);
}
}
public boolean judgeOddEven(int i) {
return i % 2 == 0;
}
public void swap(int[] arr, int begin, int end) {
int tmp = arr[begin];
arr[begin] = arr[end];
arr[end] = tmp;
}
public void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
OddEvenNumber_21 oddEvenNumber_21 = new OddEvenNumber_21();
int[] arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 20);
}
oddEvenNumber_21.printArray(arr);
oddEvenNumber_21.adjust(arr);
oddEvenNumber_21.printArray(arr);
}
}
22 链表中倒数第k个节点

设置两个指针p1、p2,p1=p2=head
让p1先走k-1步,然后p1和p2同时走,p1走到链表尾结点,则p2正好走到倒数第k个节点
代码鲁棒性:
- 输入的链表头指针为null
- k=0
- 链表中节点个数小于k
public class TheLastKthNode_22 {
static class ListNode {
int value;
ListNode next;
ListNode(int value) {
this.value = value;
}
}
public static ListNode theLastKthNode(ListNode head, int k) {
if(head==null){
throw new RuntimeException("Error,head is null!");
}
if(k==0){
throw new RuntimeException("Error,the value of k is 0!");
}
ListNode p1 = head;
ListNode p2 = head;
int i=0;
while (i != (k - 1)) {
if(p1.next==null){
throw new RuntimeException("Error,the number of ListNode is less than k!");
}
p1 = p1.next;
i++;
}
while (p1.next != null) {
p1 = p1.next;
p2 = p2.next;
}
return p2;
}
public static void main(String[] args) {
ListNode listNode1 = new ListNode(1);
ListNode listNode2 = new ListNode(2);
ListNode listNode3 = new ListNode(3);
ListNode listNode4 = new ListNode(4);
ListNode listNode5 = new ListNode(5);
ListNode listNode6 = new ListNode(6);
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
listNode4.next = listNode5;
listNode5.next = listNode6;
ListNode listNode=theLastKthNode(listNode1,8);
System.out.println(listNode.value);
}
}
23 链表中环的入口节点

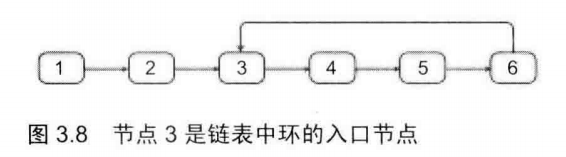
思路:
- 先判断链表是否存在环,使用快慢指针,快指针一次走两步,慢指针一次走一步,两个指针相遇,则说明链表有环,记录下相遇时候的节点LoopNode
- 计算环中的节点个数,从LoopNode节点出发,再次回到LoopNode,就得到了环中节点的个数k
- 设置两个指针p1和p2,让p1先走k步,然后p1和p2同时走,相遇时候的节点EntryNode即为环的入口节点
public class LoopOfLinkedList_23 {
static class LinkedList {
int value;
LinkedList next;
LinkedList(int value) {
this.value = value;
}
}
public static LinkedList findLoopNode(LinkedList head) {
if (head == null) {
throw new RuntimeException("head is null!");
}
LinkedList p1 = head.next;
LinkedList p2 = head;
LinkedList loopNode = null;
while (p1.next != null) {
p1 = p1.next;
if (p1.next != null) {
p1 = p1.next;
}
p2 = p2.next;
// System.out.println(p1.value + " " + p2.value);
if (p1 == p2) {
loopNode = p1;
break;
}
}
if (loopNode == null) {
return null;
}
int count = 1;
LinkedList tmpList=loopNode;
while (loopNode.next != tmpList) {
count++;
// System.out.println(count);
loopNode = loopNode.next;
}
p1 = p2 = head;
while (count-- > 0) {
p1 = p1.next;
}
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
public static void main(String[] args) {
LinkedList linkedList1 = new LinkedList(1);
LinkedList linkedList2 = new LinkedList(2);
LinkedList linkedList3 = new LinkedList(3);
LinkedList linkedList4 = new LinkedList(4);
LinkedList linkedList5 = new LinkedList(5);
LinkedList linkedList6 = new LinkedList(6);
linkedList1.next = linkedList2;
linkedList2.next = linkedList3;
linkedList3.next = linkedList4;
linkedList4.next = linkedList5;
linkedList5.next = linkedList6;
linkedList6.next = linkedList3;
LinkedList linkedList = findLoopNode(linkedList1);
System.out.println(linkedList.value);
}
}
24 反转链表

- 非递归:使用一个newList节点来记录逆向之后的头结点
- 递归:每次递归,head.next要设置为null
public class ReverseLinkedList {
static class LinkedList {
int value;
LinkedList next;
LinkedList(int value) {
this.value = value;
}
}
//非递归
public static LinkedList reverse(LinkedList head) {
LinkedList newList = new LinkedList(-1);
while (head != null) {
LinkedList next = head.next;
head.next = newList.next;
newList.next = head;
head = next;
}
return newList.next;
}
//递归
public static LinkedList reverseByRecursive(LinkedList head){
if(head==null||head.next==null){
return head;
}
LinkedList next=head.next;
head.next=null;
LinkedList newHead=reverseByRecursive(next);
next.next=head;
return newHead;
}
public static void main(String[] args) {
LinkedList linkedList1 = new LinkedList(1);
LinkedList linkedList2 = new LinkedList(2);
LinkedList linkedList3 = new LinkedList(3);
LinkedList linkedList4 = new LinkedList(4);
LinkedList linkedList5 = new LinkedList(5);
LinkedList linkedList6 = new LinkedList(6);
linkedList1.next = linkedList2;
linkedList2.next = linkedList3;
linkedList3.next = linkedList4;
linkedList4.next = linkedList5;
linkedList5.next = linkedList6;
LinkedList reverseHead = reverse(linkedList1);
while (reverseHead!=null){
System.out.println(reverseHead.value);
reverseHead=reverseHead.next;
}
}
}
25 合并两个排序的链表

public class MergeSortedLinkedList_25 {
public static LinkedList mergeSortedLinkedList(LinkedList head1, LinkedList head2) {
LinkedList head = new LinkedList(-1);
LinkedList cur = head;
while (head1 != null && head2 != null) {
if (head1.value <= head2.value) {
cur.next = head1;
head1 = head1.next;
} else {
cur.next = head2;
head2 = head2.next;
}
cur = cur.next;
}
if (head1 != null) {
cur.next = head1;
}
if (head2 != null) {
cur.next = head2;
}
return head.next;
}
public static LinkedList mergeSortedLinkedListByRecursive(LinkedList head1, LinkedList head2) {
if (head1 == null) {
return head2;
}
if (head2 == null) {
return head1;
}
if (head1.value <= head2.value) {
head1.next = mergeSortedLinkedListByRecursive(head1.next, head2);
return head1;
} else {
head2.next = mergeSortedLinkedListByRecursive(head1, head2.next);
return head2;
}
}
}
26 树的子结构

public class SubTree_26 {
static class BinaryTreeNode {
double value;
BinaryTreeNode left;
BinaryTreeNode right;
BinaryTreeNode(int value) {
this.value = value;
}
}
//遍历所有根节点值相同的子树
public static boolean hasSubTree(BinaryTreeNode binaryTreeNode1, BinaryTreeNode binaryTreeNode2) {
boolean result = false;
if (binaryTreeNode1 != null && binaryTreeNode2 != null) {
if (binaryTreeNode1.value == binaryTreeNode2.value) {
result = judge(binaryTreeNode1, binaryTreeNode2);
}
if (!result) {
result = hasSubTree(binaryTreeNode1.left, binaryTreeNode2);
}
if (!result) {
result = hasSubTree(binaryTreeNode1.right, binaryTreeNode2);
}
}
return result;
}
//判断根节点相同的子树是否完全一样
public static boolean judge(BinaryTreeNode binaryTreeNode1, BinaryTreeNode binaryTreeNode2) {
if (binaryTreeNode2 == null) {
return true;
}
if (binaryTreeNode1 == null) {
return false;
}
if (!Equals(binaryTreeNode1.value, binaryTreeNode2.value)) {
return false;
} else {
return judge(binaryTreeNode1.left, binaryTreeNode2.left) && judge(binaryTreeNode1.right, binaryTreeNode2.right);
}
}
//计算机表示小数(float、double)存在误差,不能直接用等号判断两个小数是否相等。如果两个小数的差的绝对值很小,
// 小于0.0000001,则认为相等
public static boolean Equals(double a, double b) {
if (Math.abs(a - b) < 0.0000001) {
return true;
} else {
return false;
}
}
}
27 二叉树的镜像

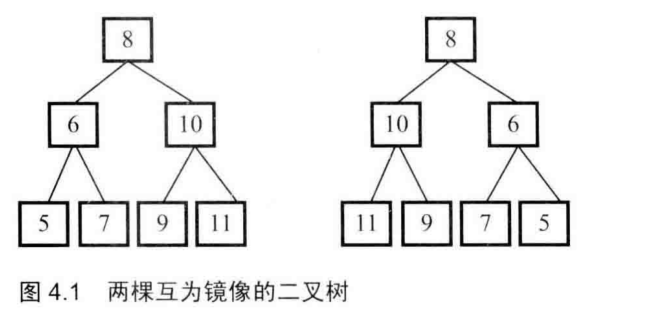
前序遍历,递归依次交换左右节点
public class BinaryTreeMirror_27 {
class BinaryTreeNode {
int value;
BinaryTreeNode left;
BinaryTreeNode right;
}
public void mirrorRecursive(BinaryTreeNode root) {
if (root == null) {
return;
}
if (root.left == null && root.right == null) {
return;
}
BinaryTreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
if (root.left != null) {
mirrorRecursive(root.left);
}
if (root.right != null) {
mirrorRecursive(root.right);
}
}
}
28 对称的二叉树

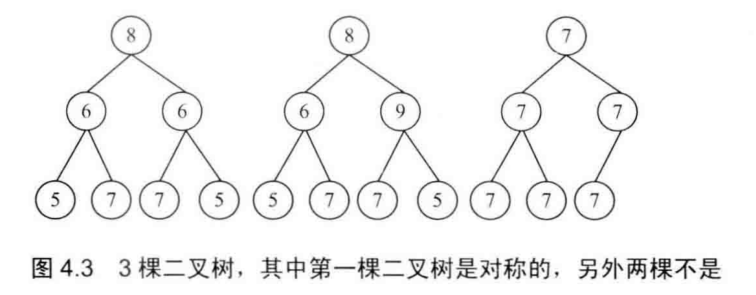
思路:比较二叉树的根左右和根右左遍历的序列,来进行判断
public class BinaryTreeSymmetry_28 {
class BinaryTreeNode {
int value;
BinaryTreeNode left;
BinaryTreeNode right;
}
public boolean isSymmetry(BinaryTreeNode root) {
return process(root, root);
}
public boolean process(BinaryTreeNode root1, BinaryTreeNode root2) {
if (root1 == null && root2 == null) {
return true;
}
if (root1 == null || root2 == null) {
return false;
}
if (root1.value != root2.value) {
return false;
}
return process(root1.left, root2.right) && process(root1.right, root2.left);
}
}
29 顺时针打印矩阵

每次打印一个圈,可以用递归或者循环实现
public class ClockwisePrintMatrix_29 {
public static void clockwisePrintMatrix(int[][] arr) {
if (arr == null) {
return;
}
print(arr, 0, 0, arr.length - 1, arr[0].length - 1);
}
public static void print(int[][] arr, int leftX, int leftY, int rightX, int rightY) {
//递归终止条件
if (leftX > rightX || leftY > rightY) {
return;
}
//单行和单列需要单独处理,否则会输出重复的序列
if (leftX == rightX) {
for (int i = leftY; i <= rightY; i++) {
System.out.print(arr[leftX][i] + " ");
}
} else if (leftY == rightY) {
for (int i = leftX; i <= rightX; i++) {
System.out.print(arr[i][leftY] + " ");
}
//其他情况,顺时针转圈打印,注意边界的处理
} else {
for (int i = leftY; i < rightY; i++) {
System.out.print(arr[leftX][i] + " ");
}
for (int i = leftX; i <= rightX; i++) {
System.out.print(arr[i][rightY] + " ");
}
for (int i = rightY - 1; i >= leftY; i--) {
System.out.print(arr[rightX][i] + " ");
}
for (int i = rightX - 1; i > leftX; i--) {
System.out.print(arr[i][leftY] + " ");
}
print(arr, ++leftX, ++leftY, --rightX, --rightY);
}
}
public static void main(String[] args) {
int[][] arr = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
int[][] arr1 = {
{1, 2, 3, 4},
};
int[][] arr2 = {
{1}, {2},{3}, {4},
};
clockwisePrintMatrix(arr);
System.out.println();
clockwisePrintMatrix(arr1);
System.out.println();
clockwisePrintMatrix(arr2);
/* result:
* 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
* 1 2 3 4
* 1 2 3 4
* */
}
}
30 包含min函数的栈

使用两个栈:dataStack和minStack。
dataStack存储实际的数据
minStack存储当前栈内元素最小的数据
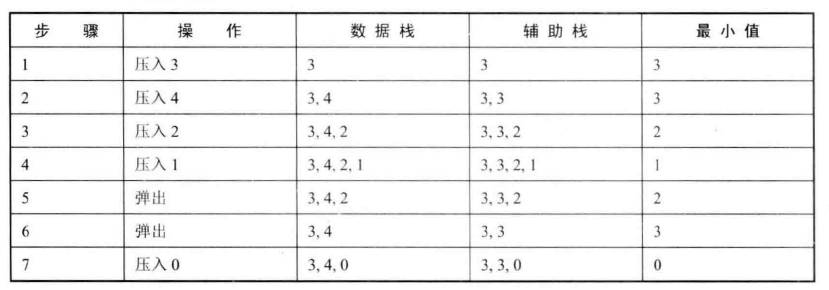
import java.util.Stack;
public class MinStack_30 {
Stack<Integer> dataStack;
Stack<Integer> minStack;
public MinStack_30() {
dataStack = new Stack<>();
minStack = new Stack<>();
}
public void push(int data) {
dataStack.push(data);
if (minStack.isEmpty()) {
minStack.push(data);
} else {
int min = minStack.peek();
if (data < min) {
min = data;
}
minStack.push(min);
}
}
public int pop() {
int data = dataStack.pop();
minStack.pop();
return data;
}
public int min() {
return minStack.peek();
}
public static void main(String[] args) {
MinStack_30 minStack = new MinStack_30();
minStack.push(3);
System.out.println(minStack.min());
minStack.push(4);
System.out.println(minStack.min());
minStack.push(2);
System.out.println(minStack.min());
minStack.push(1);
System.out.println(minStack.min());
minStack.pop();
System.out.println(minStack.min());
}
}
31 栈的压入、弹出序列
题目描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。
例如序列 1,2,3,4,5 是某栈的压入顺序,序列 4,5,3,2,1 是该压栈序列对应的一个弹出序列,但 4,3,5,1,2 就不可能是该压栈序列的弹出序列。
先往栈压入pushSequence的第一个数字pushSequence[0],然后将栈顶的数字和popSequence[index]的数字进行比较,相同就弹出栈顶元素,popIndex++;否则,pushIndex++,压入pushSequence[pushIndex]到栈。
import java.util.Stack;
public class SequenceStack_31 {
public static boolean judgeSequenceStack(int[] pushSequence, int[] popSequence) {
//使用stack模拟栈的压入弹出操作
Stack<Integer> stack = new Stack<>();
int n = pushSequence.length;
if (pushSequence == null || popSequence == null || n == 0) {
return false;
}
//pushIndex:压栈序列的下标;popIndex:出栈序列的下标
for (int pushIndex = 0, popIndex = 0; pushIndex < n; pushIndex++) {
stack.push(pushSequence[pushIndex]);
//栈顶元素和出栈序列下标的元素一样时,弹出栈顶元素,继续比较下一个出栈序列元素
while (!stack.isEmpty() && popIndex < n && stack.peek() == popSequence[popIndex]) {
stack.pop();
popIndex++;
}
}
return stack.isEmpty();
}
public static void main(String[] args) {
int[] pushSequence = {1, 2, 3, 4, 5};
int[] popSequence1 = {4, 5, 3, 2, 1};
int[] popSequence2 = {4, 3, 5, 1, 2};
System.out.println(judgeSequenceStack(pushSequence, popSequence1));
System.out.println(judgeSequenceStack(pushSequence, popSequence2));
}
}
32-1 从上到下打印二叉树
题目描述
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
例如,以下二叉树层次遍历的结果为:1,2,3,4,5,6,7
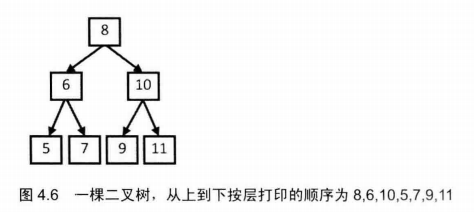
思路:使用队列(先进先出),先将根节点压入队列,然后开始遍历队列,每弹出一个节点就输出节点的值,然后将该节点的左右孩子压入队列,重复此过程直到队列为空。
import java.util.LinkedList;
import java.util.Queue;
public class PrintBinaryTree_32 {
public static class BinaryTree {
int value;
BinaryTree left;
BinaryTree right;
BinaryTree(int value) {
this.value = value;
}
}
public static void printBinaryTree(BinaryTree root) {
if (root == null) {
return;
}
Queue<BinaryTree> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
BinaryTree binaryTree = queue.poll();
if (binaryTree.left != null) {
queue.add(binaryTree.left);
}
if (binaryTree.right != null) {
queue.add(binaryTree.right);
}
if (!queue.isEmpty()) {
System.out.print(binaryTree.value + ",");
} else {
System.out.print(binaryTree.value);
}
}
}
public static void main(String[] args) {
BinaryTree root = new BinaryTree(8);
BinaryTree left1 = new BinaryTree(6);
BinaryTree right1 = new BinaryTree(10);
BinaryTree left21 = new BinaryTree(5);
BinaryTree right21 = new BinaryTree(7);
BinaryTree left22 = new BinaryTree(9);
BinaryTree right22 = new BinaryTree(11);
root.left = left1;
root.right = right1;
left1.left = left21;
left1.right = right21;
right1.left = left22;
right1.right = right22;
printBinaryTree(root);
}
}
32-2 分行从上到下打印二叉树
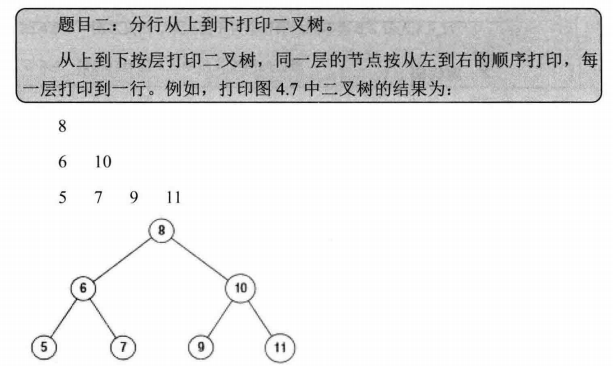
使用map来记录节点对应的层数,从0开始计数。
public static void printBinaryTree_2(BinaryTree root) {
if (root == null) {
return;
}
Queue<BinaryTree> queue = new LinkedList<>();
int index = 0;
Map<BinaryTree, Integer> map = new HashMap();
map.put(root, index);
queue.add(root);
int pre = index;
while (!queue.isEmpty()) {
BinaryTree binaryTree = queue.poll();
index = map.get(binaryTree);
index++;
if (binaryTree.left != null) {
map.put(binaryTree.left, index);
queue.add(binaryTree.left);
}
if (binaryTree.right != null) {
map.put(binaryTree.right, index);
queue.add(binaryTree.right);
}
if (pre != map.get(binaryTree)) {
System.out.println();
pre = map.get(binaryTree);
System.out.print(binaryTree.value);
} else {
if (map.get(binaryTree) == 0) {
System.out.print(binaryTree.value);
} else {
System.out.print(" " + binaryTree.value);
}
}
}
}
32-3 之字形打印二叉树
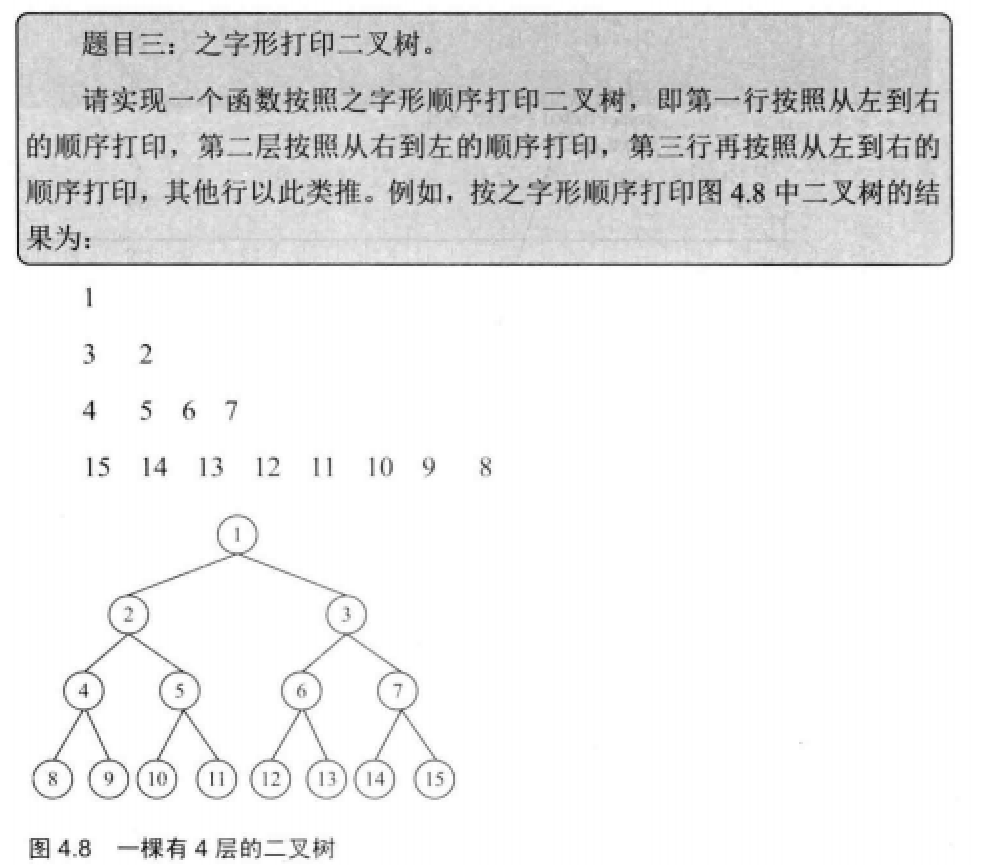
使用两个栈,一个栈存储当前层的节点,另一个栈存储下一次的节点。设置一个标志位flag,用于调整每一层节点的存储顺序。
public static void printBinaryTree_3(BinaryTree root) {
if (root == null) {
return;
}
Stack<BinaryTree> stack1 = new Stack<>();
Stack<BinaryTree> stack2 = new Stack<>();
//记录节点对应的层数
Map<BinaryTree, Integer> map = new LinkedHashMap<>();
int index = 0;
//根节点
map.put(root, index);
stack1.push(root);
int pre = index;
//标记变量
boolean flag = true;
/*每次处理一层,使用两个栈来存储节点*/
while (!stack1.isEmpty() || !stack2.isEmpty()) {
if (flag) {
while (!stack1.isEmpty()) {
BinaryTree node = stack1.pop();
index = map.get(node);
if (pre != index) {
System.out.println();
pre = index;
}
System.out.print(node.value + " ");
index++;
if (node.left != null) {
stack2.push(node.left);
map.put(node.left, index);
}
if (node.right != null) {
stack2.push(node.right);
map.put(node.right, index);
}
}
} else {
while (!stack2.isEmpty()) {
BinaryTree node = stack2.pop();
index = map.get(node);
if (pre != index) {
System.out.println();
pre = index;
}
System.out.print(node.value + " ");
index++;
if (node.right != null) {
stack1.push(node.right);
map.put(node.right, index);
}
if (node.left != null) {
stack1.push(node.left);
map.put(node.left, index);
}
}
}
flag = !flag;
}
}
33 二叉搜索树的后序遍历序列
题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。假设输入的数组的任意两个数字都互不相同。
例如,下图是后序遍历序列 1,3,2 所对应的二叉搜索树。
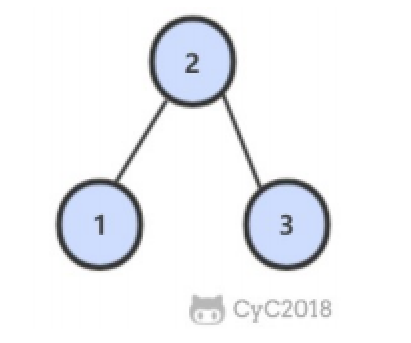
递归,后序遍历根节点在最后面,而二叉搜索树的特征是“左小右大”,以此为条件,来依次遍历左右子树。
import class_06.Edge;
public class PostOrderSequence_32 {
public static boolean judge(int[] arr) {
if (arr.length == 0) {
return false;
}
return process(arr, 0, arr.length - 1);
}
public static boolean process(int[] arr, int start, int end) {
if (end - start <= 0) {
return true;
}
// System.out.println(start);
// System.out.println(end);
int root = arr[end];
int cur = start;
while (cur < end && arr[cur] < root) {
cur++;
}
for (int i = cur; i < end; i++) {
if (arr[i] < root) {
return false;
}
}
return process(arr, start, cur - 1) && process(arr, cur, end - 1);
}
public static void main(String[] args) {
int[] arr1 = {5, 7, 6, 9, 11, 10, 8};
int[] arr2 = {7, 4, 6, 5};
int[] arr3 = {9, 11, 10, 8};
System.out.println(judge(arr1));
System.out.println(judge(arr2));
System.out.println(judge(arr3));
}
}
34 二叉树中和为某一值的路径

递归遍历
import java.util.ArrayList;
public class SumToPath_34 {
public static class BinaryTree {
int value;
BinaryTree left;
BinaryTree right;
BinaryTree(int value) {
this.value = value;
}
}
public static void sumToPath(BinaryTree binaryTree, int target) {
process(binaryTree, target, "");
}
public static void process(BinaryTree binaryTree, int target, String str) {
if (binaryTree == null) {
return;
}
str = str +binaryTree.value+"-";
target = target - binaryTree.value;
if (target == 0 && binaryTree.left == null && binaryTree.right == null) {
System.out.println(str);
}
process(binaryTree.left, target, str);
process(binaryTree.right, target, str);
}
/* private static ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();
private static ArrayList<Integer> list = new ArrayList<Integer>();
public static ArrayList<ArrayList<Integer>> FindPath(BinaryTree root, int target) {
if (root == null) return listAll;
list.add(root.value);
target -= root.value;
if (target == 0 && root.left == null && root.right == null)
listAll.add(new ArrayList<Integer>(list));
FindPath(root.left, target);
FindPath(root.right, target);
list.remove(list.size() - 1);
return listAll;
}*/
public static void main(String[] args) {
BinaryTree root = new BinaryTree(8);
BinaryTree left1 = new BinaryTree(6);
BinaryTree right1 = new BinaryTree(10);
BinaryTree left21 = new BinaryTree(5);
BinaryTree right21 = new BinaryTree(7);
BinaryTree left22 = new BinaryTree(9);
BinaryTree right22 = new BinaryTree(1);
root.left = left1;
root.right = right1;
left1.left = left21;
left1.right = right21;
right1.left = left22;
right1.right = right22;
sumToPath(root, 19);
/* ArrayList<ArrayList<Integer>> res = FindPath(root, 19);
for (int i = 0; i < res.size(); i++) {
System.out.println(res.get(i));
}*/
}
}
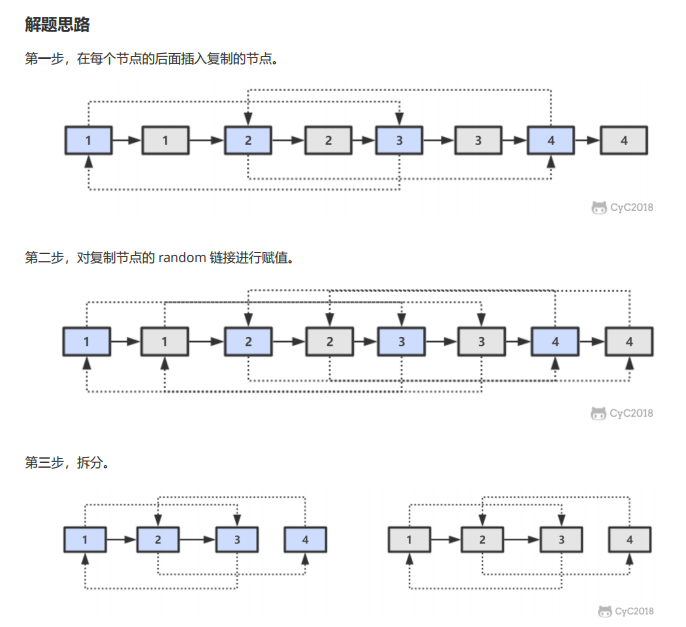
35 复杂链表的复制

public class CopyLinkedList_35 {
public static class ComplexListNode {
int value;
ComplexListNode next;
ComplexListNode random;
public ComplexListNode(int value) {
this.value = value;
}
}
public static ComplexListNode copy(ComplexListNode head) {
if (head == null) {
return null;
}
//第一步,复制节点
ComplexListNode cur = head;
while (cur != null) {
ComplexListNode copynode = new ComplexListNode(cur.value);
copynode.next = cur.next;
cur.next = copynode;
cur = copynode.next;
}
//第二步,建立random连接
cur = head;
while (cur != null) {
ComplexListNode copynode = cur.next;
if (cur.random != null) {
copynode.random = cur.random.next;
}
cur = copynode.next;
}
//第三步,拆分
cur = head;
ComplexListNode copyHead = head.next;
while (cur.next != null) {
ComplexListNode next = cur.next;
cur.next = next.next;
cur = next;
}
return copyHead;
}
}
36 二叉搜索树与双向链表
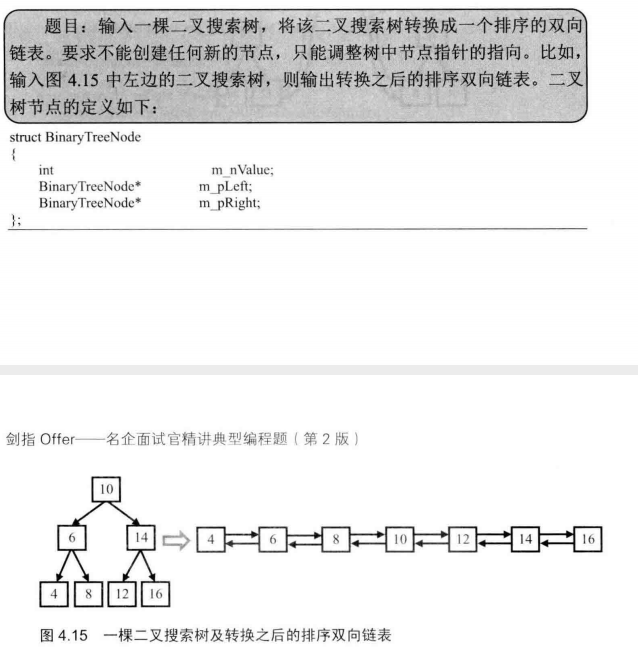
二叉搜索树的中序遍历是一个从小到大的有序序列,因此,只需在二叉树的中序递归遍历上做修改。
public class BinaryTreeLinkedList_36 {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
//pLast 用于记录当前链表的末尾节点。
private TreeNode pLast = null;
public TreeNode Convert(TreeNode root) {
if (root == null)
return null;
// 如果左子树为空,那么根节点root为双向链表的头节点
TreeNode head = Convert(root.left);
if (head == null)
head = root;
// 连接当前节点root和当前链表的尾节点pLast
root.left = pLast;
if (pLast != null)
pLast.right = root;
pLast = root;
Convert(root.right);
return head;
}
}
37 序列化二叉树

import java.util.LinkedList;
import java.util.Queue;
public class SerializationAndUnserializationBinaryTree_37 {
public static class BinaryTree {
int value;
BinaryTree left;
BinaryTree right;
BinaryTree(int value) {
this.value = value;
}
}
public static String serialization(BinaryTree root) {
if (root == null) {
return "$,";
}
String res = root.value + ",";
res += serialization(root.left);
res += serialization(root.right);
return res;
}
public static BinaryTree unSerialization(String str) {
String[] strings = str.split(",");
Queue<String> queue = new LinkedList();
for (int i = 0; i < strings.length; i++) {
queue.add(strings[i]);
}
return unSerializationByPreOrder(queue);
}
public static BinaryTree unSerializationByPreOrder(Queue<String> queue) {
String str = queue.poll();
if (str == "$") {
return null;
}
BinaryTree head = new BinaryTree(Integer.valueOf(str));
head.left = unSerializationByPreOrder(queue);
head.right = unSerializationByPreOrder(queue);
return head;
}
}
38 字符串的排列

思路:
- 求所有可能出现在第一个位置的字符
- 固定第一个字符,求后面所有字符的全排列,递归求解
public class PrintStringSequence_38 {
public static void printStringSequence(char[] chs, int index) {
if (index == chs.length - 1) {
System.out.print(String.valueOf(chs) + " ");
return;
}
for (int i = index; i < chs.length; i++) {
//确定第一个字符,求后面字符串的全排列
swap(chs, index, i);
printStringSequence(chs, index + 1);
//全排列完了,交换回来,保持原有顺序不变
swap(chs, index, i);
}
}
private static void swap(char[] chs, int index, int i) {
char c = chs[index];
chs[index] = chs[i];
chs[i] = c;
}
public static void main(String[] args) {
char[] chs="abc".toCharArray();
printStringSequence(chs,0);
/*
* result:abc acb bac bca cba cab
* */
}
}
扩展:
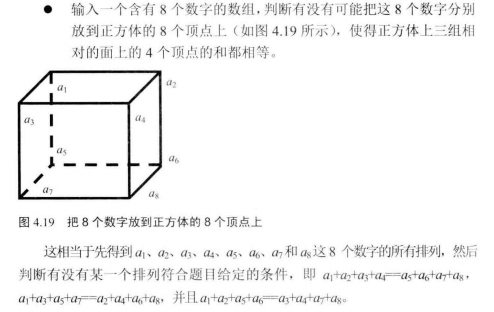


八皇后问题是一个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的 n 皇后摆放问题:这时棋盘的大小变为 n×n,而皇后个数也变成 n 。当且仅当n = 1 或 n ≥ 4 时问题有解 。
递归求解:
public class EightQueens_38_2 {
public static int count = 0;
public static void process(int[] ColumnIndex, int index) {
if (index == ColumnIndex.length - 1) {
for (int i = 0; i < ColumnIndex.length; i++) {
for (int j = 0; j < ColumnIndex.length; j++) {
//判断两个棋子是否在哎同一对角线上
if ((i != j) && (Math.abs(i - j) == Math.abs(ColumnIndex[i] - ColumnIndex[j]))) {
return;
}
}
}
count++;
return;
}
for (int i = index; i < ColumnIndex.length; i++) {
swap(ColumnIndex, index, i);
process(ColumnIndex, index + 1);
swap(ColumnIndex, index, i);
}
}
private static void swap(int[] ColumnIndex, int index, int i) {
int tmp = ColumnIndex[index];
ColumnIndex[index] = ColumnIndex[i];
ColumnIndex[i] = tmp;
}
public static void main(String[] args) {
int[] ColumnIndex = {0, 1, 2, 3, 4, 5, 6, 7};
process(ColumnIndex, 0);
System.out.println(count);
}
}
回溯法:
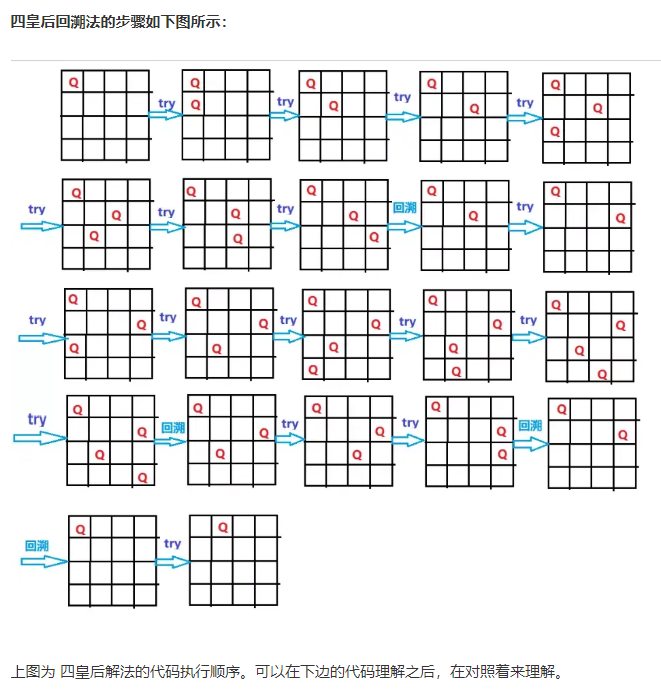
import java.util.Arrays;
public class QueenSolution {
//修改棋盘的大小,可模拟其他皇后类似问题
//模拟一个8X8的棋盘,0代表没有放置,1代表放置了一个皇后
private int[][] board = new int[8][8];
//解法的数量
private int total = 0;
/**
* 放置皇后的时候从第0行开始,依次放置一个
* 如果放置成功,那么继续放置下一行。(0-7)
* 当要放置k=8的时候说明已经全部放置完
* 毕了,找到了一个对应的解
*
* @param k 放置第几个皇后,K从0开始
*/
//放置第K个皇后
public void putQueen(int k) {
int max = board.length;
//放置第8个,说明棋盘已经放置完毕了,输出结果。
if (k >= max) {
//找到一个解,打印出来。
total++;
System.out.println(String.format("=============%s===============", total));
for (int i = 0; i < max; i++) {
System.out.println(Arrays.toString(board[i]));
}
System.out.println("=============================");
} else {
for (int i = 0; i < max; i++) {
if (check(k, i)) {
board[k][i] = 1;
putQueen(k + 1);
//回溯
board[k][i] = 0;
}
}
}
}
/**
* 皇后放置的时候是从上到下每一行放置的,所以不用检查改行以及之后的行
* 所以只用检查列以及左上右上对角线
*
* @param row 检查的对应行
* @param col 检查的对应列
* @return 返回改点是否满足可以放置一个皇后
*/
private boolean check(int row, int col) {
//检查列是否有皇后
for (int i = 0; i < row; i++) {
if (board[i][col] == 1) {
return false;
}
}
//检查左上对角线是否有皇后
for (int m = row - 1, n = col - 1; m >= 0 && n >= 0; m--, n--) {
if (board[m][n] == 1) {
return false;
}
}
//检查右上对角线是否有皇后
for (int m = row - 1, n = col + 1; m >= 0 && n < board[0].length; m--, n++) {
if (board[m][n] == 1) {
return false;
}
}
return true;
}
public static void main(String[] args) {
QueenSolution solution = new QueenSolution();
solution.putQueen(0);
}
}
39 数组中出现次数超过一半的数字

public class MoreThanHalfNumber_39 {
// 摩尔投票算法 , 能够在 O (n) 的时间和 O (1) 的空间解决问题
public static int getMoreThanHalfNumber(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int majority = nums[0];
int count = 0;
for (int i = 0; i < nums.length; i++) {
count = nums[i] == majority ? count + 1 : count - 1;
if (count == 0) {
majority = nums[i];
count = 1;
}
}
count = 0;
for (int i = 0; i < nums.length; i++) {
count = majority == nums[i] ? count + 1 : count;
}
return count > nums.length / 2 ? majority : -1;
}
}
扩展:找出所有出现次数大于 n/3 次的元素
最多只有两个,使用投票算法,将可能符合要求的两个元素找出来,然后再看它们是否都超过了 n/3, 来判断是否选择它们。
public static List<Integer> getMoreThan3_Number(int[] nums) {
if (nums == null || nums.length == 0) {
return new ArrayList<>();
}
int[] majority = new int[2];
int count1 = 0, count2 = 0;
//初始化要查找的两个不同的元素
majority[0] = nums[0];
majority[1] = -1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != majority[0]) {
majority[1] = nums[i];
break;
}
}
//摩尔投票算法
for (int i = 0; i < nums.length; i++) {
if (nums[i] == majority[0]) {
count1++;
} else if (nums[i] == majority[1]) {
count2++;
} else if (count1 == 0) {
majority[0] = nums[i];
count1 = 1;
} else if (count2 == 0) {
majority[1] = nums[i];
count2 = 1;
} else {
count1--;
count2--;
}
}
count1 = 0;
count2 = 0;
for (int i = 0; i < nums.length; i++) {
count1 = majority[0] == nums[i] ? count1 + 1 : count1;
count2 = majority[1] == nums[i] ? count2 + 1 : count2;
}
List<Integer> list = new ArrayList<>();
//最后再遍历一次数组,确认元素是否超过n/3次
if (count1 > nums.length / 3) {
list.add(majority[0]);
}
if (count2 > nums.length / 3) {
list.add(majority[1]);
}
return list;
}
40 最小的k个数

使用最大堆来存储数据,维持最大堆的节点个数为k个。
import java.util.ArrayList;
import java.util.Comparator;
import java.util.PriorityQueue;
public class KMinNumbers_40 {
public static ArrayList<Integer> getKMinNumbers(int[] nums, int k) {
if (k > nums.length || k <= 0) {
return new ArrayList<>();
}
//用最大堆来存储
PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
//最大堆中的结点个数超过k个,就移除堆顶结点
for (int i = 0; i < nums.length; i++) {
maxHeap.add(nums[i]);
if (maxHeap.size() > k) {
maxHeap.poll();
}
}
return new ArrayList<>(maxHeap);
}
}
41-1 数据流中的中位数

public static class Median {
private PriorityQueue<Integer> minHeap;
private PriorityQueue<Integer> maxHeap;
public Median() {
//小根堆
minHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
//大根堆
maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
}
public void add(int number) {
if (maxHeap.isEmpty()) {
maxHeap.add(number);
} else {
if (maxHeap.peek() >= number) {
maxHeap.add(number);
} else if (minHeap.isEmpty()) {
minHeap.add(number);
} else if (minHeap.peek() <= number) {
minHeap.add(number);
} else {
maxHeap.add(number);
}
}
modifyHeap();
}
//两个堆的节点个数之差大于2,就动态调整堆
public void modifyHeap() {
if (maxHeap.size() == minHeap.size() + 2) {
minHeap.add(maxHeap.poll());
}
if (minHeap.size() == maxHeap.size() + 2) {
maxHeap.add(minHeap.poll());
}
}
//取中位数,两个堆的节点个数加起来是偶数,中位数就是两个堆顶节点值相加除2;如果是奇数的话,中位数是节点个数多的堆的堆顶节点值。
public double getMeDian() {
int minHeapSize = minHeap.size();
int maxHeapSize = maxHeap.size();
double median = 0;
if ((minHeapSize + maxHeapSize) % 2 == 0) {
median = (minHeap.peek() + maxHeap.peek()) / 2.0;
} else {
median = minHeapSize > maxHeapSize ? minHeap.peek() : maxHeap.peek();
}
return median;
}
}
41-2 字符流中第一个不重复的字符
题目描述
请实现一个函数用来找出字符流中第一个只出现一次的字符。例如,当从字符流中只读出前两个字符 "go" 时,第一个只出现一次的字符是 "g"。当从该字符流中读出前六个字符“google" 时,第一个只出现一次的字符是 "l"。
使用队列来存储字符,因为队列先进先出的特性,所以,可以从第一个字符开始判断。然后使用一个int[256]的数组,来存储字符出现的个数。
import java.util.LinkedList;
import java.util.Queue;
public class FindFirstChar_41_2 {
private Queue<Character> queue = new LinkedList<>();
private int[] chars = new int[256];
//Insert one char from stringstream
public void Insert(char ch) {
chars[ch]++;
queue.add(ch);
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce() {
while (!queue.isEmpty()) {
if(chars[queue.peek()]==1){
return queue.peek();
}else {
queue.poll();
}
}
return '#';
}
}
42 连续子数组的最大和

思路:
动态规划
import java.lang.reflect.Array;
public class MaxSum_42 {
public int FindGreatestSumOfSubArray(int[] arr) {
int max = Integer.MIN_VALUE;
int sum = 0;
for (int i = 0; i < arr.length; i++) {
if (sum < 0) {
max = arr[i] > max ? arr[i] : max;
sum = arr[i];
} else {
sum += arr[i];
max = sum > max ? sum : max;
}
}
return max;
}
//动态规划
public int FindGreatestSumOfSubArray_2(int[] array) {
int[] s = array.clone();
int sum = 0;
for (int i = 0; i < array.length; i++) {
if (sum < 0) {
s[i] = array[i] > s[i] ? array[i] : s[i];
sum = array[i];
} else {
sum += array[i];
s[i] = sum > s[i] ? sum : s[i];
}
}
int max = s[0];
for (int i = 0; i < s.length; i++) {
max = s[i] > max ? s[i] : max;
}
return max;
}
public static void main(String[] args) {
MaxSum_42 maxSum_42 = new MaxSum_42();
int[] arr = {6, -3, -2, 7, -15, 1, 2, 2};
System.out.println(maxSum_42.FindGreatestSumOfSubArray(arr));
}
}
43 从 1 到 n 整数中 1 出现的次数

需要使用long类型的变量,使用int类型的变量在计算过程中会溢出。
public int countDigitOne(int n) {
long sum = 0;
long num = 1;
long preNumber = 0;
long curNumber = 0;
long sufNumber = 0;
while (num <= n) {
sufNumber = n % num;
curNumber = n % (num * 10) / num;
preNumber = n / (num * 10);
if (curNumber > 1) {
sum += num * (preNumber + 1);
} else if (curNumber == 1) {
sum += num * preNumber + sufNumber + 1;
} else {
sum += num * preNumber;
}
num = num * 10;
}
int res=(int)sum;
return res;
}
}
44 数字序列中某一位数字

public class NumSequence_44 {
public int getDigitAtIndex(int index) {
if (index < 0) {
return -1;
}
int digit = 1;
while (true) {
if (index < getDigitSum(digit)) {
return digitAtIndex(index, digit);
} else {
index -= getDigitSum(digit);
digit++;
}
}
}
//计算index的下标
private int digitAtIndex(int index, int digit) {
int begin = getBeginNumber(digit);
int shiftNumber = index / digit;
String number = (begin + shiftNumber) + "";
int count = index % digit;
return number.charAt(count) - '0';
}
//得到digit位开始的数字
private int getBeginNumber(int digit) {
if (digit == 1) {
return 0;
}
return (int) Math.pow(10, digit - 1);
}
//得到digit位的数字位数的总和
public int getDigitSum(int digit) {
if (digit == 1) {
return 10;
} else {
return digit * 9 * (int) (Math.pow(10, digit - 1));
}
}
public static void main(String[] args) {
NumSequence_44 numSequence_44 = new NumSequence_44();
System.out.println(numSequence_44.getDigitAtIndex(999));
}
}
45 把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组 {3,32,321},则打印出这三个数字能排成的最小数字为 321323。
可以看成是一个排序问题,在比较两个字符串 S1 和 S2 的大小时,应该比较的是 S1+S2 和 S2+S1 的大小,如果S1+S2 < S2+S1,那么应该把 S1 排在前面,否则应该把 S2 排在前面。
import java.util.Arrays;
import java.util.Comparator;
public class MinNumber_45 {
public String PrintMinNumber(int[] numbers) {
if (numbers == null || numbers.length == 0) {
return "";
}
String[] strings = new String[numbers.length];
for (int i = 0; i < numbers.length; i++) {
strings[i] = numbers[i] + "";
}
Arrays.sort(strings, new Comparator<String>() {
@Override
public int compare(String o1, String o2) {
return (o1 + o2).compareTo(o2 + o1);
}
});
/*lambda表达式
Arrays.sort(strings, (a, b) -> (a + b).compareTo(b + a));*/
String res = "";
for (int i = 0; i < strings.length; i++) {
res += strings[i];
}
return res;
}
}
46 把数字翻译成字符串
题目描述:
给定一个数字,按照如下规则翻译成字符串:1 翻译成“a”,2 翻译成“b”... 26 翻译成“z”。一个数字有多种翻译可能,例如 12258 一共有 5 种,分别是abbeh,lbeh,aveh,abyh,lyh。实现一个函数,用来计算一个数字有多少种不同的翻译方法。
public class NumberToString_46 {
public int numDecodings(String s) {
if (s == null || s.length() == 0) {
return 0;
}
return digui(s, 0);
}
private int digui(String s, int start) {
if (s.length() == start) {
return 1;
}
if (s.charAt(start) == '0') {
return 0;
}
//递归的递推式应该是如果index的后两位小于等于26,
// digui(s, start) = digui(s, start+1)+digui(s, start+2)
// 否则digui(s, start) = digui(s, start+1)
int ans1 = digui(s, start + 1);
int ans2 = 0;
if (start < s.length() - 1) {
int ten = (s.charAt(start) - '0') * 10;
int one = s.charAt(start + 1) - '0';
if (ten + one <= 26) {
ans2 = digui(s, start + 2);
}
}
return ans1 + ans2;
}
//动态规划
public int numDecodingsByDP(String s) {
if (s == null || s.length() == 0) {
return 0;
}
int len = s.length();
int[] dp = new int[len + 1];
dp[len] = 1;
if (s.charAt(len-1) == '0') {
dp[len - 1] = 0;
} else {
dp[len - 1] = 1;
}
for (int i = len - 2; i >= 0; i--) {
if (s.charAt(i) == '0') {
dp[i] = 0;
continue;
}
if (((s.charAt(i) - '0') * 10 + (s.charAt(i+1)-'0')) <= 26) {
dp[i] = dp[i + 1] + dp[i + 2];
} else {
dp[i] = dp[i + 1];
}
}
return dp[0];
}
public static void main(String[] args) {
String s = "12258";
System.out.println(new NumberToString_46().numDecodingsByDP(s));
//res:5
}
}
47 礼物的最大价值

public class MaxGiftValue_47 {
//递归
public int getMost(int[][] board) {
if (board == null || board.length == 0 || board[0].length == 0) {
return 0;
}
return process(board, 0, 0);
}
public int process(int[][] board, int i, int j) {
int res = board[i][j];
if (i == board.length - 1 && j == board[0].length - 1) {
return res;
}
if (i == board.length - 1) {
return res + process(board, i, j + 1);
}
if (j == board[0].length - 1) {
return res + process(board, i + 1, j);
}
return res + Math.max(process(board, i + 1, j), process(board, i, j + 1));
}
//动态规划(DP)
public int getMostByDP(int[][] board) {
if (board == null || board.length == 0 || board[0].length == 0) {
return 0;
}
int rows = board.length;
int columns = board[0].length;
int[][] dp = new int[rows][columns];
dp[0][0] = board[0][0];
for (int i = 1; i < rows; i++) {
dp[i][0] = dp[i - 1][0] + board[i][0];
}
for (int j = 1; j < columns; j++) {
dp[0][j] = dp[0][j - 1] + board[0][j];
}
for (int i = 1; i < rows; i++) {
for (int j = 1; j < columns; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + board[i][j];
}
}
return dp[rows - 1][columns - 1];
}
}
48 最长不含重复字符的子字符串
题目描述:
输入一个字符串(只包含 a~z 的字符),求其最长不含重复字符的子字符串的长度。例如对于 arabcacfr,最长不含重复字符的子字符串为 acfr,长度为 4。
思路:
动态规划,f(i)表示以第i个字符为结尾的不包含重复字符的子字符串的最长长度。如果第i个字符之前没有出现过,那么f(i)=f(i-1)+1;如果第i个字符出现过,先计算两个同样字符之间的距离d,如果d>f(i-1),说明第i个字符没有在f(i-1)的最长子字符串中出现过,f(i)=f(i-1)+1;如果d<=f(i-1),则说明第i个字符在f(i-1)的最长子字符串中出现过,f(i)=d.
public class MaxLengthSubString_48 {
public int maxLengthSubString(String s) {
if (s == null || s.length() == 0) {
return 0;
}
//int [26] 用于字母 ‘a’ - ‘z’ 或 ‘A’ - ‘Z’
//int [128] 用于 ASCII 码
//int [256] 用于扩展 ASCII 码
//ASCII码128位,初始化长度为128的数组,赋值为-1,表示当前字符没有出现
int[] pre = new int[128];
for (int i = 0; i < pre.length; i++) {
pre[i] = -1;
}
int maxLen = 0;
int curLen = 0;
for (int i = 0; i < s.length(); i++) {
int c = s.charAt(i);
int preIndex = pre[c];
if (preIndex == -1 || i - preIndex > curLen) {
curLen++;
maxLen = Math.max(curLen, maxLen);
} else {
maxLen = Math.max(curLen, maxLen);
int d = i - preIndex;
curLen = d;
}
pre[c] = i;
}
return maxLen;
}
public static void main(String[] args) {
System.out.println(new MaxLengthSubString_48().maxLengthSubString("arabcacfr"));
}
}
49 丑数
题目描述
把只包含因子 2、3 和 5 的数称作丑数(Ugly Number)。例如 6、8 都是丑数,但 14 不是,因为它包含因子 7。习惯上我们把 1 当做是第一个丑数。求按从小到大的顺序的第 N 个丑数。
链接:https://www.nowcoder.com/questionTerminal/6aa9e04fc3794f68acf8778237ba065b?f=discussion
来源:牛客网通俗易懂的解释:
首先从丑数的定义我们知道,一个丑数的因子只有 2,3,5,那么丑数 p = 2 ^ x * 3 ^ y * 5 ^ z,换句话说一个丑数一定由另一个丑数乘以 2 或者乘以 3 或者乘以 5 得到,那么我们从 1 开始乘以 2,3,5,就得到 2,3,5 三个丑数,在从这三个丑数出发乘以 2,3,5 就得到 4,6,10,6,9,15,10,15,25 九个丑数,我们发现这种方 *** 得到重复的丑数,而且我们题目要求第 N 个丑数,这样的方法得到的丑数也是无序的。那么我们可以维护三个队列:
(1)丑数数组: 1
乘以 2 的队列:2
乘以 3 的队列:3
乘以 5 的队列:5
选择三个队列头最小的数 2 加入丑数数组,同时将该最小的数乘以 2,3,5 放入三个队列;
(2)丑数数组:1,2
乘以 2 的队列:4
乘以 3 的队列:3,6
乘以 5 的队列:5,10
选择三个队列头最小的数 3 加入丑数数组,同时将该最小的数乘以 2,3,5 放入三个队列;
(3)丑数数组:1,2,3
乘以 2 的队列:4,6
乘以 3 的队列:6,9
乘以 5 的队列:5,10,15
选择三个队列头里最小的数 4 加入丑数数组,同时将该最小的数乘以 2,3,5 放入三个队列;
(4)丑数数组:1,2,3,4
乘以 2 的队列:6,8
乘以 3 的队列:6,9,12
乘以 5 的队列:5,10,15,20
选择三个队列头里最小的数 5 加入丑数数组,同时将该最小的数乘以 2,3,5 放入三个队列;
(5)丑数数组:1,2,3,4,5
乘以 2 的队列:6,8,10,
乘以 3 的队列:6,9,12,15
乘以 5 的队列:10,15,20,25
选择三个队列头里最小的数 6 加入丑数数组,但我们发现,有两个队列头都为 6,所以我们弹出两个队列头,同时将 12,18,30 放入三个队列;
……………………
疑问:
1. 为什么分三个队列?
丑数数组里的数一定是有序的,因为我们是从丑数数组里的数乘以 2,3,5 选出的最小数,一定比以前未乘以 2,3,5 大,同时对于三个队列内部,按先后顺序乘以 2,3,5 分别放入,所以同一个队列内部也是有序的;
2. 为什么比较三个队列头部最小的数放入丑数数组?
因为三个队列是有序的,所以取出三个头中最小的,等同于找到了三个队列所有数中最小的。
实现思路:
我们没有必要维护三个队列,只需要记录三个指针显示到达哪一步;“|” 表示指针,arr 表示丑数数组;
(1)1
|2
|3
|5
目前指针指向 0,0,0,队列头 arr [0] * 2 = 2, arr [0] * 3 = 3, arr [0] * 5 = 5
(2)1 2
2 |4
|3 6
|5 10
目前指针指向 1,0,0,队列头 arr [1] * 2 = 4, arr [0] * 3 = 3, arr [0] * 5 = 5
(3)1 2 3
2| 4 6
3 |6 9
|5 10 15
目前指针指向 1,1,0,队列头 arr [1] * 2 = 4, arr [1] * 3 = 6, arr [0] * 5 = 5
………………
public class UglyNumber_49 {
public int getUglyNumber(int index) {
if(index==0){
return 0;
}
int res = 0;
int count = 0;
int i = 1;
while (true) {
if (judge(i)) {
count++;
if (count == index) {
res = i;
break;
}
}
i++;
}
return res;
}
private Boolean judge(int num) {
while (num % 2 == 0) {
num = num / 2;
}
while (num % 3 == 0) {
num = num / 3;
}
while (num % 5 == 0) {
num = num / 5;
}
if (num == 1) {
return true;
}
return false;
}
public int getUglyNumberByDP(int index) {
if(index==0){
return 0;
}
int i2 = 0, i3 = 0, i5 = 0;
int[] dp = new int[index];
dp[0] = 1;
for (int i = 1; i < index; i++) {
int next2 = dp[i2] * 2, next3 = dp[i3] * 3, next5 = dp[i5] * 5;
dp[i] = Math.min(next2, Math.min(next3, next5));
if (dp[i] == next2) {
i2++;
}
if (dp[i] == next3)
i3++;
if (dp[i] == next5)
i5++;
}
return dp[index - 1];
}
public static void main(String[] args) {
int num = new UglyNumber_49().getUglyNumber(1500);
System.out.println(num);
int num_1 = new UglyNumber_49().getUglyNumberByDP(1500);
System.out.println(num_1);
}
}
50-1 第一个只出现一次的字符位置
题目描述
在一个字符串中找到第一个只出现一次的字符,并返回它的位置。
Input: abacc
Output: b
使用数组cnts来记录字符出现的次数,遍历两遍,时间复杂度O(n)
public class FirstNotRepeatingChar_50 {
public int FirstNotRepeatingChar(String str) {
//cnts,下标表示字符的ascii码,值表示字符出现的次数。
int[] cnts = new int[256];
for (int i = 0; i < str.length(); i++) {
cnts[str.charAt(i)]++;
}
for (int i = 0; i < str.length(); i++) {
if (cnts[str.charAt(i)] == 1) {
return i;
}
}
return -1;
}
public static void main(String[] args) {
System.out.println(new FirstNotRepeatingChar_50().FirstNotRepeatingChar("google"));
System.out.println(new FirstNotRepeatingChar_50().FirstNotRepeatingChar("NXWtnzyoHoBhUJaPauJaAitLWNMlkKwDYbbigdMMaYfkVPhGZcrEwp"));
char c=0;
System.out.println(c);
}
}
50-2 字符流中第一个只出现一次的字符

public class CharStatistics_50_2 {
//occurrence,下标表示字符的ascii码,值表示字符出现的位置。
public int[] occurrence = new int[256];
//插入的字符个数
public int index;
//构造函数
public CharStatistics_50_2() {
index = 0;
for (int i = 0; i < occurrence.length; i++) {
occurrence[i] = -1;
}
}
//插入
public void insert(char ch) {
if (occurrence[ch] == -1) {
occurrence[ch] = index;
} else {
occurrence[ch] = -2;
}
index++;
}
//得到第一个只出现一次的字符
public char firstAppearingOnce() {
char ch = 0;
int minIndex = Integer.MAX_VALUE;
for (int i = 0; i < 256; i++) {
if (occurrence[i] >= 0 && occurrence[i] < minIndex) {
ch = (char) i;
minIndex = occurrence[i];
}
}
return ch;
}
}
51 数组中的逆序对
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
public class InversePairs_51 {
// O(n^2)
public int InversePairs(int[] array) {
if (array == null || array.length < 2) {
return 0;
}
long res = 0;
for (int i = 0; i < array.length - 1; i++) {
for (int j = i + 1; j < array.length; j++) {
if (array[i] > array[j]) {
res++;
}
}
}
return (int) (res % 1000000007);
}
//辅助数组
private int[] help;
// O(nlogn)
public int InversePairsByMergeSort(int[] array) {
if (array == null || array.length < 2) {
return 0;
}
return (int) (mergeSort(array, 0, array.length - 1) % 1000000007);
}
// 归并排序
private long mergeSort(int[] array, int left, int right) {
if (left == right) {
return 0;
}
int mid = left + ((right - left) >> 1);
return mergeSort(array, left, mid) + mergeSort(array, mid + 1, right) + merge(array, left, mid, right);
}
private long merge(int[] array, int left, int mid, int right) {
help = new int[right - left + 1];
int i = 0;
int p1 = left;
int p2 = mid + 1;
long res = 0;
// 关键代码
// 每次合并的时候,统计逆序对的个数,合并完成之后,局部有序。使用归并排序,可以减少重复的比较次数,从而缩短时间复杂度。
while (p1 <= mid && p2 <= right) {
if (array[p1] > array[p2]) {
for (int j = p2; j <= right; j++) {
res++;
}
}
help[i++] = array[p1] > array[p2] ? array[p1++] : array[p2++];
}
while (p1 <= mid) {
help[i++] = array[p1++];
}
while (p2 <= right) {
help[i++] = array[p2++];
}
for (int j = 0; j < help.length; j++) {
array[left + j] = help[j];
}
return res;
}
public static void main(String[] args) {
int[] arr = {7, 5, 6, 4};
// System.out.println(new InversePairs_51().InversePairs(arr));
System.out.println(new InversePairs_51().InversePairsByMergeSort(arr));
}
}
52 两个链表的第一个公共结点
import java.util.HashSet;
public class FindFirstCommonNode_52 {
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
// 使用HashSet
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
HashSet<ListNode> hashSet = new HashSet<>();
ListNode head1 = pHead1;
ListNode head2 = pHead2;
while (head1 != null) {
hashSet.add(head1);
head1 = head1.next;
}
while (head2 != null) {
if (hashSet.contains(head2)) {
return head2;
}
head2 = head2.next;
}
return null;
}
// 先遍历两个链表,获得链表的长度,让较长的链表头指针先移动,使得两个链表剩余的节点个数相同,之后,两个链表的头指针同时开始移动,
// 出现第一个相同值的节点,即为第一个公共节点。
public ListNode FindFirstCommonNode_2(ListNode pHead1, ListNode pHead2) {
int len1 = 0, len2 = 0;
ListNode head1 = pHead1;
ListNode head2 = pHead2;
while (head1 != null) {
len1++;
head1 = head1.next;
}
while (head2 != null) {
len2++;
head2 = head2.next;
}
int max = Math.max(len1, len2);
int move1 = max - len1;
int move2 = max - len2;
head1 = pHead1;
head2 = pHead2;
//下面两个循环只会执行一个
while (move2 != 0) {
head1 = head1.next;
move2--;
}
while (move1 != 0) {
head2 = head2.next;
move1--;
}
while (head1 != null && head2 != null) {
if (head1.val == head2.val) {
return head1;
}
head1 = head1.next;
head2 = head2.next;
}
return null;
}
}
沟通能力和学习能力、知识迁移能力
53-1 数字在排序数组中出现的次数
题目描述
Input:
nums = 1, 2, 3, 3, 3, 3, 4, 6
K = 3
Output:
4
public class GetNumberOfK_53 {
public int getNumberOfK(int[] array, int k) {
// 二分查找,时间复杂度O(logn),logn是while循环的次数。
int first = getFirst(array, k);
int last = getLast(array, k);
// System.out.println(first + " " + last);
return last - first + 1;
}
//获取k第一次出现的下标
int getFirst(int[] data, int k) {
int start = 0, end = data.length - 1;
int mid = (start + end) / 2;
while (start <= end) {
if (data[mid] < k) {
start = mid + 1;
} else {
end = mid - 1;
}
mid = (start + end) / 2;
}
// start指向第一个小于k的数的下标,while循环结束,返回的start表示k第一次出现的下标。
// 如果k不存在,则返回第一个大于k的数的下标。
return start;
}
//获取k最后一次出现的下标
int getLast(int[] data, int k) {
int start = 0, end = data.length - 1;
int mid = (start + end) / 2;
while (start <= end) {
if (data[mid] <= k) {
start = mid + 1;
} else {
end = mid - 1;
}
mid = (start + end) / 2;
}
// end指向第一个大于k的数的下标,while循环结束,返回的end表示k最后一次出现的下标。
// 如果k不存在,则返回第一个小于k的数的下标。
return end;
}
public static void main(String[] args) {
int[] arr1 = {1, 2, 3, 3, 3, 3, 4, 6};
int[] arr2 = {3, 3, 3, 3, 4, 5};
int[] arr3 = {1, 2, 3, 4, 6};
System.out.println(new GetNumberOfK_53().getNumberOfK(arr1, 3));
System.out.println(new GetNumberOfK_53().getNumberOfK(arr2, 3));
System.out.println(new GetNumberOfK_53().getNumberOfK(arr3, 5));
}
}
53-2 0~n-1中缺失的数字

public class MissingNumber_53_2 {
//有序数组,使用二分查找
public int getMissingNumber(int[] arr, int len) {
//边界处理
if (arr == null || len <= 0) {
return -1;
}
int left = 0;
int right = len - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (arr[mid] != mid) {
if (mid == 0 || arr[mid - 1] == mid - 1) {
return mid;
}
right = mid - 1;
} else {
left = mid + 1;
}
}
if (left == len) {
return left;
}
return -1;
}
}
53-3 数组中数值和下标相等的元素

public class NumberEqualIndex_53_3 {
public int getNumberEqualIndex(int[] arr) {
if (arr == null || arr.length == 0) {
return -1;
}
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (arr[mid] == mid) {
return mid;
} else if (arr[mid] > mid) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
}
54 二叉查找树的第 K 个结点

二叉搜索树的中序遍历是一个递增序列
public class TheKthNode_54 {
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
private int cnt = 0;
private TreeNode res = null;
TreeNode KthNode(TreeNode pRoot, int k) {
InOrder(pRoot, k);
return res;
}
public void InOrder(TreeNode pRoot, int k) {
if (pRoot == null || cnt > k) {
return;
}
InOrder(pRoot.left, k);
cnt++;
if (cnt == k) {
res = pRoot;
}
InOrder(pRoot.right, k);
}
}
55-1 二叉树的深度
递归遍历,根节点的深度是左子树和右子树中较大的深度+1.
public class BinaryDepth_55 {
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public int TreeDepth(TreeNode root) {
if (root == null) {
return 0;
}
return 1 + Math.max(TreeDepth(root.left), TreeDepth(root.right));
}
}
55-2 平衡二叉树
题目描述:
public class IsBalanced_55_2 {
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public boolean IsBalanced_Solution(TreeNode root) {
return getHeight(root) != -1;
}
/*
* -1:表示非平衡二叉树
* 平衡二叉树左右子树高度之差不超过1,
* 因此,可以递归遍历左右子树的高度,只要左右子树高度之差大于1,就立即返回-1
* */
private int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int left = getHeight(root.left);
if (left == -1) {
return -1;
}
int right = getHeight(root.right);
if (right == -1) {
return -1;
}
return Math.abs(left - right) > 1 ? -1 : Math.max(left, right) + 1;
}
}
56-1 数组中只出现一次的两个数字
一个整型数组里除了两个数字只出现一次之外,其他的数字都出现了两次,找出这两个只出现一次的数字。
public class AppearOnceInArray_56 {
public void FindNumsAppearOnce(int[] array, int num1[], int num2[]) {
/*
位运算中异或的性质:两个相同数字异或为0,一个数和 0 异或还是它本身。
因此,array数组中数字异或的结果二进制中的1,表示的是两个只出现一次数字的不同的位。接下来,以结果中最右边的1所在的位数,来分组,
从而,可以将两个不同的数字划分到不同的分组中。
例如,{2,4,3,6,3,2,5,5},异或的结果是0010,以最右边1所在的位置划分的结果是{2,3,6,3,2}和{4,5,5}。
diff保存的是array数组中数字异或的结果.
*/
int diff = 0;
for (int num : array) {
diff ^= num;
}
//得到diff最右侧1的位置
diff = diff & (-diff);
//划分数组成两部分
for (int num : array) {
if ((num & diff) == 0)
num1[0] ^= num;
else
num2[0] ^= num;
}
}
}
56-2 数组中唯一只出现一次的数字
一个整型数组里除了1个数字只出现一次之外,其他的数字都出现了3次,找出只出现一次的数字。
public class AppearOnceInArray_56_2 {
public static int FindNumsAppearOnce(int[] array) throws Exception {
if (array == null || array.length == 0) {
throw new Exception("input error!");
}
//bitArray保存每个二进制位数组中元素相加的和
int[] bitArray = new int[32];
int bitMask = 1;
for (int i = 31; i >= 0; i--) {
for (int j = 0; j < array.length; j++) {
int bit = bitMask & array[j];
if (bit != 0) {
bitArray[i] += 1;
}
}
bitMask = bitMask << 1;
}
int res = 0;
//将res向右移1位,然后对每个二进制位上的数字对3求余。
for (int i = 0; i < 32; i++) {
res = res << 1;
res += bitArray[i] % 3;
}
return res;
}
public static void main(String[] args) throws Exception {
int[] arr = {1, 3, 3, 3, 2, 2, 2, 1, 1, 4, 4, 4, 9};
int res = FindNumsAppearOnce(arr);
System.out.println(res);
}
}
57-1 和为s的数字

牛客
题目描述
输入一个递增排序的数组和一个数字 S,在数组中查找两个数,使得他们的和正好是 S,如果有多对数字的和等于 S,输出两个数的乘积最小的。
输出描述
对应每个测试案例,输出两个数,小的先输出。
题解
使用两个指针,分别指向数组的第一个元素和最后一个元素。然后开始遍历,根据条件来移动指针。
import java.util.ArrayList;
public class SumToS_57_1 {
public ArrayList<Integer> FindNumbersWithSum(int[] array, int sum) {
int left = 0;
int right = array.length - 1;
int min = Integer.MAX_VALUE;
int res1 = 0;
int res2 = 0;
ArrayList arrayList = new ArrayList();
while (left < right) {
int curSum = array[left] + array[right];
if (curSum == sum) {
if (curSum < min) {
res1 = array[left];
res2 = array[right];
min = array[left] * array[right];
}
left++;
right--;
} else if (curSum > sum) {
right--;
} else {
left++;
}
}
if (min != Integer.MAX_VALUE) {
arrayList.add(res1);
arrayList.add(res2);
}
return arrayList;
}
public static void main(String[] args) {
SumToS_57_1 test = new SumToS_57_1();
int[] array = {1, 2, 3, 4, 5};
ArrayList<Integer> arrayList = test.FindNumbersWithSum(array, 10);
System.out.println(arrayList.toString());
}
}
57-2 和为s的连续正数序列

和57-1类似,这里使用small和big来表示序列的最大值和最小值,通过移动small和big的位置来
import java.lang.reflect.Array;
import java.util.ArrayList;
import java.util.Arrays;
public class SequenceSumToS_57_2 {
public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
int small = 1;
int big = 2;
ArrayList<ArrayList<Integer>> arrayLists = new ArrayList<>();
while (small <= (1 + sum) / 2) {
int curSum = getCurSum(small, big);
if (curSum == sum) {
ArrayList<Integer> arrayList = new ArrayList<>();
for (int i = small; i <= big; i++) {
arrayList.add(i);
}
arrayLists.add(arrayList);
big++;
} else if (curSum < sum) {
big++;
} else {
small++;
}
}
return arrayLists;
}
private int getCurSum(int small, int big) {
int curSum = (big - small + 1) * (small + big) / 2;
return curSum;
}
public static void main(String[] args) {
SequenceSumToS_57_2 test=new SequenceSumToS_57_2();
ArrayList<ArrayList<Integer>> arrayLists= test.FindContinuousSequence(90);
for (ArrayList<Integer> arrayList:arrayLists) {
System.out.println(arrayList.toString());
}
}
}
58-1 翻转单词顺序列
题目描述

Input:
"I am a student."
Output:
"student. a am I
题解
public class ReverseString_58_1 {
public String ReverseSentence(String str) {
if (str != null && str.length() != 0) {
char[] chars = str.toCharArray();
reverse(chars, 0, chars.length - 1);
int begin = 0;
int end = 0;
while (begin < chars.length) {
//划分单词,对每一个单词进行翻转
if (chars[end] == ' ' || end == chars.length - 1) {
int tmp_end = end;
if (chars[end] == ' ') {
tmp_end = end - 1;
}
reverse(chars, begin, tmp_end);
end++;
begin = end;
} else {
end++;
}
}
return String.valueOf(chars);
}
return str;
}
// 翻转字符串
public void reverse(char[] chars, int begin, int end) {
while (begin < end) {
char tmp = chars[begin];
chars[begin] = chars[end];
chars[end] = tmp;
begin++;
end--;
}
}
public static void main(String[] args) {
ReverseString_58_1 test = new ReverseString_58_1();
System.out.println(test.ReverseSentence("I am a student."));
// String str=null;
// String str1="";
// System.out.println(str.length());
// System.out.println(str1.length());
}
}
58-2 左旋转字符串

翻转三次,根据n把字符串分成两部分,然后分别对这两部分进行翻转,最后再对整个字符串进行翻转。
public class RotateLeft_58_2 {
public String LeftRotateString(String str, int n) {
//边界条件判断
if (str != null && str.length() != 0) {
if (n > 0 && n < str.length()) {
char[] chars = str.toCharArray();
reverse(chars, 0, n - 1);
reverse(chars, n, chars.length - 1);
reverse(chars, 0, chars.length - 1);
return String.valueOf(chars);
}
}
return str;
}
// 翻转字符串
public void reverse(char[] chars, int begin, int end) {
while (begin < end) {
char tmp = chars[begin];
chars[begin] = chars[end];
chars[end] = tmp;
begin++;
end--;
}
}
public static void main(String[] args) {
RotateLeft_58_2 test = new RotateLeft_58_2();
System.out.println(test.LeftRotateString("abcdefg", 2));
}
}
59-1 滑动窗口的最大值

import java.util.ArrayDeque;
import java.util.ArrayList;
public class MaxInWindows_59_1 {
public ArrayList<Integer> maxInWindows(int[] num, int size) {
ArrayList<Integer> res = new ArrayList<>();
if (num != null && num.length != 0) {
if (size > 0 && size <= num.length) {
int index = 0;
while (index + size <= num.length) {
int max = Integer.MIN_VALUE;
for (int i = index; i < size + index; i++) {
max = Math.max(max, num[i]);
}
res.add(max);
index++;
}
}
}
return res;
}
public ArrayList<Integer> maxInWindows_2(int[] num, int size) {
// 用一个双端队列,队列第一个位置保存当前窗口的最大值,每当窗口滑动一次,进行下面的判断:
// 1.判断当前最大值是否过期
// 2.新增加的值从队尾开始比较,把所有小于等于它的值从队列中移除,然后再添加新增的值
ArrayList<Integer> res = new ArrayList<>();
if (num != null && num.length != 0) {
if (size > 0 && size <= num.length) {
ArrayDeque<Integer> deque = new ArrayDeque<>();
int begin = 0;
for (int i = 0; i < num.length; i++) {
//begin记录滑动窗口的起始位置
begin = i - size + 1;
if (deque.isEmpty()) {
deque.addLast(i);
}
// 判断当前最大值是否过期
else if (begin > deque.peekFirst()) {
deque.pollFirst();
}
// 新增加的值从队尾开始比较,把所有小于等于它的值从队列中移除,然后再添加新增的值
while (!deque.isEmpty() && num[deque.peekLast()] <= num[i]) {
deque.pollLast();
}
deque.addLast(i);
// 添加当前滑动窗口的最大值
if (begin >= 0) {
res.add(num[deque.peekFirst()]);
}
}
}
}
return res;
}
}
59-2 队列的最大值

定义两个双端队列data和maxData,分别用来存储队列的元素和当前队列里的最大值。函数的实现和59-1类似。
import java.util.ArrayDeque;
public class MaxQueue_59_2 {
public class MaxQueue {
class InternalData {
int number;
int index;
public InternalData(int number, int index) {
this.number = number;
this.index = index;
}
}
ArrayDeque<InternalData> data;
ArrayDeque<InternalData> maxData;
int curIndex;
public MaxQueue() {
curIndex = 0;
}
public int max() throws Exception {
if (maxData.isEmpty()) {
throw new Exception("maxData is empty");
}
return maxData.pollFirst().number;
}
public void push_back(int number) {
while (!maxData.isEmpty() && maxData.peekLast().number <= number) {
maxData.pollLast();
}
InternalData internalData = new InternalData(number, curIndex);
data.addLast(internalData);
maxData.addLast(internalData);
curIndex++;
}
public void pop_front() throws Exception {
if (maxData.isEmpty()) {
throw new Exception("maxData is empty");
}
if (maxData.peekFirst() == data.peekFirst()) {
maxData.pollFirst();
}
data.pollFirst();
}
}
}
60 n个骰子的点数

import java.util.AbstractMap;
import java.util.ArrayList;
import java.util.List;
import java.util.Map;
public class DicesSum_60 {
//动态规划
public List<Map.Entry<Integer, Double>> dicesSum(int n) {
List<Map.Entry<Integer, Double>> res = new ArrayList<>();
// dp[i][j]表示前i个骰子产生点数j的次数
long[][] dp = new long[n + 1][6 * n + 1];
// 设置初始条件
for (int i = 1; i <= 6; i++) {
dp[1][i] = 1;
}
for (int i = 2; i <= n; i++) {
for (int j = 1 * i; j <= 6 * n; j++) {
for (int k = 1; k <= 6 && k <= j; k++) {
dp[i][j] += dp[i - 1][j - k];
}
}
}
double totalNum = Math.pow(6, n);
double p = 0;
for (int i = n; i <= 6 * n; i++) {
p = dp[n][i] / totalNum;
p = Double.valueOf(String.format("%.2f", p));
res.add(new AbstractMap.SimpleEntry<>(i, p));
}
return res;
}
//递归,时间复杂度较高
public List<Map.Entry<Integer, Double>> dicesSumByDiGui(int n) {
List<Map.Entry<Integer, Double>> res = new ArrayList<>();
double totalNum = Math.pow(6, n);
double p = 0;
long count = 0;
for (int i = n; i <= 6 * n; i++) {
count = getCount(n, i);
p = count / totalNum;
// 保留两位小数
p = Double.valueOf(String.format("%.2f", p));
res.add(new AbstractMap.SimpleEntry<>(i, p));
}
return res;
}
public long getCount(int num, int sum) {
if (num < 1 || sum > 6 * num || sum < num) {
return 0;
}
if (num == 1) {
return 1;
}
long count = getCount(num - 1, sum - 1) + getCount(num - 1, sum - 2)
+ getCount(num - 1, sum - 3) + getCount(num - 1, sum - 4)
+ getCount(num - 1, sum - 5) + getCount(num - 1, sum - 6);
return count;
}
public static void main(String[] args) {
DicesSum_60 test = new DicesSum_60();
List<Map.Entry<Integer, Double>> res = test.dicesSum(5);
for (Map.Entry<Integer, Double> map : res) {
System.out.println(map.toString());
}
}
}
61 扑克牌中的顺子

import java.util.Arrays;
public class ContinousCards_61 {
public boolean isContinuous(int[] numbers) {
if (numbers.length < 5) {
return false;
}
Arrays.sort(numbers);
//统计0的个数
int countZero = 0;
for (int i = 0; i < numbers.length; i++) {
if (numbers[i] == 0)
countZero++;
}
for (int i = countZero; i < numbers.length - 1; i++) {
//判断对子
if (numbers[i] == numbers[i + 1]) {
return false;
}
//用0填充缺失的数字
countZero = countZero - (numbers[i + 1] - numbers[i] - 1);
}
//最后只需判断0的个数是否大于等于0,小于0则说明缺失的数字用0去填补(或者数组中没有0)是不够的,因此是不连续的.
return countZero >= 0;
}
}
62 圆圈中最后剩下的数字

约瑟夫环问题:https://blog.csdn.net/u011500062/article/details/72855826
public class LastRemaining_62 {
//使用数组来模拟这个过程,这可以使用链表来模拟
public int LastRemaining_Solution(int n, int m) {
if (n == 0 || m == 0) {
return -1;
}
int[] arr = new int[n];
int count = n;
int index = 0;
while (count != 1) {
//找到第m个数
for (int i = 1; i < m; index++) {
if (index == n) {
index = 0;
}
while (arr[index] == 1) {
index++;
if (index == n) {
index = 0;
}
}
i++;
}
if (index == n) {
index = 0;
}
for (int i = index; i <= n; i++) {
if (i == n) {
i = 0;
}
if (arr[i] == 0) {
arr[i] = 1;
index = i;
break;
}
}
count--;
// System.out.print(index + " ");
}
System.out.println();
for (int i = 0; i < n; i++) {
if (arr[i] != 1) {
return i;
}
}
return -1;
}
// 约瑟夫环问题
// 递推公式:f(n,m)=(f(n-1,m)+m)%n
// 理解这个递推式的核心在于关注胜利者的下标位置是怎么变的。每杀掉一个人,其实就是把这个数组向前移动了 m 位。然后逆过来,就可以得到这个递推式。
public int LastRemaining_Solution_2(int n, int m) {
if (n == 0 || m == 0) {
return -1;
}
if (n == 1) {
return 0;
}
return (LastRemaining_Solution_2(n - 1, m) + m) % n;
}
public static void main(String[] args) {
LastRemaining_62 test = new LastRemaining_62();
System.out.println(test.LastRemaining_Solution(5, 3));
}
}
63 股票的最大利润

public class MaxProfit_63 {
public int maxProfit(int[] prices) {
if (prices == null || prices.length < 2) {
return 0;
}
// min表示前i只股票价格的最小值,maxProfile表示前i只股票获得的最大利润
int min = prices[0];
int maxProfit = prices[1] - prices[0];
for (int i = 1; i < prices.length; i++) {
maxProfit = maxProfit > prices[i] - min ? maxProfit : prices[i] - min;
if (prices[i] < min) {
min = prices[i];
}
}
if (maxProfit < 0) {
return 0;
}
return maxProfit;
}
public static void main(String[] args) {
MaxProfit_63 test = new MaxProfit_63();
int[] prices = {7, 1, 5, 3, 6, 4};
System.out.println(test.maxProfit(prices));
}
}
买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
计算连续递增的子序列之和,时间复杂度O(n)
public class MaxProfit_63_2 {
public int maxProfit(int[] prices) {
if (prices == null || prices.length < 2) {
return 0;
}
int maxProfit=0;
for (int i = 1; i < prices.length; i++) {
if(prices[i]>prices[i-1]){
maxProfit+=prices[i]-prices[i-1];
}
}
return maxProfit;
}
}
64 求 1+2+3+...+n
题目描述
要求不能使用乘除法、for、while、if、else、switch、case 等关键字及条件判断语句 A ? B : C。
65. 不用加减乘除做加法public class Sum_64 {
public int Sum_Solution(int n) {
int sum = n;
boolean b = (n > 0) && ((sum += Sum_Solution(n - 1)) > 0);
return sum;
}
}
65 不用加减乘除做加法
题目描述
写一个函数,求两个整数之和,要求不得使用 +、-、*、/ 四则运算符号。
解题思路
a ^ b 表示没有考虑进位的情况下两数的和,(a & b) << 1 就是进位。
递归会终止的原因是 (a & b) << 1 最右边会多一个 0,那么继续递归,进位最右边的 0 会慢慢增多,最后进位会变为0,递归终止。
public class Add_65 {
/*
链接:https://www.nowcoder.com/questionTerminal/59ac416b4b944300b617d4f7f111b215?f=discussion
来源:牛客网
首先看十进制是如何做的: 5+7=12,三步走
第一步:相加各位的值,不算进位,得到2。
第二步:计算进位值,得到10. 如果这一步的进位值为0,那么第一步得到的值就是最终结果。
第三步:重复上述两步,只是相加的值变成上述两步的得到的结果2和10,得到12。
同样我们可以用三步走的方式计算二进制值相加: 5-101,7-111 第一步:相加各位的值,不算进位,得到010,二进制每位相加就相当于各位做异或操作,101^111。
第二步:计算进位值,得到1010,相当于各位做与操作得到101,再向左移一位得到1010,(101&111)<<1。
第三步重复上述两步, 各位相加 010^1010=1000,进位值为100=(010&1010)<<1。
继续重复上述两步:1000^100 = 1100,进位值为0,跳出循环,1100为最终结果。
*/
public int Add(int num1, int num2) {
int res=num1^num2;
int flag=(num1&num2)<<1;
int tmp;
while(flag!=0){
tmp=res;
res=tmp^flag;
flag=(tmp&flag)<<1;
}
return res;
}
//递归
public int Add_1(int a, int b) {
return b == 0 ? a : Add(a ^ b, (a & b) << 1);
}
public static void main(String[] args) {
Add_65 test =new Add_65();
System.out.println(test.Add_1(111,899));
}
}
66 构建乘积数组
题目描述
给定一个数组 A[0, 1,..., n-1],请构建一个数组 B[0, 1,..., n-1],其中 B 中的元素 B[i]=A[0]A[1]...A[i-1]A[i+1]...A[n-1]。要求不能使用除法。
题解

public class Multiply_66 {
public int[] multiply(int[] A) {
if (A == null || A.length == 0) {
return A;
}
int[] B = new int[A.length];
int[] C = new int[A.length];
int[] D = new int[A.length];
C[0] = 1;
D[D.length - 1] = 1;
for (int i = 1; i < C.length; i++) {
C[i] = C[i - 1] * A[i - 1];
}
for (int i = D.length - 2; i >= 0; i--) {
D[i] = D[i + 1] * A[i + 1];
}
for (int i = 0; i < B.length; i++) {
B[i] = C[i] * D[i];
}
return B;
}
}
67 把字符串转换成整数
题目描述
将一个字符串转换成一个整数,字符串不是一个合法的数值则返回 0,要求不能使用字符串转换整数的库函数。
Iuput:
+2147483647
1a33
Output:
2147483647
0
注意边界条件的判断,数字不能超出Integer类型所能表示值的范围
public class StrToInt_67 {
public int StrToInt(String str) {
if (str == null || str.length() == 0) {
return 0;
}
char[] chars = str.toCharArray();
long res = 0;
boolean isNegative = str.charAt(0) == '-';
for (int i = 0; i < chars.length; i++) {
if (i == 0 && (chars[i] == '+' || chars[i] == '-')) {
continue;
}
if (chars[i] >= '0' && chars[i] <= '9') {
res += Math.pow(10, chars.length - i - 1) * (chars[i] - '0');
} else {
return 0;
}
}
res = isNegative ? -res : res;
if (res < Integer.MIN_VALUE || res > Integer.MAX_VALUE) {
return 0;
}
return (int) res;
}
public static void main(String[] args) {
StrToInt_67 test = new StrToInt_67();
System.out.println(test.StrToInt("-2147483648"));
// System.out.println(Integer.MAX_VALUE);
// System.out.println(Integer.MIN_VALUE);
}
}
68 二叉搜索树的最近公共祖先
给定一个二叉搜索树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
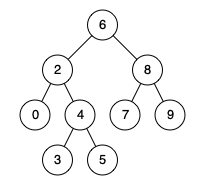
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
算法:
- 从根节点开始遍历树
- 如果节点 p和节点 q 都在右子树上,那么以右孩子为根节点继续 1 的操作
- 如果节点 p 和节点 q 都在左子树上,那么以左孩子为根节点继续 1 的操作
- 如果条件 2 和条件 3 都不成立,这就意味着我们已经找到节 p 和节点 q 的 LCA 了。
public class LowestCommonAncestor_68 {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){
return root;
}
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left,p,q);
}
if(root.val<p.val&&root.val<q.val){
return lowestCommonAncestor(root.right,p,q);
}
return root;
}
}
}