排序算法总结
最近在看左神的算法视频,随便记录下自己的学习心得,方便以后review,也让大家对基本的排序算法有个了解。
冒泡排序
冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
最简单的排序算法,实际工作中根本不会用到,因为时间复杂度为O(n^2),成本太高了。
排序过程
简单的说,就是两层循环的嵌套,给你n个数,每一次循环,排好一个最大或最小的数,重复上述这个过程,直到n-1次循环结束,就得到了从小到大排列的有序数列。
排序过程图解

关键代码:
public static void bubblesort(int[] arr) {
//第一种写法,每一次循环确定一个最大数
for (int i = 0; i < arr.length - 1; i++) { //循环的次数
for (int j = 0; j < arr.length - 1 - i; j++) { //比较的次数
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
// //第二种写法,每一次循环确定一个最小数
// for (int i = 0; i < arr.length - 1; i++) {
// for (int j = arr.length - 1; j > i; j--) {
// if (arr[j - 1] > arr[j]) {
// swap(arr, j - 1, j);
// }
// }
// }
}
//交换数组中两个数的位置
public static void swap(int[] arr, int m, int n) {
int t = arr[m];
arr[m] = arr[n];
arr[n] = t;
}
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
时间复杂度O(n^2),选择排序的优点主要与数据移动有关,对n个元素的排序最多进行n-1次交换。
排序过程图解
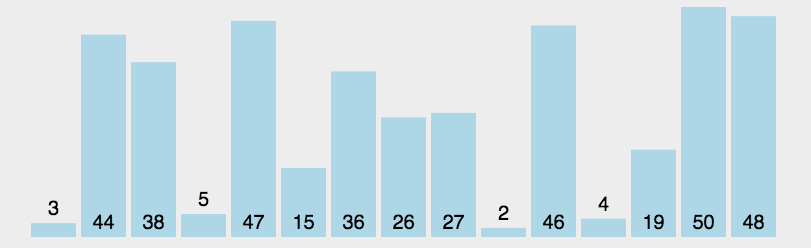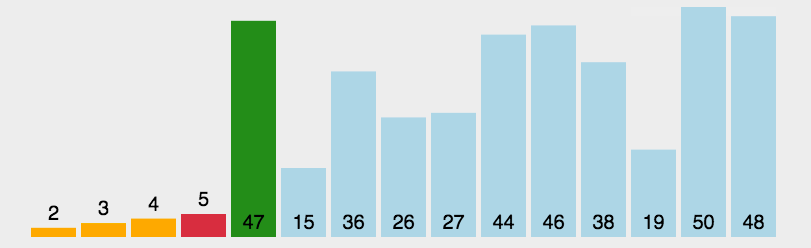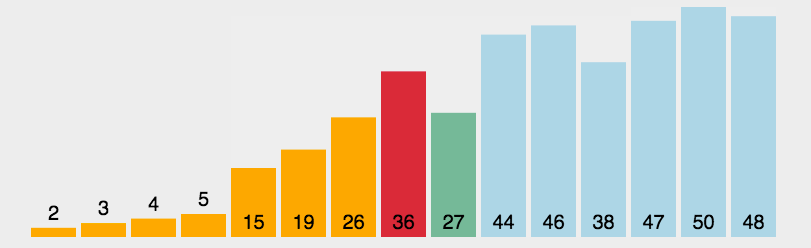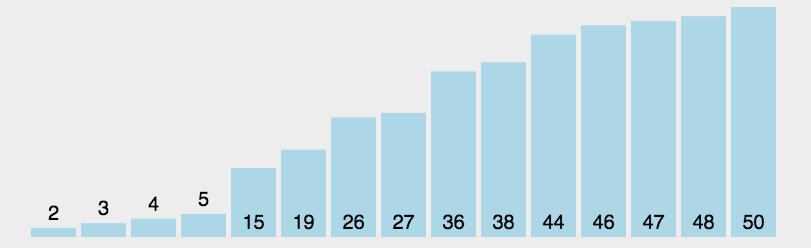
关键代码
public static void selectionsort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i; //记录最小值下标
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int m, int n) {
int t = arr[m];
arr[m] = arr[n];
arr[n] = t;
}
插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
时间复杂度为O(n^2)
排序过程图解

关键代码
public static void insertionsort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int m, int n) {
int t = arr[m];
arr[m] = arr[n];
arr[n] = t;
}
归并排序
归并排序(英语:Merge sort,或mergesort),是创建在归并操作上的一种有效的排序算法,效率为O(N*logN)(大O符号)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
时间复杂度为O(N*logN)
排序过程图解
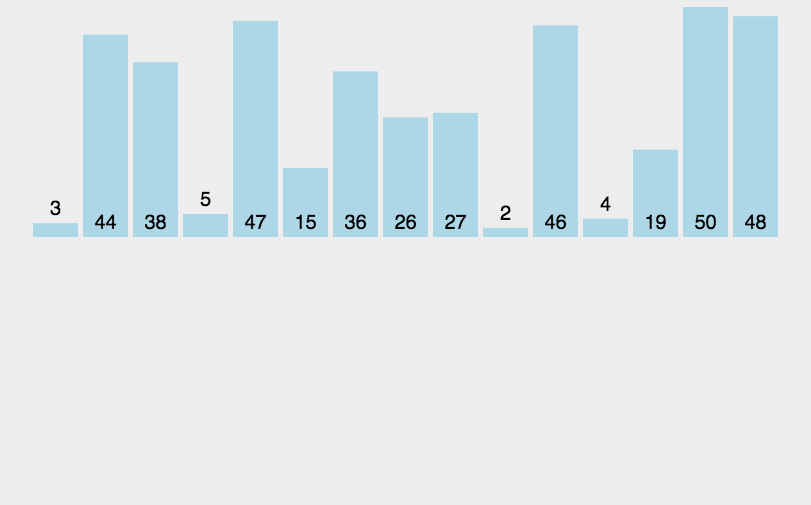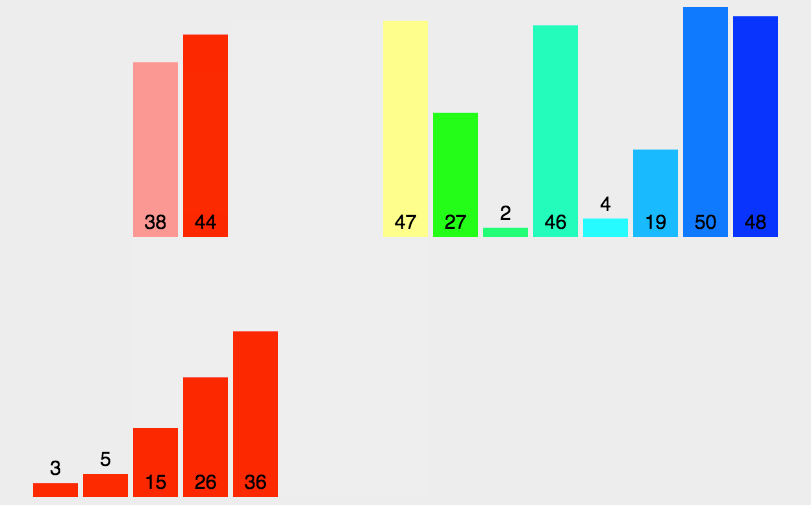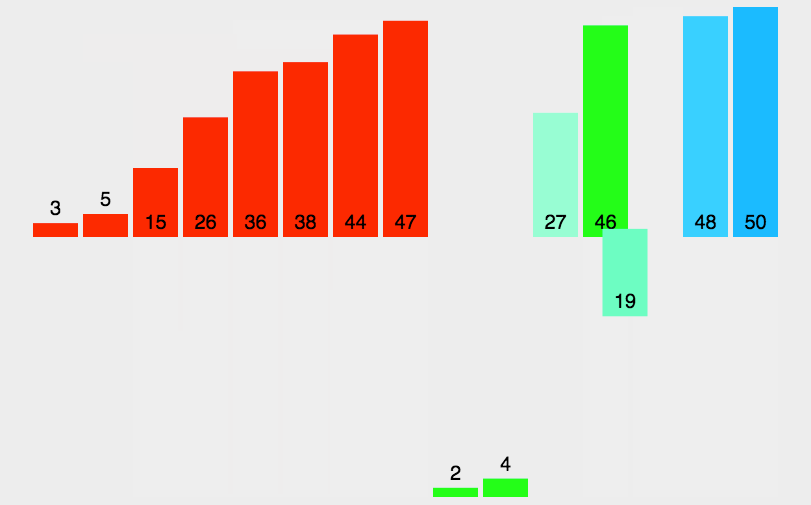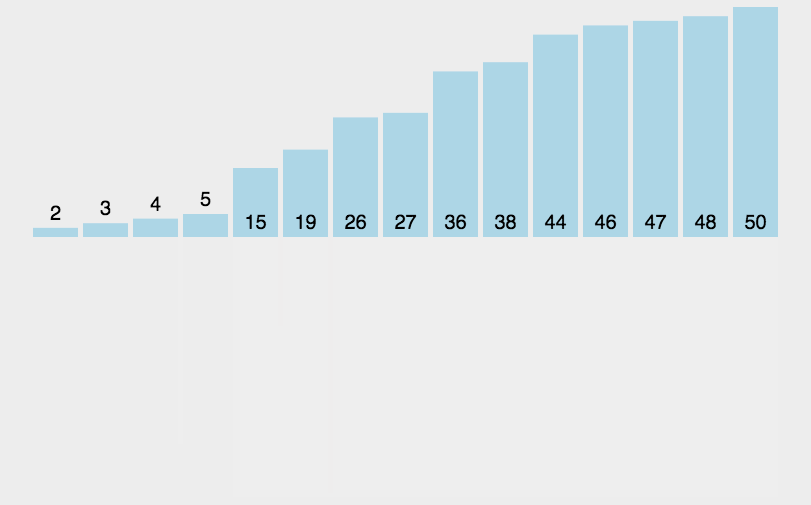
关键代码
//划分
public static void mergesort(int[] arr) {
if(arr==null||arr.length<2){
return;
}
mergesort(arr,0,arr.length-1);
}
public static void mergesort(int[] arr,int l,int r){
if(l==r){
return;
}
int mid=l+((r-l)>>1);
//划分成左右两块
mergesort(arr,l,mid);
mergesort(arr,mid+1,r);
//对左右两块进行排序并合并
merge(arr,l,mid,r);
}
//归并
public static void merge(int[] arr, int l, int m,int r) {
int[] tmp=new int[r-l+1]; //申请一个临时数组用来存储
int i=0;
int p1=l;
int p2=m+1;
while(p1<=m&&p2<=r){
tmp[i++]=arr[p1]<arr[p2]?arr[p1++]:arr[p2++];
}
//两个while只会执行一个
while(p1<=m){
tmp[i++]=arr[p1++];
}
while(p2<=r){
tmp[i++]=arr[p2++];
}
//将排好序的数组tmp复制到数组arr中
for(int j=0;j<tmp.length;j++){
arr[l+j]=tmp[j];
}
}
堆排序
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
时间复杂度为O(N*logN)
排序过程图解

关键代码
//堆排序
public static void heapsort(int[] arr) {
//数组为空或者长度为1直接返回
if(arr==null||arr.length<2){
return;
}
for(int i=0;i<arr.length;i++){
heapinsert(arr,i);
}
int size=arr.length;
//将堆顶元素和最后一个元素交换,然后再调整堆结构
swap(arr,0,--size);
while(size>0){
heapify(arr,0,size);
swap(arr,0,--size);
}
}
//往最大堆中插入数据
public static void heapinsert(int[] arr,int index) {
//孩子节点的值与双亲节点的值进行比较
while(arr[index]>arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index=(index-1)/2;
}
}
//调整最大堆的结构
public static void heapify(int[] arr,int index,int size) {
int left=2*index+1;
while(left<size){
//largest为最大值的下标
int largest=left+1<size&&arr[left+1]>arr[left]?left+1:left;
largest=arr[largest]>arr[index]?largest:index;
if(largest==index){
break;
}
swap(arr,largest,index);
index=largest;
left=2*index+1;
}
}
public static void swap(int[] arr, int m, int n) {
int t = arr[m];
arr[m] = arr[n];
arr[n] = t;
}
快速排序
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),简称快排,一种排序算法,最早由东尼·霍尔提出。在平均状况下,排序n个项目要O(nlogn)(大O符号)次比较。在最坏状况下则需要O(n^2)次比较,但这种状况并不常见。事实上,快速排序O(nlogn)通常明显比其他算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地达成。
时间复杂度为O(N*logN)
排序过程图解

关键代码
一般的写法:将左边第一个元素作为基准,每次从右往左找到第一个小于基准元素的下标,然后从左往右找到第一个大于基准元素的下标,最后,再交换这两个元素的值。重复上面的过程。
public static void quicksort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quicksort(arr, 0, arr.length - 1);
}
public static void quicksort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int tmp = arr[left];
int i = left;
int j = right;
while (i < j) {
while (arr[j] >= tmp && i < j) {
j--;
}
while (arr[i] <= tmp && i < j) {
i++;
}
if (i < j) {
swap(arr, i, j);
}
}
swap(arr, left, i);
quicksort(arr, left, i - 1);
quicksort(arr, i + 1, right);
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
进阶的写法:可以减少递归的次数,因为返回的区间不包含重复的元素。
例如,[3,1,2,3,3,4]
第一种写法,划分的区间是:[2,1]和[3,3,4]
第二种写法,划分的区间是:[2,1]和[4]
public static void quicksort(int[] arr) {
if(arr==null||arr.length<2){
return;
}
quicksort(arr,0,arr.length-1);
}
public static void quicksort(int[] arr,int l,int r){
if(l<r){
//随机挑选数组中的一个元素与右边的元素交换,时间复杂度为O(nlogn),叫做随机快排
swap(arr,l+(int)((r-l+1)*Math.random()),r);
int[] p=partion(arr,l,r);
quicksort(arr,l,p[0]);
quicksort(arr,p[1],r);
}
}
//返回以基准划分后的小于和大于基准边界的下标值
public static int[] partion(int[] arr,int l,int r){
//less表示小于基准的下标值
int less=l-1;
//刚开始让more指向数组最后一个元素,不参与下面的交换,最后要让其归位,more表示大于基准的下标值
int more=r;
//循环的条件l<more
while(l<more){
if(arr[l]<arr[r]){
swap(arr,++less,l++);
}else if(arr[l]>arr[r]){
swap(arr,l,--more);
}else{
l++;
}
}
//将基准元素归位
swap(arr,more,r);
return new int[]{less,more+1};
}
public static void swap(int[] arr, int m, int n) {
int t = arr[m];
arr[m] = arr[n];
arr[n] = t;
}
基数排序
基数排序(英语:Radix sort)是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数.
时间复杂度:O(d * (n + r))
排序过程图解

关键代码
public static void radixSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
//返回待排序数组的最大位数
public static int maxbits(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
}
int res = 0;
while (max != 0) {
res++;
max /= 10;
}
return res;
}
//digit:最大位数,
public static void radixSort(int[] arr, int begin, int end, int digit) {
final int radix = 10;
int i = 0, j = 0;
int[] count = new int[radix];
int[] bucket = new int[end - begin + 1];
for (int d = 1; d <= digit; d++) {
for (i = 0; i < radix; i++) {
count[i] = 0;
}
// 统计将数组中的数字分配到桶中后,各个桶中的数字个数
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);
count[j]++;
}
// 将各个桶中的数字个数,转化成各个桶中最后一个数字的下标索引
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
// 将原数组中的数字分配给辅助数组 bucket
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];
count[j]--;
}
/*
错误写法,会使得之前位数的排好的序混乱
for (i = begin; i<=end; i++) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];
count[j]--;
}
*/
//将bucket复制给arr
for (i = begin, j = 0; i <= end; i++, j++) {
arr[i] = bucket[j];
}
}
}
//返回对应位数上的数
public static int getDigit(int x, int d) {
return ((x / ((int) Math.pow(10, d - 1))) % 10);
}
计数排序
计数排序(Counting sort)是一种稳定的线性时间排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。
时间复杂度:O(n+k)
排序过程图解

关键代码
public static void countingsort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
}
int[] bucket = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
bucket[arr[i]]++;
}
int i = 0;
for (int j = 0; j < bucket.length; j++) {
while (bucket[j]-- > 0) {
arr[i++] = j;
}
}
}
排序算法性能比较



 浙公网安备 33010602011771号
浙公网安备 33010602011771号