2024.2 ~ 但不能请你喝咖啡
1. the 2nd ucup 20 G. Cola
假设已经确定了 LCP，那后面问一定是枚举 LCP 的下一位是什么，再往后的随便咋问都行。那就按照从小到大问 LCP 的下一位，再往后的从小到大排。这样问的次数就是逆序对数 +1。问题变为统计逆序对数 \(\leq m-1\) 的 \(n\) 阶排列个数。于是答案就是
分子只有 \(\mathcal{O}(\sqrt n)\) 项有值，\([x^k]\frac{1}{(1-x)^{n+1}}=\binom{n+k}{k}\)，直接算卷起来的第 \((m-1)\) 项就行。
2. ARC154E Reverse and Inversion
考虑 \(i\) 的贡献，假设 \(<p_i\) 的有 \(k\) 个放在 \(i\) 前面，那么 \(i\) 的贡献次数就是 \((i-1-k)-(p_i-1-k)=i-p_i\)，所以答案 \(f(p)=\sum_i(i^2-ip_i)\)，现在问题是求出 \(E(ip_i)\)。一次操作中如果操作了 \(i\)，那么 \(i\) 到 \(j,n-j+1\) 的概率是相同的（讨论一下就行），所以如果 \(p_i\) 被操作至少一次，那么它到每个位置的概率是相同的，所以其下标的期望为 \(\frac{n+1}{2}\)。
3. AGC056B Range Argmax
考虑让 \(x\) 对应唯一的 \(p\)，就从大到小将每个值填到尽可能靠左的位置。在 \(m\) 处填了 \(n\) 之后将包含这个位置的区间全都删掉，两侧递归下去，右侧是没有限制的，但是左侧要求所有位置都不能填 \(n\)。
假设左半部分最大值填在了 \(k\) 位置，如果没有区间同时包含 \(k,m\) 那么这个 \(m\) 就是不合法的，因为 \(n\) 可以再填到 \(k\) 位置；另一方面，有区间同时包含 \(k,m\)，首先 \(n\) 不能填到 \(k\)，其次左区间内部递归下去也保证了 \(k\) 是左区间内部第一个能填最大值的位置，继而 \(n\) 也不能填到其他位置（这一步是归纳说明）。
而现在 dp 就是有区间 \([l,r]\) 需要最大值位置 \(\geq k\) 的一个限制，直接 dp 就行。
4. AGC041F Histogram Rooks
直接顺着做就行。暴力是容斥枚举哪些格子不合法，那么它会 ban 掉同行同列，剩下的随便放就是 \(2\) 的次幂。再考虑枚举集合 \(S\) 中的列有 ban，对于每个行连续段，长为 \(cnt\)，包含了有 \(c=|S|\) 列有 ban，那么分为两种情况：它自己这一行没有被 ban 的，贡献是 \(2^{cnt-c}\)，否则是 \(\sum_{i=1}^c(-1)^i\binom{c}{i}=-[c>0]\)。
但是还有问题是有的列可能没有行去选它，所以在前者枚举 \(T\subseteq S\) 是没有被钦定无行选它的，容斥系数 \((-1)^{|S-T|}\)，也就是有 \(d=|T|\) 是可以选其作为 ban 的，从而两种情况的方案数是 \(2^{cnt-c}\) 和 \(-[d>0]\)。
行连续段的结构自然想到笛卡尔树，从最小值分开两边做，然后合并时再考虑最小值这一列是 “不选，仅在 \(S\) 中，同时在 \(S,T\) 中“ 三种情况的哪一种。
5. QOJ 5743 Palindromic Polynomial
如果我有罪请判罚我，而不是让我的大脑 H 区用更高的延迟才能对讲课人说的话做出反应。
回文多项式那么 \(A(x_i^{-1})x_i^d=A(x_i)\)，假如确定了 \(d\) 那么可以得出它经过 \((x_i^{-1},y_ix_i^{-d})\)，对这些点 \((x',y')\) 直接插值出来一个 \(A(x)\)，可能不满足系数回文，构造 \(B(x)=\frac{A(x)+A^R(x)}{2}\) 即可。这里有问题是如果插出来的系数常数项为 \(0\) 就有问题，它的实际度数会更小而不是想要的 \(d\)，那就先不管 \(x=0\) 的限制，最后再调整常数项（这里记得 check 如果常数项已经满足就不需要调整直接输出答案）。
假设 \((x',y')\) 一共有 \(m\leq 2n\) 个，得到 \(C(x)=\prod_{i=1}^m(x-x'_i)\)，满足对称就 \(D(x)=\frac{C(x)+C^R(x)}{2}\)。通过加上 \(D(x)\) 的若干倍来调整。那么就 \(m>d\) 一定不合法，否则进行调整（注意 \([x^0]C(x)\) 一定为 \(1\)，从而 \([x^0]D(x)\) 在 \(m=d\) 时是 2，否则是 1，总能对答案的常数项进行调整）。
那么现在就知道如何选取 \(d\)，假若给出的点值存在 \(x_ix_j=1\) 那么可以得到 \(x_i^d=z_i\) 这样的限制，在满足限制的 \(d\) 中找最大的去 check，否则选取 \(d=2n\) 就行（因为 \(m\leq 2n\)）。
实现上有好多细节/zk Code
6. CTT2023 D3T3（infoj 289）黄焖鸡
dp 套 dp。看内层 dp 咋搞，枚举左端点 \(l\)，然后 \(dp_{i,0/1}\) 表示 \(a_i\) 选没选，选了的方案减去没选的方案的最大值。如果 \(\max(dp_{i,0},dp_{i,1})>0\) 那么区间 \([l,i]\) 合法。转移式为 \(dp_{i,0}=\max(dp_{i-1,0},dp_{i-1,1})-a_i,dp_{i,1}=dp_{i-1,0}+a_i\)。
- 如果 \(dp_{i,1}<0\)，那么 \(\geq i\) 的右端点一定都合法，因为 \([l,i]\) 存在一个独立集不包含 \(i\) 且 \(>\) 整个区间和的一半，考虑 \([i+1,r]\) 中的奇数和偶数和至少有一大于等于 \([i+1,r]\) 的一半，拼起来就得到一个 \(>[l,r]\) 一半的独立集，也就是 \(\geq i\) 的右端点都合法。
- \(dp_{i,0}>0\) 同理，存在一个独立集不包含 \(i\) 且 \(>\) 整个区间和的一半。
- \(dp_{i,1}>\max a\)，在此方案中去掉 \(a_i\) 得到一个独立集不包含 \(i\) 且 \(>\) 整个区间和的一半。
- \(dp_{i,0}<-\max a\)，在不选的方案里面去掉 \(a_i\) 得到一个独立集不包含 \(i\) 且 \(>\) 整个区间和的一半。
综上，只需要考虑 \(dp_{i,0}\in [-\max a,0],dp_{i,1}\in [0,\max a]\)，此时转移时变为 \(dp_{i,0}=dp_{i-1,1}-a_i\)，从而可以得到这种情况下 \(dp_{i,0}+dp_{i,1}=0\)。那么需要记录的 \((dp_{i,0},dp_{i,1})\) 只有 19 个。外层 dp 的时候 \(dp_{i,T}\) 表示考虑完了前 \(i\) 位，每个左端点对应的 \((dp_{i,0},dp_{i,1})\) 集合是 \(T\)，这样复杂度就是 \(\mathcal{O}(n2^mm)\)。
假设 \(T\) 里面记的是 \(dp_{i,1}\) 出现了哪些值，那么转移相当于选取 \(x\in S_i,x\notin T\)，从集合 \(T\) 转移到集合 \(U=\{x-y\mid x>y,y\in T\}\)，那么可以从大到小枚举 \(x\)，然后 \(2^x\) 枚举所有 \(T\)，如果 \(T\) 中包含 \(x\) 那么就将 \(dp_{i,T}\to dp_{i,T-\{x\}}\)，否则转移 \(dp_{i,T}\to dp_{i,*}\)（相当于一个后缀和优化？）这样单次转移的复杂度降为了 \(\sum_{i=1}^m2^i=\mathcal{O}(2^m)\)。Code。
7. ARC156E Non-Adjacent Matching
找充要条件可能 tricky 一点，后面就是顺着一步步推...
一个序列合法的充要条件是 \(S=\sum X_i\) 是偶数，且任意的 \(X_i+X_{i+1}\leq S/2\)。必要性考虑如果不满足条件，那么无论怎么连边都不会使得条件变得满足，从而 \(S\) 不断减小至 \(=2\) 时不存在合法连边。充分性考虑对 \(X_i+X_{i+1}=S/2\) 的 \((i,i+1)\) 分布情况分类讨论（注意可以有 \((1,2),(2,3),(3,4)\) 这样的情况）总能找到一个合法的连边使得满足归纳条件。
计数考虑容斥。现在考虑 \(calc(0/1,n,m,k)\) 表示 \(\leq k\) 的奇/偶数个球放进 \(n\) 个可空盒子，每个盒子大小 \(\leq m\)，也就是 \((\frac{1-x^{m+1}}{1-x})^n\) 的奇/偶次项系数，\(\mathcal{O}(k/m)\) 枚举分子的系数之后，所有合法的分母系数和可以通过前缀和直接得到。
没有钦定的位置就是 \(calc(n,m,k)\)，钦定 \((1,2)\) 不合法就是枚举 \(X_1+X_2=i\)，后面的方案数是 \(calc(n-2,m,\min(i-1,k-i))\)，前面的方案数列下不等式看 \(X_1\) 合法取值个数。这部分时间复杂度毛估估是 \(\mathcal{O}(m)\times \mathcal{O}(k/m)=\mathcal{O}(k)\)。
钦定 \((1,2),(2,3)\) 不合法，枚举 \(X_2\) 大小是多少，再枚举 \(X_4+X_5+\cdots X_n=t\) 是多少，需要满足 \(t+X_3<X_1+X_2,t+X_1<X_2+X_3\)（所以这里枚举量是 \(\mathcal{O}(m^2)\) 的）。后面的方案数是 \(calc(n-3,m,t)-calc(n-3,m,t-1)\)，算出它们的复杂度是 \(\mathcal{O}(k)\)，前面的方案数是 \(\sum_{i=0}^m\sum_{j=0}^m[i+X_2>t+j][j+X_2>t+i][i+j+t+X_2\leq k][2|(i+j+t+X_2)]\)，整理下是 \(i+j\leq k-t-X_2, |i-j|<X_2-t\)，分奇偶维护一个 \(\mathcal{O}(m^2)\) 的二维前缀和就行。Code。
8. UOJ 84 水题走四方
如果两个人重叠了那么谁究竟是谁并没有区分，所以可以看作一个本体永远不会闪现，另一个分身可以闪现到本体处。那么最优方案一定是本体沿着一个叶子走，称走的这条链为主链。把分身会闪现回来的点称为关键节点，贪心肯定分身会把两个关键节点之间的主链外子树叶子走完，而且最后一次走最深的叶子，分身走最深的叶子的同时本体往下一个关键节点走。然后就可以直接得到 题解中 \(\mathcal{O}(n^2)\) 的 dp。
然后注意到 \(d_m[u,v]< d_v\) 的转移一定没有用，可以在走最深的叶子往回闪现的那个地方设一个关键点不劣（转移多了一种：如果自己是父亲唯一儿子那么 \(f[u]=f[fa]+1\)），类似的如果 \(d_m[u,v]\) 不是 \(d_m(u)\) 的话，最后往 \(d_m[u,v]\) 走的时候分身会和本体重合走一部分，把分叉点设为关键点不劣。所以需要的只是 \(d_m\) 在根链上的严格后缀最大值，单调栈大小至多是 \(\mathcal{O}(\sqrt n)\)，就得到了 \(\mathcal{O}(n\sqrt n)\) 的做法。
更进一步，其实只需要用栈顶更新，考虑 \(u_1\to u_2\to v\)，并且 \(d_m(u_1)>d_m(u_2)\geq d_v\)，设关键点 \(u_1,u_2,v\) 一定比只设关键点 \(u_1,v\) 要不劣，因为会同时下降的步数不变，但是“叶子到关键点距离和”减少。唯一的问题是单调栈弹栈是均摊的，所以需要二分弹栈以及记录原信息以复原。复杂度是 \(\mathcal{O}(n\log n)\)。
对于树上 mxdp 的单调栈考虑长链剖分，走轻儿子相当于把栈恢复到长链开头处，对于一条长链不断走重儿子可以暴力 pop 因为 pop 次数不超过长链长度。这个做法是线性的。
其实瓶颈还是在于对 \(v\) 找到最近的祖先 \(p_v\) 使得 \(v\) 的子树补 mxdp \(\geq\) \(v\) 子树 mxdp。注意一棵子树 \(u\) 中还没找到 \(p\) 的 mxdp 其实就是 \(mxdp_u\)，所以直接拿个链表记录还没找到 \(p\) 的点就行。
代码实现的是暴力 pop，但是先走长剖的轻儿子再走重儿子，需要手写递归栈避免 mle。Code。
9. CF750F New Year and Finding Roots
不难想到 1+2+3+4+5+6+7 的做法，就是问出两端是叶子的链然后往上爬。然后发现最后几步可以 bfs，所以就 1+2+3+4+(2^3-2)=10 了（最后 2^3-1 个点，如果问到最后一个点还没问到二度点那么最后一个点一定是二度点）。Code。
10. GDKOI 2023 异或图
\(m=0\) 就是枚举二进制位的一个前缀是都卡上界的，有一位开始松了，再往下就是随便选了。需要计算的就是这一位上是 \(1\) 的数选出奇/偶数个脱离上界，没脱离上界部分对方案数贡献是截取后面的位乘起来，脱离上界的 \(c\) 个对方案数贡献是 \((2^k)^{c-1}\)，拿个 \(f_{0/1/2}\) dp 算一下就行。
\(m>0\) 是互不相等容斥，对于每个在原图能连通的点集，需要计算它内部有多少边集能够使其连通，并且 \((-1)^{|E|}\) 容斥系数作为权值求和。计算出这个权值和，枚举 lowbit 和哪个子集相连，或者总方案数减去 lowbit 在某个子集连通块方案数，\(\mathcal{O}(3^n)\) 算就行。
现在就是将原图划分成若干能连通的子集，然后它们的容斥系数权值和相乘，再将每个大小为奇数的子集，其 \(\min\) 用 \(m=0\) 的做法算方案数。称作为奇数大小子集 \(\min\) 的点为关键点，对于每个关键点集合算方案数是 \(\mathcal{O}(2^nn\log C)\) 的。
暴力记录哪些点已经被选了，哪些点是关键点，这样状态数 \(\mathcal{O}(3^n)\)，加上转移的复杂度为 \(\mathcal{O}(4^n)\)。
优化就对 \(a\) 从小到大排序，每次加入集合时总加入还未出现的最小的 \(a\)，假设最小的没出现的是 \(i\)，对于 \(<a_i\) 的仅需要记录其是不是关键点，对于 \(\geq a_i\) 的仅需要记录其选没选。状态数降到 \(\mathcal{O}(n2^n)\)，加上转移的复杂度是 \(\mathcal{O}(n3^n)\)。Code。
11. 一个恒等式
组合意义：把 \(4n\) 个球，相邻的两个捆绑，捆成 \(2n\) 对球。\(C(2n,i)\) 是把两个都选的组，给选出来，\(C(2n-i, m-2i)\) 是把选了一个的组给选出来。
代数推导（by alpha1022）：
思路是用 gf 表示组合数凑二项式反演？
12. P8264 [Ynoi Easy Round 2020] TEST_100
序列分块，对每个块处理映射，用第二分块的套路，假设当前的值域是 \([L,R]\)，分类讨论 \(a\) 与 \(L,R,mid\) 的大小关系，用并查集和全局 tag 来维护映射。Code
13. P8860 动态图连通性
考虑实际上就是求出 \(1\sim n\) 的所有路径中，从小到大排序后字典序最大的那条路径是啥，除了这条路径以外的所有边都会被删掉。然后用主席树比较字典序跑 Dijkstra 就行。rqy 题解还有更强的结论，在 Dijkstra 每轮增广一个点的时候，选取权值最大的那个边增广就是对的。Code
14. Clamp Clamp Clamp
考虑整个过程相当于选一个起点和若干个区间，然后依次执行《如果在区间中就不变，不在区间中就移动到最近的端点》。考虑假设最后 \(k\) 个区间有交 \([l,r]\)，在倒数第 \((k+1)\) 个区间 \([l_{n-k},r_{n-k}]\) 之后无交，那么 \(l_{n-k}\leq r_{n_k}<l\leq r\) 的话 \(f(a)=l\)，否则是 \(r\)。
如果所有区间交起来非空，那么答案一定是 \(N\)，这种情况的方案数是 \((2n+1)(n!)^2\)（起点有 \(2n+1\) 种情况）
固定 \(k,l\) 计算 \(f(a)=l\) 方案数。后 \(k\) 对括号方案数是 \(l^{\underline{k-1}}(2n-l)^{\underline k}k\)，乘 \(k\) 是为了选出 \(l\) 是哪对括号。倒数第 \((k+1)\) 对括号的方案数是 \(\binom{l-k+1}{2}\)，还剩下 \((2n-2k-1)\) 个数，它们乱排的话，对于一个合法方案每一对括号可能排对或者排错，所以剩下的方案数是 \((2n-2k-1)!2^{-(n-k)}\)，大力化简得到 \(l!(2n-l)!2^{-(n-k)}k\binom{2n-2k-1}{l-k-1}\)。
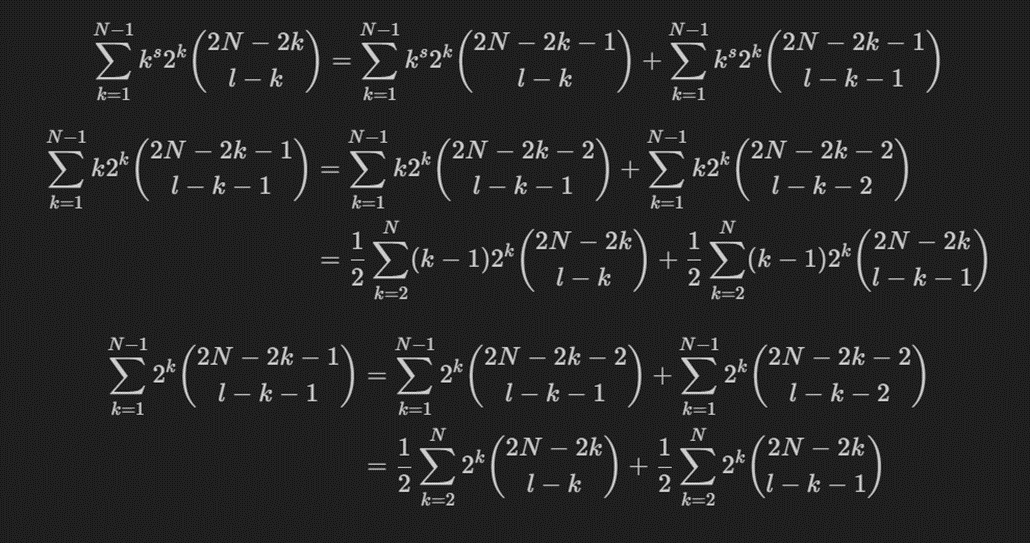
然后得到：
然后就能从 \(f(l+1,\ast,\ast)\) 得到 \(f(l,\ast,\ast)\)。
15. 一个恒等式
我咋还是不熟练把和式转为生成函数？先把右式写为 \(4^mn\frac{(n+m-1)!}{(2m)!(n-m)!}\)。
然后写成阶乘和右式同时约去 \(\frac{(n+m-1)!}{(2m)!}\)，再把右侧的 \(\frac{1}{(n-m)!}\) 乘到左边，现在式子两边是
把括号拆成 \((n+m)-k\) 之后 \(-k\) 的那部分吸收进去然后二项式定理就得到了右式。
16. ARC172D Distance Ranking
最开始将第 \(k\) 个点放到第 \(k\) 维坐标轴的极远处，令第 \(x\) 个点在第 \(y\) 维上的值，为 \(dis(x, y)\) 是所有距离中的第几大。
这个构造的思路是，最开始每个点在各自的坐标轴上，假设有 \(dis(x, y)<dis(x, z)\)，就让 \(x\) 在 \(y\) 那一维上的坐标微调一下 增大一丢丢。由于欧几里得距离是坐标差的平方，在非 \(x,y,z\) 轴上的微调对 \(dis(x, y)<dis(x, z)\) 这个不等式的影响非常小，这样就对了。Code
17. P6845 [CEOI2019] Dynamic Diameter
点分树，在每个分治中心处需要处理出它的儿子中，最大次大的子树 dep，加起来，更新答案。修改边权的时候跳点分树，对每个分治中心对叶子按 dfs 序维护线段树就行。这样做是两个 log。
原来还有更暴力的做法，直接线段树维护区间直径，考虑修改 \((x,y)\) 其中 \(y\) 是儿子子树区间是 \([l,r]\)，那么对线段树的影响就是所有和 \([l,r]\) 有交且不被 \([l,r]\) 包含的区间需要重新算，而在线段树上这样的区间不超过 \(\mathcal{O}(\log n)\) 所以直接做就是 \(\mathcal{O}(n\log ^2n)\) 的。
还有 1log 的做法，考虑欧拉序之后 \(dis(x,y)=dep_x-2\min(dep_y)+dep_z\) 其中 \(x\leq y\leq z\)（后面的 \(x,y,z\) 依然代指满足此条件的）。那么线段树维护分治信息只需要维护区间的 \(\max\{dep_x\},\min\{dep_x\},\max\{dep_x-2dep_y\},\max\{-2dep_x+dep_y\},\max\{dep_x-2dep_y+dep_z\}\)。修改相当于对 dep 进行区间加所以可以直接线段树。
这里唯一的问题在于合并的过程中 \(y\) 可能不是 \(LCA(x,z)\)，但注意到 \(LCA\) 的答案一定会更新到，并且不会比正确答案更优，所以是对的。这个复杂度是一个 log。Code。
18. AT_wtf19_b Multiple of Nine
令 \(S_i\) 为 \(i\) 位置的前缀和，然后可以连若干边表示这两个取值相同。对 \(l-1,r\) 离散化，注意到如果确定了所有 \(S\) 的取值，那么相邻两个 \(S\) 会有不同/相同两种系数的贡献方式（就是中间那些位有多少种取法，两边空出来的那些位置任意填）。而相同的可以直接缩点，于是可以建出一张 \(q\) 个点的图，每个点染 \([0,k=8]\) 其中一种颜色，有若干条边表示这两个点取值相同/不同会乘上的系数，求所有染色方案的总权值和。特别地最开头那个点必须染为 \(0\)。现在可以直接 \(\mathcal{O}(k3^q)\) 每次选出来当前颜色有哪些点。Code。
写成集合幂级数，其中需要求出 \(H=C^k\)，写成 \(H=\exp(k\ln(C))\) 就可以做到 \(\mathcal{O}(q^22^q)\) 了，这里实现的是一份 \(\mathcal{O}(3^q)\)：Code。
19. 2023-2024 集训队互测 不是这一道据数构结题
抽象做法。
需要观察到的是，排序做到第 \(i\) 个位置时上面放的数是前 \(i\) 个位置的最小值 \(pre_i\)。考虑固定左端点处理前缀询问，对于 \(pre=x\) 相同的一段 \([l,r]\)，\(l\) 从 \(l+1\) 往后找到第一个 \(>x\) 的位置 \(pos_l\)，再往后找到第一个 \(>x\) 的位置 \(pos_{l+1}\) ... 然后将所有 \(pos\) 处放一个 \(+1\) 的 tag，询问 \(r\) 就相当于 \(r\) 前面有多少 tag。
然后考虑 \(l\) 从大往小扫描线，怎么动态维护出这个 pos 和 tag。如果 \(a_l>a_{l+1}\)，说明新开了一段，直接二分找 \(pos_l\) 即可。\(a_l=a_{l+1}\) 就是从后面这一段最后的匹配位置往后再二分找 \(pos_l\)。
如果 \(a_l>a_{l+1}\)，它相当于推平 \(pre\) 后面的若干段为 \(a_l\)，后面有可能接上一段 \(pre=a_l\) 的段，假设后面第一个 \(\leq a_l\) 的位置是 \(R\)，那么可知 \([l,R-2]\) 中的每个位置 \(t\) 都重设为 \(pos_t=t+1\)，然后 \(R-1\) 再往后匹配。如果 \(R\) 这里是一个 \(pre\) 为 \(a_l\) 的段，我们发现次数相当于 \([R-1,?]\) 这一段中的所有点匹配对应往左换了，（\(x\) 的匹配点变成 \(x-1\) 的匹配点），难以动态维护。
但是对于 \(pre\) 相同的段，我们只需要保证它们打的 tag 没问题，以及最大 pos 没问题就行了，所以 \(R\) 那一段匹配位置不变，让 \(R-1\) 从 pos 最大位置往右二分找到匹配位置。
更进一步地，在最初的时候令 \(pos_t=t\) 而不是 \(t+1\)。让 \(l\) 从 pos 最大的位置往右二分找到匹配的位置，这样一段的最大 pos 就是左端点的 pos。
现在来看对 pos 的修改只有往左侧添加一个 pos，或者推平一段 \(pos_t=t\)，开个 vector 记录还没有被推平的 pos，用树状数组维护 tag 即可。
Code。
