「题解」Codeforces 1863G Swaps

看成内向基环森林，操作 $u\to v$ 相当于让 $u$ 连向 $v$ 所连的点，$v$ 变成自环。发现如果一个点 $v$ 变成了自环，那么操作任意一个 $u\to v$ 都没有用。

从简单的情形出发，对于一个内向树（或者说环大小为 $1$ 的内向基环树），每次操作 $x\to fa_x$ 时，相当于让 $fa_x$ 变成一个自环，然后 $x$ 的父亲就变成了 $fa_{fa[x]}$，并且 $fa_x$ 其它子树往上连的边再也不能跨过 $fa_x$．于是想到用树链剖分去对应操作出来的一张图。对于一条树链，让链底连向链顶的父亲，非链底的节点都是自环。

于是每次操作 $x$ 的时候，如果 $x$ 是链底并且链顶的父亲还没有重儿子，那么将链顶到父亲的这条边设为重边，否则什么也不干（对应 $x$ 是自环或 $x$ 连向了一个自环）。于是这样完成了链剖分方案与一张合法图方案的双射。这里有个问题是根已经是自环了，所以不能它不能有重边连下去。于是方案数就是除了根以外的度数 +1 之积 $\prod(d_i+1)$．

现在考虑环很大，依然想要让它去对应链剖分的情况。当环上全是重边的时候定义其表示环上所有点都是自环。

但是这个时候发现有计重的情况，当环上只有一条边不是重边的时候会出现这样的计重：

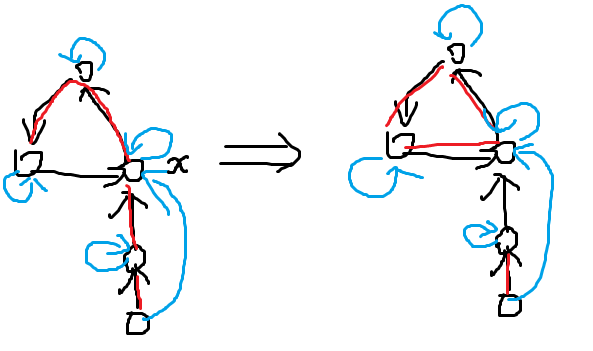
环上点的入边轻重选取方案将所有左侧的这种情况减去即可，也就是减去 $\sum_{u\in circle}d_u$．所以答案就是 $\prod_{circle}(\prod_{u\in circle}(d_u+1)-\sum_{u\in circle}d_u)\prod_{u\notin circle}(d_u+1)$