2019-2020 ICPC Southeastern European Regional Programming Contest (SEERC 2019)

A

题解

贪心怎么贪？假如要算 \(x\) 的答案，按照 \(x\) 为分界线拆分成若干段，对于每一段内部，再考虑形成了若干都 \(>x\) 和都 \(<x\) 的极长连续段。一个段内部大部分可以直接操作得到 \(x\)，但是在段和段的交界处需要多花一次操作让它和后面的相同才能再把它变成 \(x\)．这样就需要 \(n-cnt_x\) 再加上 \(>x\) 和 \(<x\) 的切换次数。

这样一定最优吗？发现如果有一个极长连续段长度为 1，那么它可以改成和左右两边相同的（同 \(>x\) 或者同 \(<x\)），从而用一次操作减少两次切换次数。而对于极长的一段 1，假设其长度为 \(len\)，那么这样就会少用 \((len+1)/2\) 次操作。

将 \(=x\) 的视作 0，\(>x\) 的视作 1，\(<x\) 的视作 -1。那么问题就变成了单点修改，查询有多少相邻的 1 -1（这个可以开个数组维护），以及极长连续单个蹦跶的 \((len+1)/2\) 的和（这个用线段树维护分治信息）。

B

题解

背包，\(f_{i,j,k}\) 表示前 \(i\) 个任务，丢个等级一的总经验是 \(j\)，丢给等级二的总经验是 \(k\)，最小时间是多少。

但是注意到会有经验溢出这件事，对于任意一个方案，做等级一的时候按照经验值从小往大加一定更优，所以背包的时候按照经验值从小往大插入，这样就能处理经验溢出的问题了。

C

题解

1 次询问问全局极差，再二分找到一个极长的前缀满足极差是全局极差，再问一次那个位置的值得到最值，再花一次询问确定这个位置是最大值还是最小值。这样一共 11 次询问。

然后对下标二进制分组，每次把这个位上是 1 的拉出来，询问这个集合得到 \(T\)，加上最值再询问得到 \(S\)，然后从 \(S-T\) 里面得到这些位置上的数（但是是无序的），再取个补集就是这一位是 0 的位置的数的集合。

对于每个位置，它每一位上都有一个可能的集合，交起来就是答案（1 和 0 都要看的）。

这样一共 11+2*8=27 次询问。

D

题解

• 如果只有一个字符，NO；
• 如果只有俩字符假设为 ab 且 a 出现次数更多。构造：n 个 a，1 个 b，剩余的 a，剩余的 b。只有 b 的个数 \(<2\) 的时候无解，需要特判 2n 是 2,4 的情况。
• 如果有仨字符，直接排序几乎是对的，只有众数出现次数 \(>n\) 的时候，需要随便找个字符插到第 \(n\) 个众数之后。

E

题解

令 \(l\) 是摩托车的下限，\(r\) 是司机的下限。枚举 \(p\) 个司机，然后贪心，现在问题就是计算最多剥削（ymh 老师用词精湛！）多少生命。

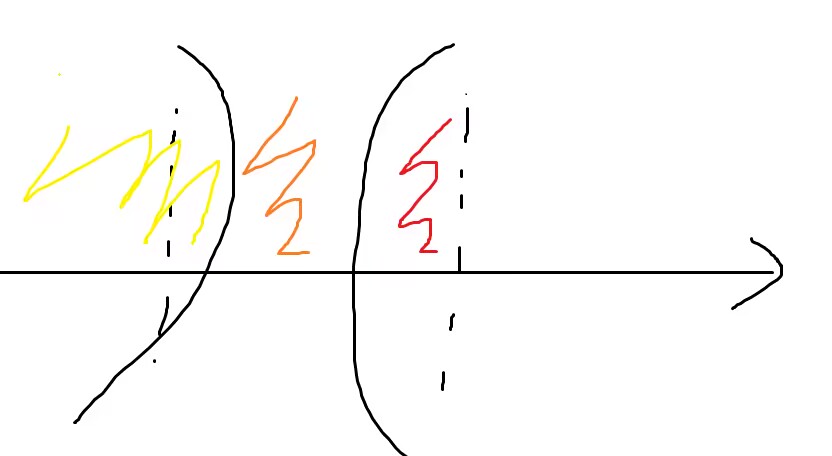
假设右侧大的是司机，左侧小的是乘客，中间的是摩托。黄色区域是查一下 \(\min(a_i-1, d)\) 的和，红色区域是要求都 \(>=r-d\)，查询 \(\max(0,r-a_i)\) 的和，橙色区域是查一下 \(\min(a_i-l,d)\) 的和。在值域上对出现次数以及 \(\sum a\) 都做个前缀和就能快速查了。

F

题解

是不是很像二分图博弈那个东西？当然这里是换成了无向图，不过结论是一样的。从 \(x\) 出发必胜当且仅当存在一个不包含 \(x\) 的最大匹配。起点能够随便选，那么后手必胜当且仅当对于所有的点 \(x\)，\(x\) 存在于任意一个最大匹配中，这玩意就等价于存在完美匹配。

树上祖先后代可以匹配，求最大匹配，经典问题。贪心一下，\(f_x\) 表示 \(x\) 子树内最少还剩多少个未匹配点就可以了。

G

题解

key point 是每层独立，然后就变成二维的问题。无解就是行列其中一个有 1，另一个无 1；最多就是行列有 1 的行和列相交点处都放个方块；最少就直接分行 1 个数和列 1 个数的大小关系然后贪心一下。

I

题解

考虑以 \(a_i\) 标记 \(b\) 中与 \(a_i\) 差的绝对最小的数（多个就随便标记一个）．每次删去一个 \(a_i\) 之后，至少会有一个 \(b\) 是不会被任意一个 \(a\) 标记的，那么这个数一定不会更优，直接删去即可。这样无论 \(a\) 留下哪个 \(a_i\)，\(b\) 都能让答案是 \(\min_{1\leq j\leq n}{|a_i-b_j|}\)，于是问题就变成最大化 \(\min_{1\leq j\leq n}{|a_i-b_j|}\)．把 \(a\) 和 \(b\) 放在一起排序，对每个 \(a_i\) 记录一下 \(a_i\) 前面第一个 \(b\) 和后面第一个 \(b\) 就行。

J

题解

考虑答案的下界，对于每个顶点考虑其作为中转点时的贡献，一定是最小和次小匹配，次次小和次次次小匹配...这个下界显然可以达到，实际上就是边权字典序最小的欧拉回路。