MSE,ks,mAP,weight decay等名词解释
参考链接:http://blog.sina.com.cn/s/blog_57a1cae80101bh65.html
均方误差 (Mean Squared Error)均方误差
MSE是网络的性能函数,网络的均方误差,叫"Mean Square Error"。比如有n对输入输出数据,每对为[Pi,Ti],i=1,2,...,n.网络通过训练后有网络输出,记为Yi。 在相同测量条件下进行的测量称为等精度测量,例如在同样的条件下,用同一个游标卡尺测量铜棒的直径若干次,这就是等精度测量。对于等精度测量来说,还有一种更好的表示误差的方法,就是标准误差。 标准误差定义为各测量值误差的平方和的平均值的平方根,故又称为均方误差。 设n个测量值的误差为ε1、ε2……εn,则这组测量值的标准误差σ等于:
数理统计中均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE
SSE(和方差、误差平方和):The sum of squares due to error
MSE(均方差、方差):Mean squared error
RMSE(均方根、标准差):Root mean squared error
R-square(确定系数):Coefficient of determination
Adjusted R-square:Degree-of-freedom adjusted coefficient of determination
下面我对以上几个名词进行详细的解释下,相信能给大家带来一定的帮助!!
一、SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式如下
SSE越接近于0,说明模型选择和拟合更好,数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗,所以效果一样
二、MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值,也就是SSE/n,和SSE没有太大的区别,计算公式如下
三、RMSE(均方根)
该统计参数,也叫回归系统的拟合标准差,是MSE的平方根,就算公式如下
在这之前,我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!!!
四、R-square(确定系数)
在讲确定系数之前,我们需要介绍另外两个参数SSR和SST,因为确定系数就是由它们两个决定的
(1)SSR:Sum of squares of the regression,即预测数据与原始数据均值之差的平方和,公式如下
(2)SST:Total sum of squares,即原始数据和均值之差的平方和,公式如下
细心的网友会发现,SST=SSE+SSR,呵呵只是一个有趣的问题。而我们的“确定系数”是定义为SSR和SST的比值,故
其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1],越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好
信用模型常用的评分标准:ks值, chi^2(卡方), iv
ks和roc曲线很像,具体理解如下:
ROC(Receiver Operating Characteristic Curve):接受者操作特征曲线。
ROC曲线及AUC系数主要用来检验模型对客户进行正确排序的能力。ROC曲线描述了在一定累计好客户比例下的累计坏客户的比例,模型的分别能力越强,ROC曲线越往左上角靠近。AUC系数表示ROC曲线下方的面积。AUC系数越高,模型的风险区分能力越强。
KS(Kolmogorov-Smirnov)检验:K-S检验主要是验证模型对违约对象的区分能力,通常是在模型预测全体样本的信用评分后,将全体样本按违约与非违约分为两部分,然后用KS统计量来检验这两组样本信用评分的分布是否有显著差异。
ROC值一般在0.5-1.0之间。值越大表示模型判断准确性越高,即越接近1越好。ROC=0.5表示模型的预测能力与随机结果没有差别。
KS值表示了模型将+和-区分开来的能力。值越大,模型的预测准确性越好。一般,KS>0.2即可认为模型有比较好的预测准确性。
要弄明白ks值和auc值的关系首先要弄懂roc曲线和ks曲线是怎么画出来的。其实从某个角度上来讲ROC曲线和KS曲线是一回事,只是横纵坐标的取法不同而已。拿逻辑回归举例,模型训练完成之后每个样本都会得到一个类概率值(注意是类似的类),把样本按这个类概率值排序后分成10等份,每一份单独计算它的真正率和假正率,然后计算累计概率值,用真正率和假正率的累计做为坐标画出来的就是ROC曲线,用10等分做为横坐标,用真正率和假正率的累计值分别做为纵坐标就得到两个曲线,这就是KS曲线。AUC值就是ROC曲线下放的面积值,而ks值就是ks曲线中两条曲线之间的最大间隔距离。由于ks值能找出模型中差异最大的一个分段,因此适合用于cut_off,像评分卡这种就很适合用ks值来评估。但是ks值只能反映出哪个分段是区分最大的,而不能总体反映出所有分段的效果,因果AUC值更能胜任。
https://www.zhihu.com/question/24529483
二、momentum是梯度下降法中一种常用的加速技术。对于一般的SGD,其表达式为
其中
三、normalization。如果我没有理解错的话,题主的意思应该是batch normalization吧。batch normalization的是指在神经网络中激活函数的前面,将
1、提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1],这样在反向传播时候的梯度都是在1左右,避免了梯度消失现象。
2、提升学习速率。归一化后的数据能够快速的达到收敛。
3、减少模型训练对初始化的依赖。
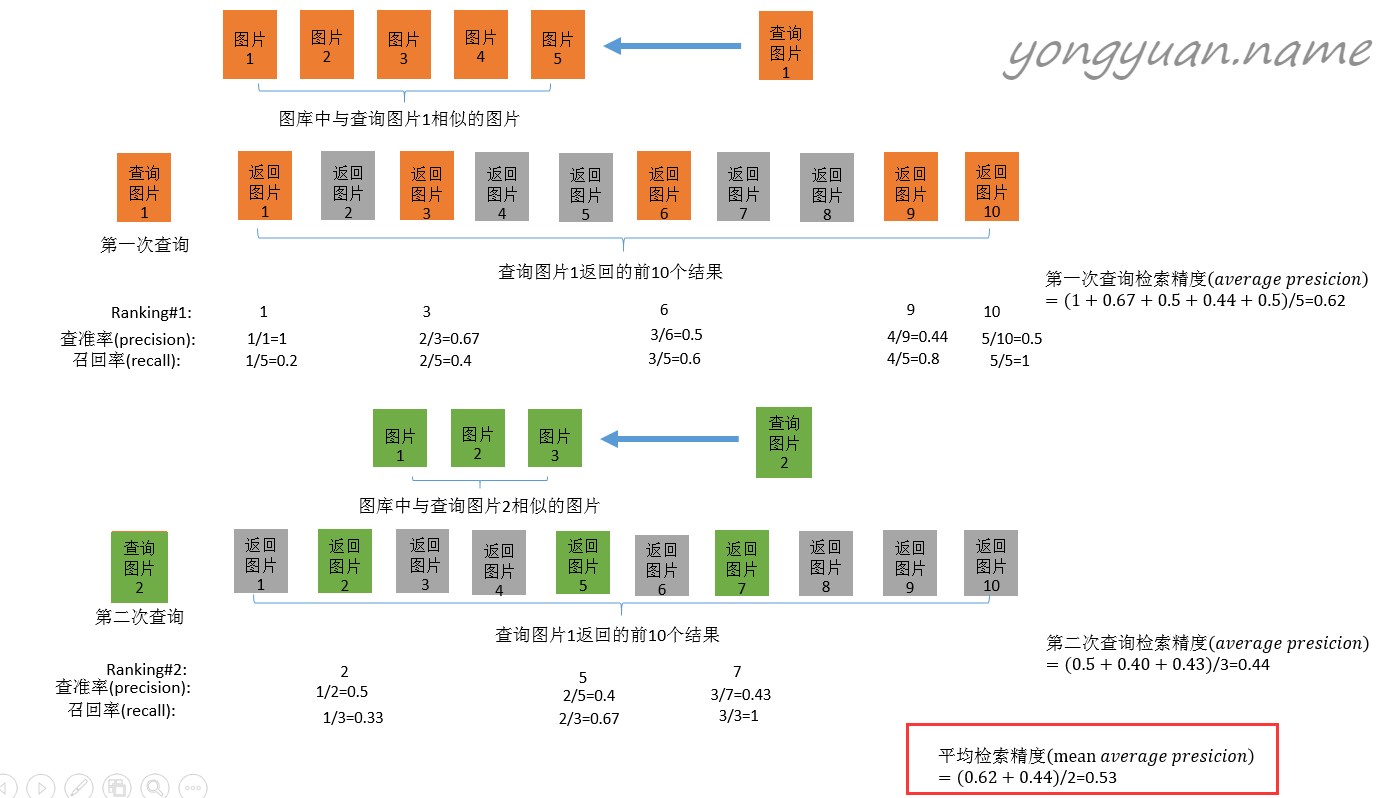
多标签图像分类(Multi-label Image Classification)任务中图片的标签不止一个,因此评价不能用普通单标签图像分类的标准,即mean accuracy,该任务采用的是和信息检索中类似的方法—mAP(mean Average Precision)。mAP虽然字面意思和mean accuracy看起来差不多,但是计算方法要繁琐得多,以下是mAP的计算方法:
首先用训练好的模型得到所有测试样本的confidence score,每一类(如car)的confidence score保存到一个文件中(如comp1_cls_test_car.txt)。假设共有20个测试样本,每个的id,confidence score和ground truth label如下:
接下来对confidence score排序,得到:
然后计算precision和recall,这两个标准的定义如下:
上图比较直观,圆圈内(true positives + false positives)是我们选出的元素,它对应于分类任务中我们取出的结果,比如对测试样本在训练好的car模型上分类,我们想得到top-5的结果,即:
在这个例子中,true positives就是指第4和第2张图片,false positives就是指第13,19,6张图片。方框内圆圈外的元素(false negatives和true negatives)是相对于方框内的元素而言,在这个例子中,是指confidence score排在top-5之外的元素,即:
其中,false negatives是指第9,16,7,20张图片,true negatives是指第1,18,5,15,10,17,12,14,8,11,3张图片。
那么,这个例子中Precision=2/5=40%,意思是对于car这一类别,我们选定了5个样本,其中正确的有2个,即准确率为40%;Recall=2/6=30%,意思是在所有测试样本中,共有6个car,但是因为我们只召回了2个,所以召回率为30%。
实际多类别分类任务中,我们通常不满足只通过top-5来衡量一个模型的好坏,而是需要知道从top-1到top-N(N是所有测试样本个数,本文中为20)对应的precision和recall。显然随着我们选定的样本越来也多,recall一定会越来越高,而precision整体上会呈下降趋势。把recall当成横坐标,precision当成纵坐标,即可得到常用的precision-recall曲线。这个例子的precision-recall曲线如下:
接下来说说AP的计算,此处参考的是PASCAL VOC CHALLENGE的计算方法。首先设定一组阈值,[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值(比如recall>0.3),我们都会得到一个对应的最大precision。这样,我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。
当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这N个样本中有M个正例,那么我们会得到M个recall值(1/M, 2/M, ..., M/M),对于每个recall值r,我们可以计算出对应(r' > r)的最大precision,然后对这M个precision值取平均即得到最后的AP值。计算方法如下:
相应的Precision-Recall曲线(这条曲线是单调递减的)如下:
AP衡量的是学出来的模型在每个类别上的好坏,mAP衡量的是学出的模型在所有类别上的好坏,得到AP后mAP的计算就变得很简单了,就是取所有AP的平均值。



