C4.5算法
一,C4.5算法是基于ID3算法的改进(优点)
- 对连续的数据也能处理
- 可以在决策树构造过程中进行剪枝,因为某些具有很少元素的结点可能会使构造的决策树过拟合(Overfitting),如果不考虑这些结点可能会更好
- 能够对不完整数据进行处理。
- 用信息增益率来进行属性选择的度量
二,算法流程
三,属性选择度量(和ID3对比)
属性选择度量又称分裂规则,因为它们决定给定节点上的元组如何分裂。属性选择度量提供了每个属性描述给定训练元组的秩评定,具有最好度量得分的属性被选作给定元组的分裂属性。目前比较流行的属性选择度量有--信息增益、增益率。 先做一些假设,设D是类标记元组训练集,类标号属性具有m个不同值,m个不同类Ci(i=1,2,…,m),CiD是D中Ci类的元组的集合,|D|和|CiD|分别是D和CiD中的元组个数。
-
信息增益
信息增益实际上是ID3算法中用来进行属性选择度量的。它选择具有最高信息增益的属性来作为节点N的分裂属性。该属性使结果划分中的元组分类所需信息量最小。对D中的元组分类所需的期望信息为下式:
Info(D)又称为熵。
现在假定按照属性A划分D中的元组,且属性A将D划分成v个不同的类。在该划分之后,为了得到准确的分类还需要的信息由下面的式子度量(条件熵):
信息增益定义为原来的信息需求(即仅基于类比例)与新需求(即对A划分之后得到的)之间的差,即
-
信息增益率
正是基于此,ID3后面的C4.5采用了信息增益率这样一个概念。信息增益率使用“分裂信息”值将信息增益规范化。分类信息类似于Info(D),定义如下:
这个值表示通过将训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。信息增益率定义:
选择具有最大增益率的属性作为分裂属性。
四,树剪枝
在决策树的构建的过程中,由于数据中的噪声和离群点,许多分枝反映的是训练数据中的异常。剪枝方法是用来处理这种过分拟合数据的问题。通常剪枝方法都是使用统计度量,剪去最不可靠的分枝。
-
先剪枝:
- 当决策树达到一定的高度就停止决策树的生长;
- 到达此节点的实例具有相同的特征向量,而不必一定属于同一类,也可以停止生长
- 到达此节点的实例个数小于某个阈值的时候也可以停止树的生长,不足之处是不能处理那些数据量比较小的特殊情况
- 计算每次扩展对系统性能的增益,如果小于某个阈值就可以让它停止生长。先剪枝有个缺点就是视野效果问题,也就是说在相同的标准下,也许当前扩展不能满足要求,但更进一步扩展又能满足要求。这样会过早停止决策树的生长。
-
后剪枝:
-
它由完全成长的树剪去子树而形成。通过删除节点的分枝并用树叶来替换它。树叶一般用子树中最频繁的类别来标记
五,具体举例
作者:奋斗的珞珞
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利.



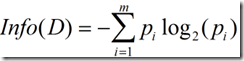
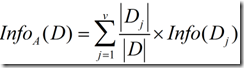
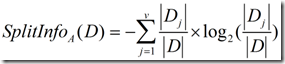
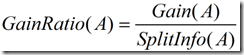

 浙公网安备 33010602011771号
浙公网安备 33010602011771号