决策模型(二):风险决策法
- 原文链接(转载请注明出处):决策模型(二):风险决策法

前言
风险决策法是指决策者对客观情况不了解,但是对将发生各事件的概率是已知的。决策者往往通过调查,根据过去的经验或主观估计等途径获得这些概率。在风险决策中一般采用期望值作为决策准则,常用的有最大期望收益决策准则(EMV)和最小机会损失决策准则(EOL)。
风险型决策问题一般具有以下特点:
- 决策具有明确目标: 获得最大收益(利润)或最小损失;
- 存在两个以上可供选择的行动方案
- 存在两个或两个以上不以决策者主观意志为转移的自然状态,但决策者根据过去的经验,主观估计或科学理论等可预先估算出这些状态出现的概率值;
- 各行动方案在确定状态下的损益值可以计算出来;
下面接着上一篇博文,对文中的例子做风险决策分析,决策矩阵如下:
| (策略\事件) | E1 = 0 | E2 = 10 | E3 = 20 | E4 = 30 | E5 = 40 |
|---|---|---|---|---|---|
| 事件概率(pj) | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
| S1 = 0 | 0 | 0 | 0 | 0 | 0 |
| S2 = 10 | -10 | 50 | 50 | 50 | 50 |
| S3 = 20 | -20 | 40 | 100 | 100 | 100 |
| S4 = 30 | -30 | 30 | 90 | 150 | 150 |
| S5 = 40 | -40 | 20 | 80 | 140 | 200 |
(注:记各自然状态发生的概率为\(p_j\),采用第 i 种方案在发生第 j 自然状态下的损益值为 \(a_{ij}\))
最大期望收益决策准则(EMV)
定义
最大期望收益决策,显而易见,就是计算出每个方案期望收益值,然后选取最大期望值对应的方案即为最优方案。
计算步骤
先根据各事件发生的概率 \(p_j\),求出各个策略的期望收益值。然后从这些期望收益值中选择最大者,它对应的策略为决策应选策略。
计算公式
S*k \(\rightarrow\) max \(\sum_{j} p_ja_{ij}\)
计算结果
| (策略\事件) | E1 = 0 | E2 = 10 | E3 = 20 | E4 = 30 | E5 = 40 | EMV |
|---|---|---|---|---|---|---|
| 事件概率(pj) | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 | |
| S1 = 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S2 = 10 | -10 | 50 | 50 | 50 | 50 | 44 |
| S3 = 20 | -20 | 40 | 100 | 100 | 100 | 76 |
| S4 = 30 | -30 | 30 | 90 | 150 | 150 | 84 \(\longleftarrow\) max |
| S5 = 40 | -40 | 20 | 80 | 140 | 200 | 80 |
根据 EMV 决策准则有
max (0 , 44 , 76, 84, 80) = 84
对应的决策策略为 S4,为决策者选择的策略。
EMV 决策准则适用于一次决策多次重复进行生产的情况,所以它是平均意义下的最大收益。
计算代码
private static int row = 4; //行
private static int col = 3; //列
private static double t =2; //效用曲率系数
private static double[][] matrix = {//决策矩阵
//事件 1 2 3
{0.2,0.5,0.3}, //事件概率
{140,120, 80}, //策略
{200,150, 40}, //策略
{340,140,-20}, //策略
};
/**
* 最大期望收益决策准则(EMV)
* @param matrix
* @param row
* @param col
*/
private static void EMV(double[][] matrix, int row, int col){
double[] maxMar = new double[row+1]; //记录每种行动方案的结果,第一行是自然状态概率
double max = 0.0; //最优结果
double temp = 0.0;
double chance = 0.0; //概率
int maxIndex = 0; //最优结果下标
//因为第一行是自然状态概率,所以从第二行开始,实际的行数比 row 多一行
for (int i = 1; i <= row; i++) {
for (int j = 0; j < col; j++) {
chance = matrix[0][j]; //自然概率
temp = (j != 0) ? (temp + matrix[i][j]*chance) : (matrix[i][j]*chance);
}
maxMar[i] = temp;
if(i == 1){ // 当 i=1时,为 max 与 maxIndex 赋初值
max = temp;
maxIndex = 1;
}else if(temp > max){
max = temp;
maxIndex = i;
}
}
System.out.println(Arrays.toString(maxMar));
System.out.println(max+"--"+maxIndex);
}
最小机会损失决策准则(EOL)
定义
最小机会损失决策与不确定型决策法里的最小机会损失决策准则相类似,都是先将收益矩阵的中各元素变换为机会损失值。将各自然状态下的最大收益值定为理想目标,并将该状态中的其他值与最高值之差称为机会损失值。然后求这些机会损失值的期望损失值,最后从中选取最小的期望损失值,对应的策略即为决策者所选的策略。
计算步骤
首先计算出当发生 j 事件后,各策略的收益最大值
aij = max ( aij )
这时各策略的机会损失值为
\(a'_{ij}\) = { max ( aij ) - aij }
然后求这些机会损失值的期望损失值,最后从中选取最小的期望损失值
min \(\sum_{j} p_ja'_{ij}\)
计算公式
S*k \(\rightarrow\) min \(\sum_{j} p_ja'_{ij}\)
计算结果
| (策略\事件) | E1 = 0 | E2 = 10 | E3 = 20 | E4 = 30 | E5 = 40 | EOL |
|---|---|---|---|---|---|---|
| 事件概率(pj) | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 | |
| S1 = 0 | 0 | 50 | 100 | 150 | 200 | 100 |
| S2 = 10 | 10 | 0 | 50 | 100 | 150 | 56 |
| S3 = 20 | 20 | 10 | 0 | 50 | 100 | 24 |
| S4 = 30 | 30 | 20 | 10 | 0 | 50 | 16 \(\longleftarrow\) max |
| S5 = 40 | 40 | 30 | 20 | 10 | 0 | 20 |
根据 EOL 决策准则有
min (100, 56 , 24, 16, 20) = 16
对应的决策策略为 S4,为决策者选择的策略。
从本质上讲 EMV 与 EOL 决策准则是一样的。所以决策时这两个决策结果是一样的。
计算代码
/**
* 最小机会损失决策准则(EOL)
* @param matrix
* @param row
* @param col
*/
private static void EOL(double[][] matrix, int row, int col){
//先求损失矩阵
double[][] loss = new double[row+1][col];
for (int j = 0; j < col; j++) {
loss[0][j] = matrix[0][j]; //将自然概率复制到损失矩阵的第一行中
double max = matrix[1][j]; //先定每一列的第一个最大
for (int i = 1; i <= row; i++) {
if(matrix[i][j] > max){
max = matrix[i][j];
}
}
//此时已经求出该列的最大值
//损失矩阵中对应位置的值 = 决策矩阵中列最大值 - 决策矩阵中对应位置值
for (int i = 1; i <= row; i++) {
loss[i][j] = max - matrix[i][j];
}
}
//然后再求 EOL 决策
double[] maxMar = new double[row+1];
double min = 0.0;
double temp = 0.0;
int minIndex = 0;
double chance = 0.0;
for (int i = 1; i <= row; i++) {
for (int j = 0; j < col; j++) {
chance = loss[0][j]; //自然概率
temp = (j != 0) ? (temp + loss[i][j]*chance) : (loss[i][j]*chance);
}
maxMar[i] = temp;
if(i == 1){
min = temp;
minIndex = 1;
} else if(temp < min){
min = temp;
minIndex = i;
}
}
System.out.println(Arrays.toString(maxMar));
System.out.println(min+"--"+minIndex);
}
全情报的价值(EVPI)
定义
当决策者耗费了一定经费进行调研,获得了各事件发生概率的信息,应采用 ”随机应变“ 的战术,这时所得的期望收益称为全情报的期望收益,记做 EPPI,这个收益应当大于至少等于最大期望收益,即 EPPI >= max(EMV),则有EVPI = EPPL - max(EMV),EVPI 称为全情报的价值,这就说明获得情报的费用不能超过 EVPI 值,否则就没有增加收入。
计算步骤
先进行 EMV 决策法计算,求得最大期望收益值
max \(\sum_{j} p_ja_{ij}\)
然后求全情报期望收益,先得求收益矩阵中每行的最大值然后求期望,最后将每行最大值的期望相加,得到全情报期望收益。
\(\sum_{j} p_jmax(a_{i})\) ; \(max(a_{i})\) 是 i 行的最大值
全情报期望收益减去最大期望收益即为全情报价值 EVPI
EVPI = \(\sum_{j} p_jmax(a_{i})\) - max \(\sum_{j} p_ja_{ij}\)
计算公式
EVPI = \(\sum_{j} p_jmax(a_{i})\) - max \(\sum_{j} p_ja_{ij}\)
计算结果
| (策略\事件) | E1 = 0 | E2 = 10 | E3 = 20 | E4 = 30 | E5 = 40 | EMV | 期望收益 | EVPI |
|---|---|---|---|---|---|---|---|---|
| 事件概率(pj) | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 | |||
| S1 = 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| S2 = 10 | -10 | 50 | 50 | 50 | 50 | 44 | ||
| S3 = 20 | -20 | 40 | 100 | 100 | 100 | 76 | ||
| S4 = 30 | -30 | 30 | 90 | 150 | 150 | 84 \(\longleftarrow\) max | 100 | 16 |
| S5 = 40 | -40 | 20 | 80 | 140 | 200 | 80 |
根据 EMV 决策准则有
max (0, 44, 76 , 84, 80) = 84
得到最大的期望收益值为 84 , 再求得全情报期望收益 = 100 ,最后可得全情报价值EVPI = 16, 对应的决策策略为 S4,为决策者选择的策略。
计算代码
/**
* 全情报价值(EVPI)
* @param matrix
* @param row
* @param col
*/
private static void EVPI(double[][] matrix, int row, int col){
double[] maxMar = new double[row+1]; //记录每种行动方案的结果,第一行是自然状态概率
double max = 0.0; //最优结果
double temp = 0.0;
double chance = 0.0; //概率
int maxIndex = 0; //最优结果下标
//因为第一行是自然状态概率,所以从第二行开始,实际的行数比 row 多一行
for (int i = 1; i <= row; i++) {
for (int j = 0; j < col; j++) {
chance = matrix[0][j]; //自然概率
temp = (j != 0) ? (temp + matrix[i][j]*chance) : (matrix[i][j]*chance);
}
maxMar[i] = temp;
if(i == 1){ // 当 i=1时,为 max 与 maxIndex 赋初值
max = temp;
maxIndex = 1;
}else if(temp > max){
max = temp;
maxIndex = i;
}
}
double rowMax = 0.0;
double expect = 0.0;
double chance = 0.0;
double value = 0.0;
//计算全情报价值收益
for (int i = 0; i < col; i++) {
chance = matrix[0][i]; //自然概率
for (int j = 1; j <= row; j++) {
if(j == 1){ //初始化第一行第一个为该行最大的收益值
rowMax = matrix[j][i];
}else if (matrix[j][i] > rowMax){
rowMax = matrix[j][i];
}
}
expect += rowMax * chance;
}
except = new BigDecimal(expect).setScale(2, BigDecimal.ROUND_HALF_UP).doubleValue();
value = new BigDecimal(expect - max).setScale(2, BigDecimal.ROUND_HALF_UP).doubleValue();
System.out.println("全情报期望收益:"+except);
System.out.println("全情报价值EVPI:"+value);
}
效用曲线拟合(EUV)
定义
效用概念首先是由贝努里提出的,他认为人们对其钱财的真实价值的考虑与他的钱财拥有量有对数关系。经济管理学家将效用作为指标,用它来衡量人们对某些事物的主观价值,态度,偏爱,倾向等。例如在风险情况下进行决策,决策者对风险的态度是不同的,用效用指标来量化决策者对待风险的态度,可以给每一个决策者测定他对待风险的态度的效用曲线函数。这里还有一个概率是效用曲线系数,效用曲线系数的取值范围为(0,∞)。
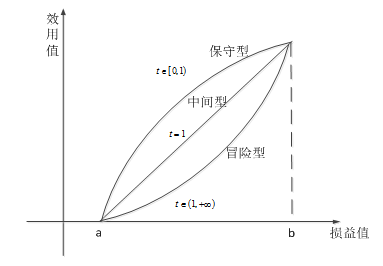
计算步骤
先建立效用曲线函数,将矩阵中的收益值装化为效用值,其中 t 为效用曲线系数,b=max{x1,x2,x3,⋯,xn} ,a=min{x1,x2,x3,⋯,xn}) ;
U(x) = \(\left\{\begin{matrix} &0, & x\leq a & \\ &(\frac{x-a}{b-a})^t, & a\leq x\leq b \\ &1, &x\geq b \end{matrix}\right.\)
然后计算期望效用值,结果为期望效用的最大值
EUVi = \(\sum_{j} p_ju_{ij}\)
计算公式
S*k \(\rightarrow\) max \(\sum_{j} p_ju_{ij}\)
计算结果
| (策略\事件) | E1 = 0 | E2 = 10 | E3 = 20 | E4 = 30 | E5 = 40 | EUV(t=2) |
|---|---|---|---|---|---|---|
| 事件概率(pj) | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 | |
| S1 = 0 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 |
| S2 = 10 | 0.02 | 0.14 | 0.14 | 0.14 | 0.14 | 0.128 |
| S3 = 20 | 0.01 | 0.11 | 0.34 | 0.34 | 0.34 | 0.261 |
| S4 = 30 | 0.0 | 0.09 | 0.29 | 0.63 | 0.63 | 0.323 |
| S5 = 40 | 0.0 | 0.06 | 0.25 | 0.56 | 1.0 | 0.324 \(\longleftarrow\) max |
根据 EUV决策准则有
max (0.03, 0.128 , 0.261, 0.323, 0.324) = 0.324
对应的决策策略为 S5,为决策者选择的策略。
计算代码
/**
* 效用曲线拟合(EUV)
* @param matrix
* @param row
* @param col
*/
private static void EUV(double[][] matrix, double a, int row, int col){
//先求出收益矩阵中的最大值与最小值
double min = matrix[1][0];
double max = matrix[1][0];
for (int i = 2; i < row; i++) {
for (int j = 0; j < col; j++) {
if(matrix[i][j] > max){
max = matrix[i][j];
}
if(matrix[i][j] < min){
min = matrix[i][j];
}
}
}
System.out.println("min="+min+"max="+max);
//然后求出效用值矩阵
/*计算方法
小于最小值(a) => 0
大于最大值(b) => 1
介于之间=> (x-a/b-a)^t,其中t为效用曲线系数
*/
double[][] avail = new double[row+1][col];
for (int i = 1; i <= row; i++) {
for (int j = 0; j < col; j++) {
avail[0][j] = matrix[0][j]; //将自然状态概率复制到第一行中
if(matrix[i][j] <= min){
avail[i][j] = 0.0;
}else if(matrix[i][j] >= max){
avail[i][j] = 1.0;
}else {
double pow = Math.pow((matrix[i][j] - min) / (max - min), t);
avail[i][j] = new BigDecimal(pow).setScale(2, BigDecimal.ROUND_HALF_UP).doubleValue();
}
}
}
for (int i = 0; i < row; i++) {
System.out.println(Arrays.toString(avail[i]));
}
//再求期望效用值
double[] maxMar = new double[row+1];
double availMax = 0.0; //效用期望最大值
int maxIndex = 0;
double temp = 0.0;
double chance = 0.0;
for (int i = 1; i <= row; i++) {
for (int j = 0; j < col; j++) {
chance = avail[0][j]; //自然概率
temp = (j != 0) ? (temp + avail[i][j]*chance) : (avail[i][j]*chance);
}
double value =new BigDecimal(temp).setScale(3, BigDecimal.ROUND_HALF_UP).doubleValue();
maxMar[i] = value;
if(i == 1){
availMax = value;
maxIndex = 1;
} else if(value > availMax){
availMax = value;
maxIndex = i;
}
}
System.out.println(Arrays.toString(maxMar));
System.out.println(availMax+"--"+maxIndex);
}
总结
至此,决策模型模块的所有算法模型都分析,建立并实现完成。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号