[swarthmore cs75] Lab 1 — OCaml Tree Programming
课程回顾
Swarthmore学院16年开的编译系统课,总共10次大作业。本随笔记录了相关的课堂笔记以及第2大次作业。
比较两个lists的逻辑:
let rec cmp l ll =
match (l,ll) with
| [], [] -> 0
| [],_ -> -1
| _,[] -> 1
| (h::t), (hh::tt) -> if h > hh then 1
else if h < hh then -1
else cmp t tt;;
编程作业
1. 平衡二叉树(AVL tree)
- 一颗AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树(空树的高度定义为-1)。
在进行插入时,有四种情况会破坏树的平衡性质,需要通过相应的旋转操作来恢复树的平衡。这四种情况如下所示:- 情况一:对左儿子的左子树进行一次插入(通过单旋转恢复平衡)
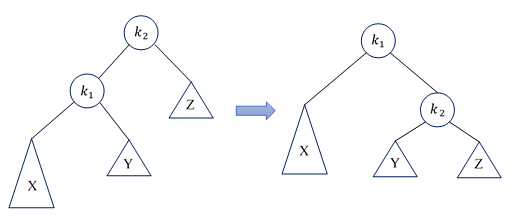
- 情况一:对左儿子的左子树进行一次插入(通过单旋转恢复平衡)
if k2左子树高度 - k2右子树高度 = 2 > 1 then
RotateLeft k2: Node(k2, Node(k1, X, Y), Z) -> Node(k1, X, Node(k2, Y, Z))
- 情况二:对左儿子的右子树进行一次插入(通过双旋转恢复平衡)
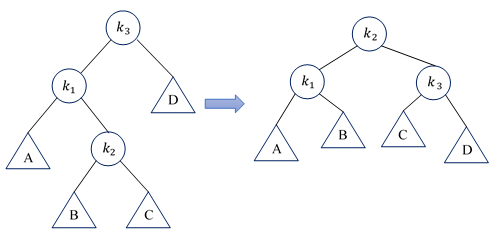
if k3左子树高度 - k3右子树高度 = 2 > 1 then
if k1左子树高度 - k1右子树高度 = -1 < 0 then
RotateRight k1: Node(k1, A, Node(k2, B, C)) -> Node(k2, Node(k1, A, B), C)
RotateLeft k3: Node(k3, Node(k2, Node(K1, A, B), C), D) -> Node(k2, Node(k1, A, B), Node(k3, C, D))
- 情况三:对右儿子的左子树进行一次插入 (和情况二镜像对称)
略 - 情况四:对右儿子的右子树进行一次插入 (和情况一镜像对称)
略
上面的情况一和情况二的if条件可以合并一下,同理适用于情况三和情况四,分析清楚后就有了下面的代码:
type ('k, 'v) avlnode =
| Leaf
| Node of int * 'k * 'v * ('k, 'v) avlnode * ('k, 'v) avlnode
let height (n : ('k, 'v) avlnode) : int =
match n with
| Leaf -> -1
| Node(h, _, _, _, _) -> h
let create k v l r =
Node(1 + max (height l) (height r), k, v, l, r)
let rotate_left n =
let k,v,l,r = get_elems n in
let lk,lv,ll,lr = get_elems l in
create lk lv ll (create k v lr r)
let rotate_right n =
let k,v,l,r = get_elems n in
let rk,rv,rl,rr = get_elems r in
create rk rv (create k v l rl) rr
let balance (n : ('k, 'v) avlnode) : ('k, 'v) avlnode =
let k,v,l,r = get_elems n in
if (height l)-(height r) > 1 then
let _, _, ll, lr = get_elems l in
rotate_left (
if (height ll)-(height lr) < 0 then
create k v (rotate_right l) r
else n
)
else if (height l)-(height r) < -1 then
let _, _, rl, rr = get_elems r in
rotate_right (
if (height rl)-(height rr) > 0 then
create k v l (rotate_left r)
else n
)
else n
let rec set (n : ('k, 'v) avlnode) (key : 'k) (value : 'v) : ('k, 'v) avlnode =
match n with
| Leaf -> create key value Leaf Leaf
| Node(_, k, v, l, r) ->
balance (
if k = key then create key value l r
else if key < k then create k v (set l key value) r
else create k v l (set r key value)
)
let add_all (n : ('k, 'v) avlnode) (keys : ('k * 'v) list) : ('k, 'v) avlnode =
List.fold_left (fun a (k, v) -> set a k v) n keys
2. 表达式求值
- 这里定义了一个算数类型,
例如表达式:
5 * 3 + y
可以表示为:
Plus(Times(Num(5), Num(3)), Variable("y"))
type arith =
| Plus of arith * arith
| Times of arith * arith
| Variable of string
| Num of int
- 实现了一个方法计算表达式的值,
例如执行:
evaluate (Times(Plus(Variable("x"), Variable("y")), Num(5))) (add_all Leaf [("x", 5); ("y", 7)])
会返回:
60
let rec evaluate (a : arith) (vars : (string, int) avlnode) : int =
let get_variable_value (key : string) (value : int option) : int =
match value with
| Some(num) -> num
| None -> failwith ("Variable " ^ key ^ " is not contained in vars in the expression")
in
match a with
| Plus(l, r) -> (evaluate l vars) + (evaluate r vars)
| Times(l, r) -> (evaluate l vars) * (evaluate r vars)
| Variable(var) -> get_variable_value var (get vars var)
| Num(num) -> num
- 实现一个方法把算数类型解析成数学表达式,
例如执行:
pretty (Plus(Plus(Times(Plus(Num(5), Variable("y")), Variable("x")), Num(2)), Num(1)))
会返回:
(5 + y)x + 2 + 1
let rec pretty (a : arith) : string =
let rec helper (a: arith) : string =
match a with
| Plus(_) -> "(" ^ pretty a ^ ")"
| _ -> pretty a
in
match a with
| Plus(l, r) -> pretty l ^ " + " ^ pretty r
| Times(l, r) -> helper l ^ helper r
| Variable(var) -> var
| Num(num) -> string_of_int num
3. 测试用例
- 省略了一些test case,仅演示用法
let t_any name value expected = name>::
(fun _ -> assert_equal expected value ~printer:dump);;
let a_tree = Node(0, "a", 5, Leaf, Leaf);;
let get_tests = [
t_any "get1" (get a_tree "a") (Some(5));
t_any "get2" (get (Node(0, "b", 15, a_tree, Leaf)) "a") (Some(5));
t_any "get3" (get (Node(0, "b", 15, a_tree, Leaf)) "c") None;
];;
let evaluate_tests = [
t_any "evaluate1" (evaluate (Times(Plus(Variable("x"), Variable("y")), Num(5))) (add_all Leaf [("x", 5); ("y", 7)])) 60;
];;
let pretty_tests = [
t_any "pretty1" (pretty (Plus(Plus(Times(Plus(Num(5), Variable("y")), Variable("x")), Num(2)), Num(1)))) "(5 + y)x + 2 + 1";
];;
let all_tests =
get_tests @
evaluate_tests @
pretty_tests
;;
let suite = "suite">:::all_tests;;
run_test_tt_main suite
- @函数的定义为:
val append : 'a list -> 'a list -> 'a list
Concatenate two lists. Same as the infix operator @. Not tail-recursive (length of the first argument).



