模式识别第二次作业
第二次作业
3.2
(a) K-means算法的任务是将数据集聚类成\(K\)个簇\(C=C_1,C_2,...,C_k\),使得所有数据到其所对应簇的距离最短,故其最小化损失函数为:
又根据\(\gamma_{i,j}\)定义且由\(\sum_{i=1}^{K}\gamma_{i,j}=1,\)变换损失函数:
(b) 当\(\mu_i\)固定时,由于每个样本只属于一个簇,所以找到距离样本\(j\)最近的簇的\(\mu_i\),令\(\gamma_{ij}=1\),其他的\(\gamma_{i,j}=0\),此时的距离和最小; 当\(\gamma_{ij}\)固定时,即每个样本所在的簇确定,\(\mu_i\)取所有\(y_{ij}\)为1时的平均值,即每个簇的中心,此时距离和取最小值。
(c) 证明:对于迭代的第一步,将每一个样本移到距离他最近的簇里面,根据书中式(5)可知\(\mu_i\)不变,该样本与簇中心距离减小,损失函数降低;对于迭代的第二步,将簇的中心变为该簇里面所有样本的中心,同样根据式(5),\(\gamma_{ij}\)不变,每个簇的损失函数都降低了。综上所述,由于迭代时损失函数在降低,因此一定会收敛。
4.2
(a) 优化问题,即最小化平方误差:
(b) \(\beta^*=\arg \min\limits_\beta (y-X\beta)^T(y-X\beta)\)
(c) 设代价函数为\(E\),对参数\(\beta\)求导并令其等于0得:\(\frac{\partial E}{\partial \beta}=-2X^T(y-X\beta)=0\)
假设\(X^TX\)可逆,则\(\beta = (X^TX)^{-1}X^Ty\)
(d) \(d>n\)时,即\(X\)的列数大于行数,变量维度大于样例数,由\(r(X^TX)=r(X)\),则\(X^TX\)不满秩,即不可逆。
(e) 正则项能防止过拟合,平衡方差和偏差,\(\lambda\)越大,模型方差越小,但偏差越大。同时保证了系数矩阵可逆,防止变量个数比样本数大的情况。
(f) \(\beta^*=\arg \min\limits_\beta (y-X\beta)^T(y-X\beta)+\lambda\beta^T\beta\)
\(\frac{\partial E^{'}}{\partial \beta}=-2X^T(y-X\beta)+2\lambda\beta=0\)得:
\(\beta = (X^TX+\lambda I)^{-1}X^Ty\)
(g) 岭回归在正则化之后保证了\((X^TX+\lambda I)\)满秩,解决了变量个数比样本数大的情况。
(h) \(\lambda=0\)时,岭回归与普通线性回归结果相同,即\(\beta = (X^TX)^{-1}X^Ty\),当\(\lambda=\infty\)时,\(\beta\simeq \frac{1}{\lambda}X^Ty\simeq0\),
(i)从训练集中多次选择一部分作为交叉验证集,每一次验证得到一个\(\lambda\)值及模型评分,选出评分最高的\(\lambda\)。
4.5
(a)AUR-PR和AP的计算:
| index | label | score | precision | recall | AUC-PR | AP |
|---|---|---|---|---|---|---|
| 0 | 1.0000 | 0.0000 | - | - | ||
| 1 | 1 | 1.0 | 1.0000 | 0.2000 | 0.2000 | 0.2000 |
| 2 | 2 | 0.9 | 0.5000 | 0.2000 | 0 | 0 |
| 3 | 1 | 0.8 | 0.6667 | 0.4000 | 0.1167 | 0.1333 |
| 4 | 1 | 0.7 | 0.7500 | 0.6000 | 0.1417 | 0.1500 |
| 5 | 2 | 0.6 | 0.6000 | 0.6000 | 0 | 0 |
| 6 | 1 | 0.5 | 0.6667 | 0.8000 | 0.1267 | 0.1333 |
| 7 | 2 | 0.4 | 0.5714 | 0.8000 | 0 | 0 |
| 8 | 2 | 0.3 | 0.5000 | 0.8000 | 0 | 0 |
| 9 | 1 | 0.2 | 0.5556 | 1.0000 | 0.1056 | 0.1111 |
| 10 | 2 | 0.1 | 0.5000 | 1.0000 | 0 | 0 |
| 0.6907 | 0.7277 |
(b) 由表可知,AUC-PR和AP的值相差不大,每一项差在0.01以内,最终差0.07。
(c) 交换数据后,后两行:
| index | label | score | precision | recall | AUC-PR | AP |
|---|---|---|---|---|---|---|
| 9 | 2 | 0.2 | 0.4444 | 0.8000 | 0 | 0 |
| 10 | 1 | 0.1 | 0.5000 | 1.0000 | 0.0944 | 0.1 |
| 0.6795 | 0.7166 |
对数据顺序较敏感。
(d) 代码:
function cal(data)
sum_PR = 0 ; sum_AP = 0; %输出
P=1;R=0;TP =0;
sum1=0; #样本为1的个数
for i=1:size(data,1)
if(data(i,1)==1)
sum1+=1;
endif
end
%按照第二列得分进行排序
data0 = flipud(sortrows(data,2));
for i=1:size(data,1)
if(data0(i,1)==1)
TP +=1;
endif
PR = (TP/sum1-R)*(P+TP/i)/2;
AP = (TP/sum1-R)*TP/i;
R = TP/sum1;
P= TP/i;
sum_PR+=PR;
sum_AP+=AP;
endfor
sum_PR
sum_AP
endfunction
实验结果:
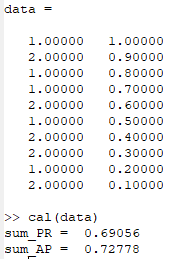
与手算结果基本一样。
4.6
(a) \(E\left [ (y-f(x,D))^2 \right ]=(F(x)-E_D[f(x;D)])^2+E_D[(f(x;D)-E_D[f(x;D)])^2]+\sigma^2\)
其中第一项是偏置的平方,第二项是方差,第三项是噪声。
(b)
(c)
(d) 方差:
由上式可知,方差降低到了\(\frac{1}{k}\),因此\(k\)越大,方差越小。
(e) 偏置的平方:\((F(x)-\frac{1}{k}\sum_{i=1}^{k}F(x_{nn(i)}))^2\)
随着k的减小,由于是\(k\)个与\(x\)最近的样本,\(\frac{1}{k}\sum_{i=1}^{k}F(x_{nn(i)})\)与\(F(x)\)越接近,即偏置平方越小,\(k=n\)时即为所有样本平均值。
综上所述,\(k\)对偏置和方差影响相反。
5.5
(a) 证明:设\(G=(g_1,g_2,...,g_n)\),列向量长度为1且相互正交,
即正交变换不改变向量长度。
(b) 证明:已知定理:\(tr(AB)=tr(BA)\)
(c) 求\(X\)的特征向量和特征值即找到一个正交矩阵\(P\)使得\(P^TXP=PD\),其中D为对角矩阵,其对角线元素为\(X\)的特征值,P的列向量为\(X\)的特征值。如果能找到正交矩阵\(J\)使得:\(off(J^TXJ)<off(X)\),不难看出做一次变换之后新矩阵的对角线之外的元素平方减小了,因此我们可以不断迭代这个过程,直到非对角元素平方和全为0,即非对角元素全为0,此时得到的对角矩阵元素即为特征值,而由于正交矩阵相乘仍然是正交矩阵,即得到\(P\),即:
(d) 构造一个高维的旋转矩阵:
\(J(i,i,\theta)[p][p]=J(j,j,\theta)[q][q]=\cos\theta\),\(J(i,j,\theta)[p][q]=-\sin\theta\) ,\(J(p,q,\theta)[j][i]=\sin\theta\),对角线其余元素都为1,非对角线其余元素都为0.
设做一次Givens旋转变换得到\(X^{'}\):\(X^{'}=J^TXJ\),即:
令其等于0得:\(\theta = \frac{1}{2}\arctan\frac{2X_{i,j}}{X_{i,i}-X_{j,j}}\),则\(J^TXJ\)中\((i,j)\)项和\((j,i)\)项都变成0。
(e) 上面分析了\((p,q)\)和\((q,p)\)位置的元素,考虑其他非对角元素:
注意以上等式的条件为$i\neq p,q \(,\)j\neq p,q$,将上述四个式子两边平方再相加:
\(X^{'2}_{p,i}+X^{'2}_{q,i}+X^{'2}_{j,p}+X^{'2}_{j,q}=(X_{q,i}^2+X_{q,i}^2+X_{j,q}^2+X_{j,q}^2)\)
而其余的非对角元素为0,因此只有\((p,q)\)和\((q,p)\)位置的元素变为0,\(off(X)\)减少了\(2X_{i,j}^2\),故一次迭代不会增加\(off(X)\)。
(f) 由(e)只,每次迭代都能使一对非对角元素变为0(\(off(X)\)减少了\(2X_{i,j}^2\)),因此不断迭代该过程,最终能使\(off(x)=0\),因此该算法收敛。

