坐标变换

坐标变换在机器人领域十分常见，推导了几种从易到难的坐标转换：

1.二维平面绕原点旋转

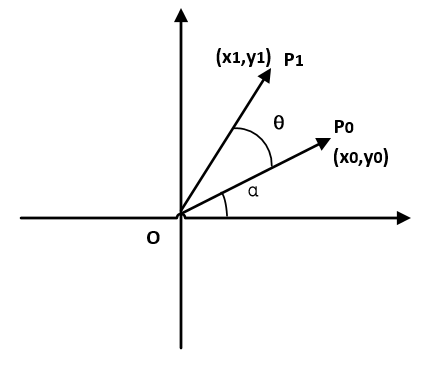
 如图所示，O为原点，旋转角为$\theta$，P0、P1坐标分别为$(x_0,y_0)、(x_1,y_1)$，P0与X轴夹角为$\alpha$，设P0和P1到原点距离为$r$，则P0坐标为：

\begin{equation}
\left\{
\begin{array}{lr}
x_0 = r\cos\alpha \\
y_0 = r\sin\alpha 
\end{array}
\right.
\end{equation}

P1坐标为：

\begin{equation}
\left\{
\begin{array}{lr}
x_1 = r\cos(\alpha+\theta) = r\cos\theta\cos\alpha-r\sin\theta\sin\alpha \\
y_1 = r\sin(\alpha+\theta) = r\sin\theta\sin\alpha+r\cos\theta\sin\alpha
\end{array}
\right.
\end{equation}

 将公式(1)带入到公式2,，消去$r$得

\begin{equation}
\left\{
\begin{array}{lr}
x_1 = x_0\cos\theta-y_0\sin\theta \\
y_1 = x_0\sin\theta+y_0\cos\theta
\end{array}
\right.
\end{equation}

式(3)为由P0逆时针旋转至P1的表达式，也可通过该式求出由P1到P0的变换：

\begin{equation}
\left\{
\begin{array}{lr}
x_0 = -x_1\sin\theta+y_1\cos\theta \\
y_0 = x_1\cos\theta+y_1\sin\theta
\end{array}
\right.
\end{equation}

也可以用矩阵来表示变换,逆时针旋转$\theta$：

\begin{equation}
\left[
\begin{array}{lr}
x_1\\
y_1
\end{array}
\right ]
=
\left[
\begin{array}{lr}
cos\theta&-sin\theta \\
sin\theta&cos\theta
\end{array}
\right ]
\left[
\begin{array}{lr}
x_0\\
y_0
\end{array}
\right ]
\end{equation}

顺时针旋转$\theta$：

\begin{equation}
\left[
\begin{array}{lr}
x_0\\
y_0
\end{array}
\right ]
=
\left[
\begin{array}{lr}
-sin\theta&cos\theta \\
cos\theta&sin\theta
\end{array}
\right ]
\left[
\begin{array}{lr}
x_1\\
y_1
\end{array}
\right ]
\end{equation}

 二者的系数矩阵相互可逆。

2.二维平面绕固定点旋转

 

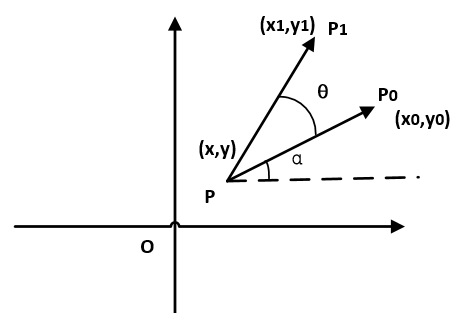
 如上图所示，现在改为绕P点旋转，点到P的距离为$r$。推导的方法和1中一致，设P0与x轴正方向夹角为$\alpha$。则P0坐标为：

\begin{equation}
\left\{
\begin{array}{lr}
x_0 = r\cos\alpha+x \\
y_0 = r\sin\alpha+y 
\end{array}
\right.
\end{equation}

P1坐标为：

\begin{equation}
\left\{
\begin{array}{lr}
x_1 = r\cos(\alpha+\theta) +x = r\cos\theta\cos\alpha-r\sin\theta\sin\alpha+x \\
y_1 = r\sin(\alpha+\theta) +x = r\sin\theta\sin\alpha+r\cos\theta\sin\alpha+y
\end{array}
\right.
\end{equation}

将(7)式代入(8)式，消去$r$得：

\begin{equation}
\left\{
\begin{array}{lr}
x_1 = (x_0-x)\cos\theta-(y_0-y)\sin\theta +x\\
y_1 = (x_0-x)\sin\theta+(y_0-y)\cos\theta +y
\end{array}
\right.
\end{equation}

同理也可以由式(9)得到$x_0$、$y_0$的表达式

\begin{equation}
\left\{
\begin{array}{lr}
x_0 =-(x_1-x)\sin\theta+(y_1-y)\cos\theta+x \\
y_0 = (x_1-x)\cos\theta+(y_1-y)\sin\theta+y
\end{array}
\right.
\end{equation}

使用矩阵来表示，逆时针旋转$\theta$：

\begin{equation}
\left[
\begin{array}{lr}
x_1\\
y_1
\end{array}
\right ]
=
\left[
\begin{array}{lr}
cos\theta&-sin\theta \\
sin\theta&cos\theta
\end{array}
\right ]
\left[
\begin{array}{lr}
x_0-x\\
y_0-y
\end{array}
\right ]
+
\left[
\begin{array}{lr}
x\\
y
\end{array}
\right ]
\end{equation}

顺时针旋转$\theta$：

\begin{equation}
\left[
\begin{array}{lr}
x_0\\
y_0
\end{array}
\right ]
=
\left[
\begin{array}{lr}
-sin\theta&cos\theta \\
cos\theta&sin\theta
\end{array}
\right ]
\left[
\begin{array}{lr}
x_1-x\\
y_1-y
\end{array}
\right ]
+
\left[
\begin{array}{lr}
x\\
y
\end{array}
\right ]
\end{equation}