论文阅读：hector_slam: A Flexible and Scalable SLAM System with Full 3D Motion Estimation.

参考：《A Flexible and Scalable SLAM System with Full 3D Motion Estimation.》

该论文是ROS中hector_mapping建图包的论文，发表于2010年但hector_mapping在ROS中只更新到了Kinetic版本。毕设轮椅导航用到了这个导航，拿出来读了一下，二维部分还是很好懂的，公式也比较简单。

已经有人翻译过了这篇文章：https://www.cnblogs.com/cyberniklee/p/8484104.html

之前不知道为什么叫hector_slam，因为提出该方法的团队叫Heterogeneous Cooperating Team Of Robots（异构机器人协作团队），团队官网：http://www.teamhector.de/

该算法已经在ROS中开源：http://wiki.ros.org/hector_slam

论文中提出了一种快速在线学习占用栅格地图，占用较少计算资源的系统。结合了激光雷达与惯性传感器进行融合，采用了多分辨率栅格地图解决梯度方法带来的局部最小问题。本文的方法只提供了SLAM中的前端部分，不提供位姿优化，没有闭环检测。因此该方法有时无法建立闭环的地图。主要利用了雷达的高速扫描速率。

目前只读了二维SLAM部分：

首先对于扫描的三维数据点可以先进行预处理（三维点应该要先转换为二维点），如降采样或者移除无效点，文中采用了基于Z坐标的滤波，只保留了需要平面的点，即根据Z值设置一个阈值，保留阈值高度内的点。

占用栅格地图

占用栅格地图是离散的，因此会限制精度，且不能计算插值或导数，因此对于每个激光点，利用周围四个网格点对其进行双线性插值。即网格映射单元格值可以看作是底层连续概率分布的样本。

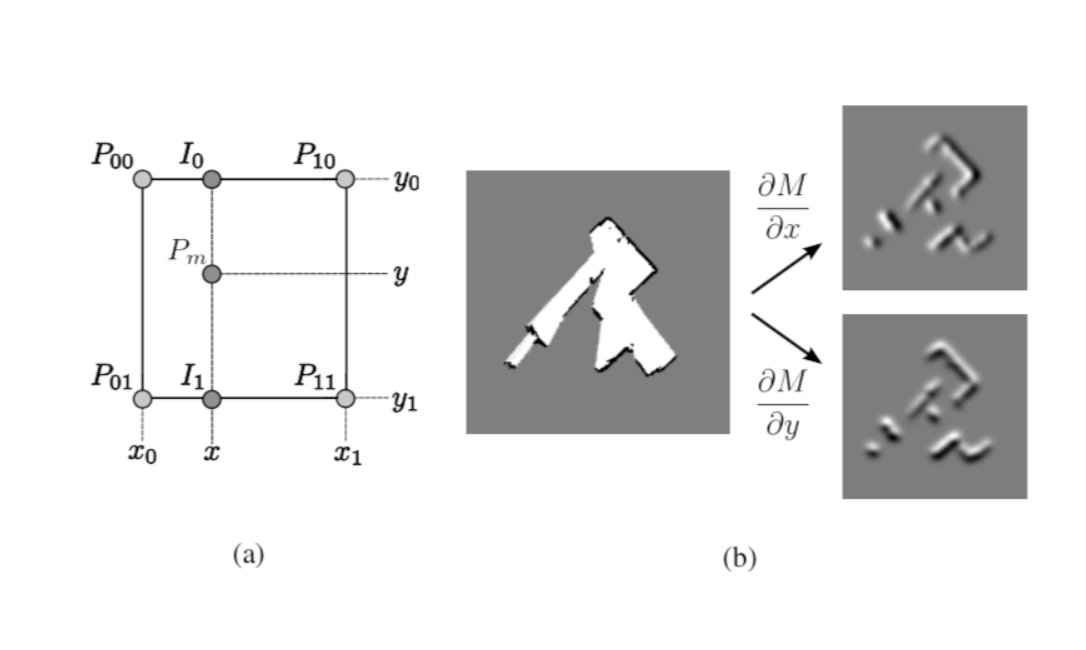
 对于连续的地图坐标$P(m)$，使用占用值$M(P_m)$表示该点被映射为占据点的概率，其梯度为$\bigtriangledown M(P_m)=(\frac{\partial_M}{\partial_x}(P_m),\frac{\partial_M}{\partial_y}(P_m))$,$M(P_m)$使用上图a中的四个点$P_{00}$、$P_{10}$、$P_{01}$、$P_{11}$分别在x轴和y轴进行线性插值后求得：（关于线性插值）

$P_{00}$、$P_{10}$在x轴上进行插值得到$I_0$：

$$M(I_0)= \frac{x-x_0}{x_1-x_0}M(P_{10})+\frac{x_1-x}{x_1-x_0}M(P_{00})\tag{1}$$

$P_{01}$、$P_{11}$在x轴上进行插值得到$I_1$：

$$M(I_1)= \frac{x-x_0}{x_1-x_0}M(P_{11})+\frac{x_1-x}{x_1-x_0}M(P_{01})\tag{2}$$

对$I_0$和$I_1$在y轴上进行线性插值得到$P_m$

$$M(P_m)= \frac{y-y_0}{y_1-y_0}M(I_1)+\frac{y_1-y}{y_1-y_0}M(I_0)\tag{3}$$

即：

$$M(P_m)= \frac{y-y_0}{y_1-y_0} (\frac{x-x_0}{x_1-x_0}M(P_{11})+\frac{x_1-x}{x_1-x_0}M(P_{01}))+\frac{y_1-y}{y_1-y_0}(\frac{x-x_0}{x_1-x_0}M(P_{11})+\frac{x_1-x}{x_1-x_0}M(P_{01}))\tag{4}$$

由于插值的四个点处于一个网格，单位距离为1，可认为$x_1-x_0=1$、$y_1-y_0=1$，因此导数可近似为：

$$\frac{\partial_M}{\partial_x}(P_m)=\frac{y-y_0}{y_1-y_0}(M(P_{11})-M(P_{01}))+\frac{y_1-y}{y_1-y_0}(M(P_{10})-M(P_{00}))\tag{5}$$

$$\frac{\partial_M}{\partial_x}(P_m)=\frac{y-y_0}{y_1-y_0}(M(P_{11})-M(P_{01}))+\frac{y_1-y}{y_1-y_0}(M(P_{10})-M(P_{00}))\tag{6}$$

扫描匹配

扫描匹配即是将激光雷达扫描与现有地图对齐的过程，由于目前激光扫描的精度很高、扫描速度快，比里程计精度高很多，因此未使用里程计数据。

论文中的方法是基于已知地图的端点对齐优化方法。基本方法为高斯-牛顿法，不需要再激光端点之间进行数据关联搜索或穷举搜索。

将获取的激光数据作为第一帧。在$t$时刻，激光扫描数据要与$t-1$时刻的地图匹配，激光点应尽可能得映射到占据栅格中，如果所有的激光点都能映射到占据栅格中，则说明前后帧匹配成功。上一节中$M(P_m)$表示点$P_m$映射到占据栅格的概率，取值范围为0-1双线性插值方法求出。

对于每一个激光点，希望$M(P_m)$尽可能大，因此构造目标函数：
$$\varepsilon ^* = \mathop{argmin}\limits_{\varepsilon }\sum_{i=1}^{n}{[1-M(S_i(\varepsilon))]^2}\tag{7}$$

其中$\varepsilon=(P_x,P_y,\phi)$为为机器人位于地图中的位姿，$S_i(\varepsilon)$为在第$t$时刻将第i个激光点映射到地图坐标系下，在建立地图坐标时需要注意各坐标系之间的转换关系。选择地图为全局坐标系，轮椅相对于地图的位姿为$\varepsilon$，而激光端点相对于轮椅其坐标为$s_i=(s_{i,x},s_{i,y})$。因此需要将激光数据转换到全局坐标系（地图），即做一个旋转平移变换：

$$
S_i(\varepsilon)
=
\left[
\begin{array}{lr}
cos(\phi)&-sin(\phi) \\
sin(\phi)&cos(\phi)
\end{array}
\right ]
\left[
\begin{array}{lr}
s_{i,x}\\
s_{i,y}
\end{array}
\right ]
+
\left[
\begin{array}{lr}
p_x\\
p_y
\end{array}
\right ]
\tag{8}$$

 $M(S_i(\varepsilon))$返回坐标$S_i(\varepsilon)$的地图值，对于某个起始的位姿$\varepsilon$，我们希望估计出$\Delta \varepsilon$，通过以下方程优化测量误差：

$$\sum_{i=1}^n[1-M(S_i(\varepsilon+\Delta\varepsilon))]^2\rightarrow 0\tag{9}$$

对于$M(S_i(\varepsilon+\Delta\varepsilon))$在$\varepsilon$处进行一阶泰勒展开：

$$\sum_{i=1}^n[1-M(S_i(\varepsilon))-\nabla M(S_i(\varepsilon))\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}\Delta\varepsilon]^2\rightarrow 0\tag{10}$$

 为了得到整张地图，需要知道上一帧的地图和当前的位姿增量，因此式(10)对$\Delta\varepsilon$求导得：

$$2\sum_{i=1}^n[\nabla M(S_i(\varepsilon))\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}]^T[1-M(S_i(\varepsilon))-\nabla M(S_i(\varepsilon))\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}\Delta\varepsilon]\rightarrow 0\tag{11}$$

根据式(11)可求出$\Delta \varepsilon$：

$$\Delta \varepsilon = H^{-1}\sum_{i=1}^n[\nabla M(S_i(\varepsilon))\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}]^T[1-M(S_i(\varepsilon))]\tag{12}$$

 其中：

$$H=[\nabla M(S_i(\varepsilon))\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}]^T[\nabla M(S_i(\varepsilon))\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}]\tag{13}$$

$\nabla M(S_i(\varepsilon))$可以直接通过占用栅格地图部分的偏导公式求出，根据公式(8)及$\varepsilon=(P_x,P_y,\phi)$可得：

$$
\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}
=
\left[
\begin{array}{lr}
1&0&-sin(\phi)s_{i,x}-cos(\phi)s_{i,y} \\
0&1&cos(\phi)s_{i,x}-sin(\phi)s_{i,y}
\end{array}
\right ]
\tag{14}$$

根据$\nabla M(S_i(\varepsilon))$和$\frac{\partial S_i(\varepsilon)}{\partial \varepsilon}$可以求出式12中的$\varepsilon$，且接近于最小值，$\varepsilon$即为位姿变化，根据已知地图和当前数据帧之间的位姿增量，能获取建图时位置，并将新的数据帧更新到地图中，该算法适用于非光滑线性逼近的地图梯度$\nabla M(S_i(\varepsilon))$，这意味着不能保证局部二次收敛到最小，但该算法在实践中精度较高。

多分辨率地图

梯度法有陷入局部最小的风险，使用计算机视觉中类似于图像金字塔方法在多分辨率地图中可以缓解该问题。论文中选择多个占用栅格地图，每个粗糙的地图为上一层地图分辨率的一半。低分辨率地图不是由高分辨率地图直接得到，而是进行同步更新，避免了降采样操作。扫描定位时从低分辨率地图开始，估计的位姿作为下一级地图的开始进行估计。其优点为低分辨率地图随时可以使用于路径规划等。

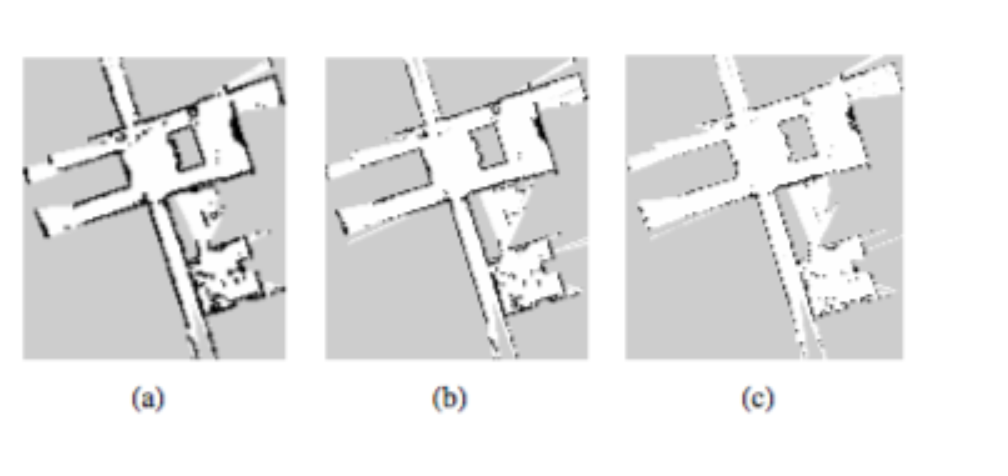
如上图所示，分辨率依次降低。

 

总结：hector_slam利用了激光雷达的高速扫描频率，没有闭环检测，但在机器人快速转弯时容易发生错误，原因在于优化算法容易陷入局部最小值。在ROS中使用hector算法建了一张地图，精度挺高的，但是不能闭环，有点偏差，建图时机器人速度已经很慢了。

 

 

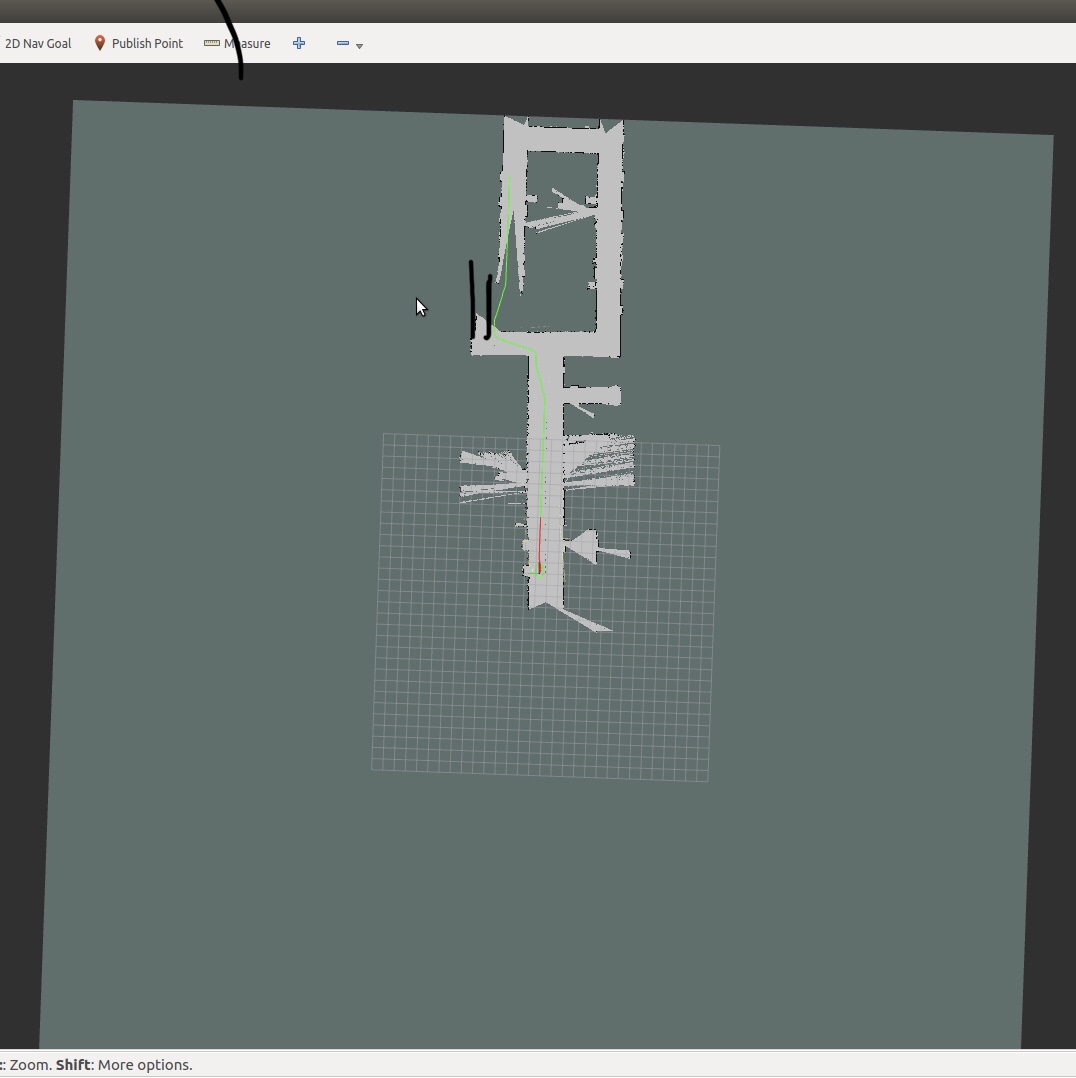
 三维hector_slam还没有用过，以后再读。。。