模拟退火算法的理论基础
模拟退火算法是一种基于概率的,可以有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。通常用于解决:可行解过多、传统算法运算时间过长、筹款组合方案过多和NP-hard等问题
一、模拟退火的思想与提出
1.基本思想
模拟退火的基本思想,就是走出舒适圈,多去“试一试”,万一成了呢?这里的试一试,就是通过基于概率地试探新解,从而跳出局部最优
舒适区:当前处于局部最优解
试一试:随机试探新解,有更好的解就直接选新解,没更好的则以一定概率选择新解
万一成了:找到了更优解甚至最优解
2.贪心算法失效--陷入局部最优
从爬山说起,假如登高者想要在日落前爬上一座山的最高峰(求最优解)。
但山中云雾缭绕、视野受限,只能看到当前位置附近一定范围内的情况贪心算法:在视野内选取一个点,如果更高,就过去;否则就不去直到视野内没有更高的点,则输出当前解作为最终解。
显然,这种情况很容易出现:当登高者走到某个小山峰时,四周看不到更高的点,就不会走下山去、寻找更高的峰。从而陷入了局部最优解
3.模拟退火如何解决解决陷入局部最优?
那么在可见范围内,随机选择一点
(1)如果该点比当前位置更高,就直接去该点(优化)
(2)如果该点更低,那么就多掷几次硬币,结合该点与当前点的高度差决定去不去(一定概率在刚才的局部最优解的峰,会有一定概率走下了当前山峰,从而发现另一个山峰的上坡。从而就有可能走上新的更高峰)
二、模拟退火算法解决TSP问题
1.问题提出

2.问题分析
若把所有可能的路线方案都列出来再求最小值,则有33!(33的阶乘)种方案,这是10^36数量级,无论是使用蒙特卡洛模拟还是遍历计算,运算时间会很长。
此时可考虑使用模拟退火
3.模型建立
(1)符号建立
题目要求以北京作为起点和终点,那么设起点北京为1号城市x1。余下需要遍历的33个城市依次设为x2,x3.....,x34
最后还需回到北京,设终点北京为35号城市X35
(2)设立目标函数

三、模拟退火算法的求解步骤
1.初始化变量
设定一个初始温度T和问题的一个初始解x(0)
有那么多种可行解,可以随便选一个作为初始解。例如本题,可以把原始数据的排列直接作为初始解,解为x1x2x3…x35。
2.随机产生新解
在当前温度T下随机求一个解X',制定产生新解的准则(准则不唯一,能确保随机即可)。
假设上一步的解为:
X1...Xu-1 Xu Xu+1...Xv-1 Xv Xv+1...X35
随机选序号u,v,将u到v的这部分转为逆序,得到解:
X1...Xu-1 Xv Xv-1...Xu+1 Xu Xv+1...X35
3.计算目标函数差值
我们把解依次分成三部分,第一部分和第三部分是没有被改变的解,因此他们的差值是0。而第二部分只是顺序改变,因此他们的差值仍然是0。因此变化的仅仅是第一部分与第二部分与第二部分与第三部分的相接处,因此可以得到他们的差值Δf
随机得到的解X'和当前解X(i),两种方案总路径的差值记为Δf。
Δf =(dXu-1Xv+dXuXv+1)-(dXu-1Xu+dXvXv+1)
4.是否接受新解
我们之前已经说明过,模拟退火算法是基于概率的优化算法,下方是我们的接受新解的概率。
当Δf<0,肯定接受,因为比之前更好;Δf>0,我们也以一定的概率接受。如果Δf的值较小,接受的概率高。T大,接受的概率高
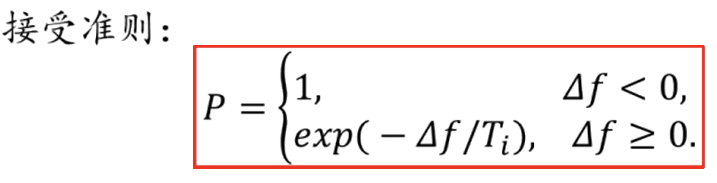
5.马尔科夫过程
在当前温度Ti下,重复2、3、4步
温度Ti不变时,判断准则中的exp(-Δf/Ti)由f决定,而f由随机解X'和当前解X(i)决定。所以新解X(i+1)只与X(i)有关,而与更早的X(i-1),X(i-2),…….x(0)无关。
显然这是个马尔科夫过程,x在原解x(i)的邻域中符合均匀分布
6.退火过程
选定降温系数a,求得新温度Ti+1=a*Ti,此处设为0.999
再重复2、3、4、5步;然后继续降低温度....
7.结束条件
直到温度足够小,设终止温度为e=10e-30,当T<e时终止迭代,输出最终解。
退火过程足够慢、每个温度下寻找新解的次数足够多,则最终解是全局最优解的概率越大
四、为什么模拟退火算法在理论上能找到最优解?
1.玻尔兹曼分布
温度Ti下解的平衡态X满足玻尔兹曼分布:

2.状态转移概率

3.当Δf趋于0时,玻尔兹曼分布才存在
玻尔兹曼分布可知,当Ti确定时,该式的分母是确定的,把它看作一个常数。
我们把目光放在我们的分子上,温度T→0时,指数项趋于负无穷,分子趋于0,那么分布不存在。也就意味着只有f(xi)尽可能趋于0的状态才会存在。对应现实问题,求得的最终解中只有fmin,也就是最优解
4.当Δf趋于0时,即找到了最优解,状态转移概率趋于0
从状态转移概率公式可知,当温度T→0,Δf>0时转移到更高函数值的概率趋近于0也就意味着温度极低时,转移到更差解的概率越小、会以更大概率停留在当前解
5.结论
结论:当寻找新解次数足够多、降低温度足够慢,最终会以接近于1的概率求得全局最优解
6.理论上模拟退火找到最优解的概率为 1/最优解的个数
这里的abs(S_min)为最优解的个数



