粒子群算法中对于学习因子的改进
个体学习因子c1和社会(群体)学习因子c2决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响，其反映了粒子群之间的信息交流。设置c1较大的值，会使粒子过多地在自身的局部范围内搜索，而较大的c2的值，则又会促使粒子过早收敛到局部最优值。那么如何改进这两个因子的取值才能更好地找到我们的最优解呢？下面我们来介绍两个方法
一、压缩因子法
为了有效地控制粒子的飞行速度，使算法达到全局搜索与局部搜索两者间的有效平衡，Clerc构造了引入收缩因子的PS0模型，采用了压缩因子，这种调整方法通过合适选取参数，可确保PS0算法的收敛性，并可取消对速度的边界限制
1.算法公式
引入压缩因子后，我们只需要在迭代速度之前乘上压缩因子即可。这样会使我们速度变小，从而控制飞行速度，加入这个限制之后，我们也可以在循环中取消对速度是否超出边界的的判断，加快了运行速度
2.代码实现
fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子
v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)));
二、非对称学习因子
在经典PSO算法中，由于在寻优后期粒子缺乏多样性，易过早收敛于局部极值，因此通过调节学习因子，在搜索初期使粒子进行大范围搜索，以期获得具有更好多样性的高质量粒子，尽可能摆脱局部极值的干扰。
1.算法思想
搜索的初期，我们希望广撒网，也就是尽量使粒子遍历全局解空间，进行全局搜索。c1的值变大会导致粒子在自身的局部最优解周围进行搜索，使粒子尽量发散到搜索空间，即强调“个体独立意识”，有利于全局搜索。
相反，c2越大的话，局部的搜索能力就越强。
因此在初期，我们个体学习因子c1的值应该增大，c2的值变小，有利于全局搜索；在后期减少c1的值，增大c2的值，有利于局部搜索进行收敛。
2.算法公式
随着迭代次数的增加，使c1线性递减，c2线性递增，从而加强了粒子向全局最优点的收敛能力
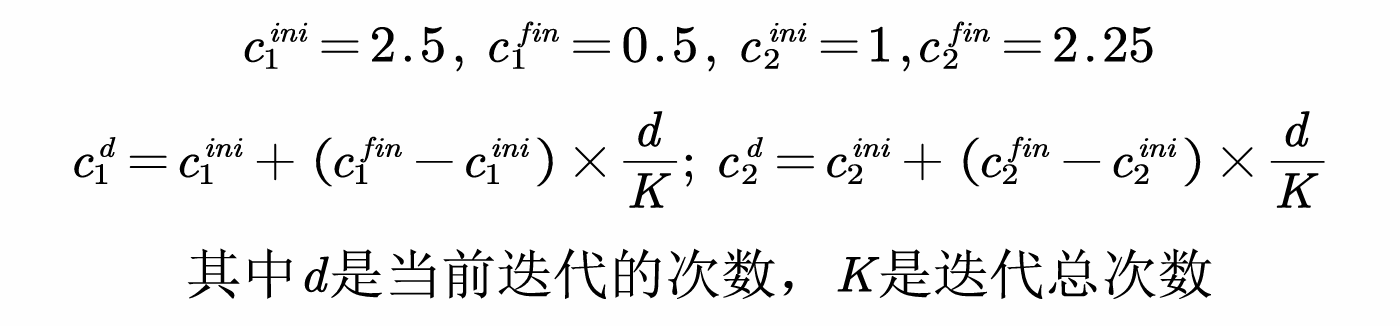
3.代码实现
同样，在迭代速度之前迭代c1与c2
for d = 1:K % 开始迭代，一共迭代K次
% w = 0.9 - 0.5*d/K; % 效果不是很好的话可以同时考虑线性递减权重
c1 = c1_ini + (c1_fin - c1_ini)*d/K;
c2 = c2_ini + (c2_fin - c2_ini)*d/K;
for i = 1:n % 依次更新第i个粒子的速度与位置
v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度
