粒子群算法初步与在求函数最值上的应用
粒子群算法是一种优化算法,也是一种启发式算法。按照预定的策略实行搜索,在搜索过程中获取的中间信息不用来改进策略,称为盲目搜索;反之,如果利用了中间信息来改进搜索策略则称为启发式搜索。
蒙特卡罗模拟用来求解优化问题就是盲目搜索,还有大家熟悉的枚举法也是盲目搜索。因为其并没有利用到中间获得到的信息
启发式算法(heuristic algorithm)是相对于最优化算法提出的,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解
一、粒子群算法的直观解释
它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。
鸟群觅食的过程完美地体现了这一思想,我们来介绍一下
设想这样一个场景:一群鸟在搜索食物
1.基础假设
(1)所有的鸟都不知道食物在哪
(2)它们知道自己的当前位置距离食物有多远
(3)它们知道离食物最近的鸟的位置
2.鸟的行动轨迹
(1)鸟的行动轨迹受其他鸟的影响
首先,离食物最近的鸟会对其他的鸟说:兄弟们,你们快往我这个方向来,我这离食物最近。因此,其他鸟有向这只鸟移动的趋势
(2)鸟的行动轨迹受自我经历的影响
与此同时,每只鸟在搜索食物的过程中,它们的位置也在不停变化,因此每只鸟也知道自己离食物最近的位置,这也是它们的一个参考;因此,每只鸟有自己的思想,有向自己想要去的方向移动的趋势
(3)鸟的行动轨迹受惯性的影响
在物理学上,惯性是物体保持静止状态或匀速直线运动状态的性质。在这里,惯性的作用则体现在鸟在一定程度上保持自己原本的方向运动
3.个体行动轨迹的模型建立
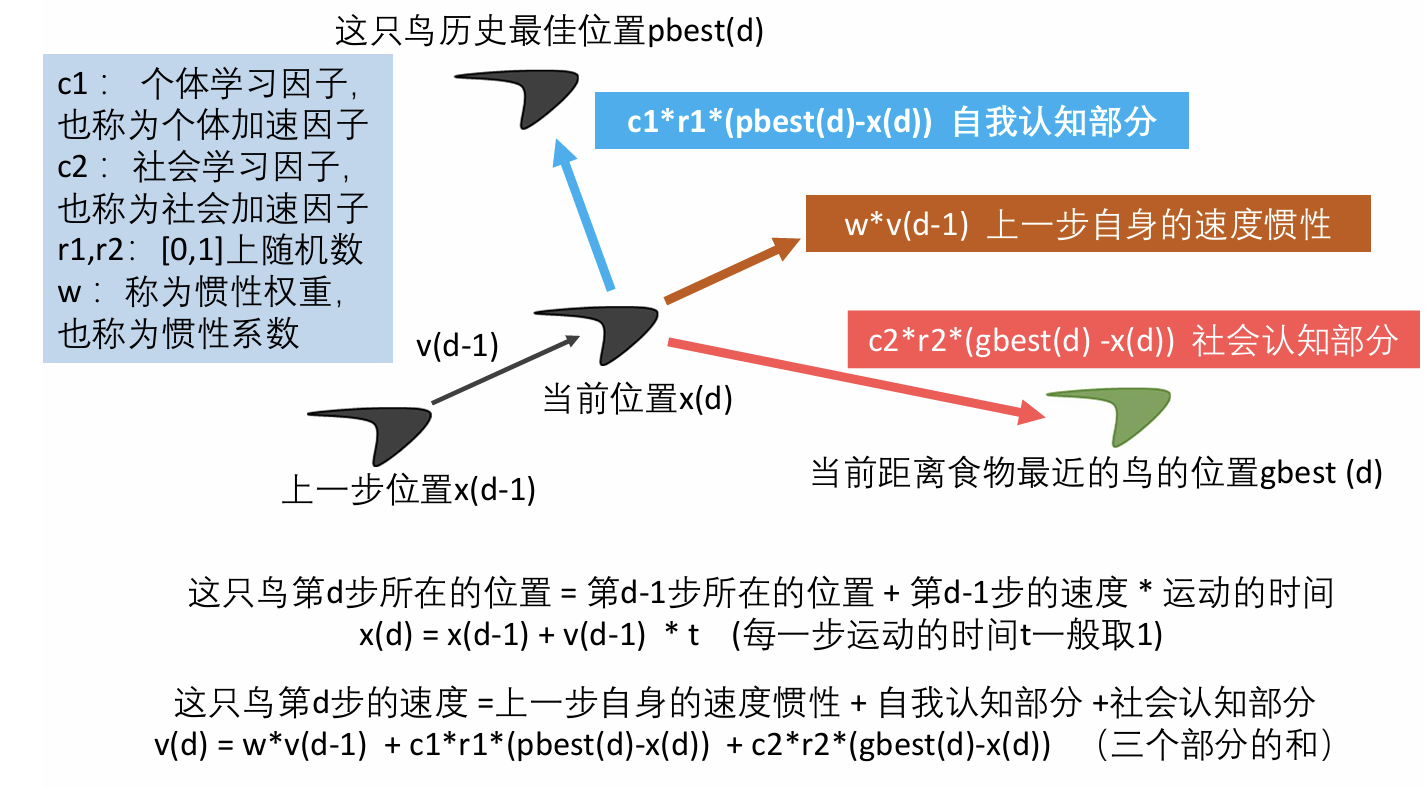
我们已经知道,鸟的行动受到三个部分的影响。受到其他鸟的影响我们称为社会学习因子;受到自我经历的影响我们称为个体学习因子;受惯性的影响我们称为惯性权重。
因此鸟的速度就由三个部分组成,因此,这只鸟第d步的速度=上一步自身的速度惯性+自我认知部分+社会认知部分
而位置则由上一步的位置加上速度,因为这里的我们运用的是一步一步进行计算,因此t=1
4.小结
通过鸟群的信息共享,鸟群可以更快地找到食物,而我们也需要运用这样信息共享的思想,进行一步一步地迭代,找到我们优化问题的解
二、粒子群算法中的名词解释
粒子:优化问题的候选解;在鸟群中相当于鸟的个数,粒子越多,鸟越多,能找到食物的概率也就越大。但是过多的粒子数会造成运算速度变慢。在我们今天的问题中就是x
位置:候选解所在的位置
速度:候选解移动的速度
适应度:评价粒子优劣的值,一般设置为目标函数值
个体最佳位置:单个粒子迄今为止找到的最佳位置;有n(n为粒子的个数)个值
群体最佳位置:所有粒子迄今为止找到的最佳位置;只有1个值,这个值是上面n个值的最优值
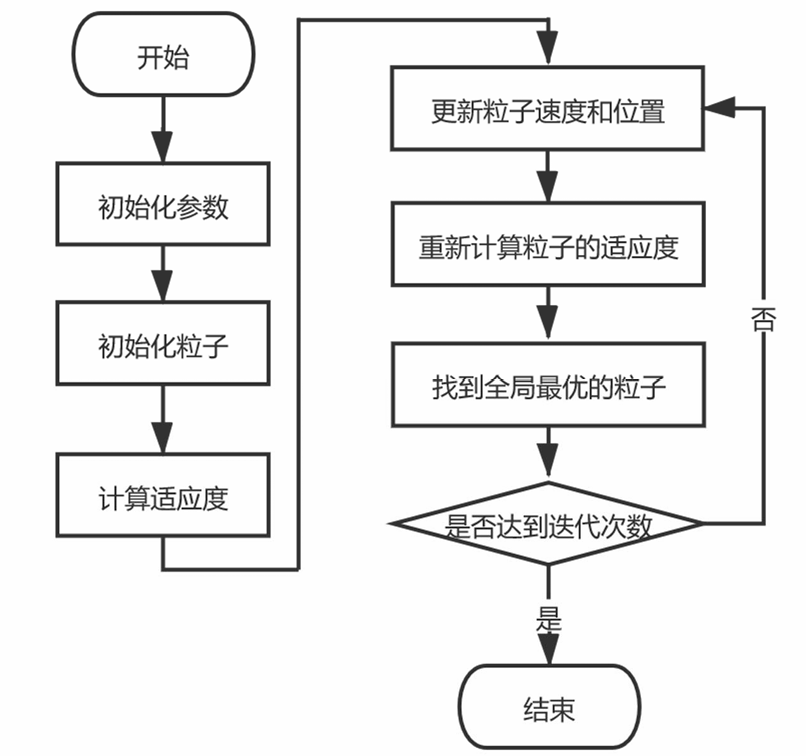
三、粒子群算法流程图
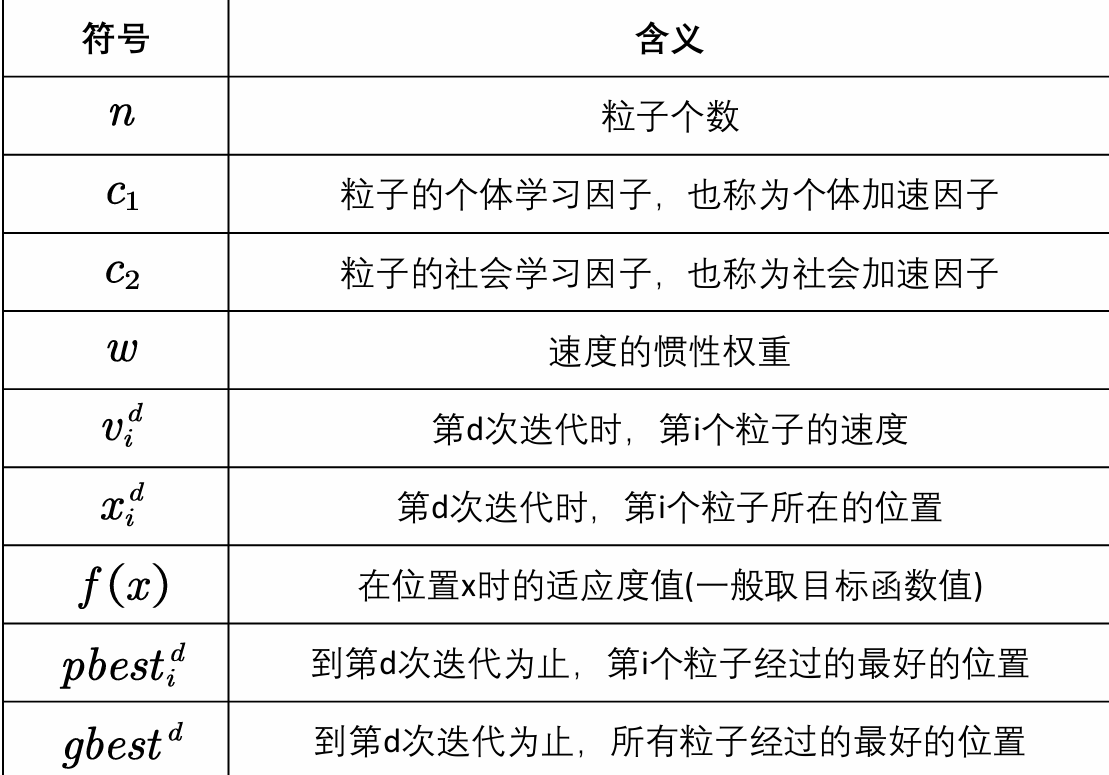
四、符号说明
五、粒子群算法的核心公式

1.预设参数:学习因子

2.预设参数:惯性权重

六、用matlab求一元函数的最大值
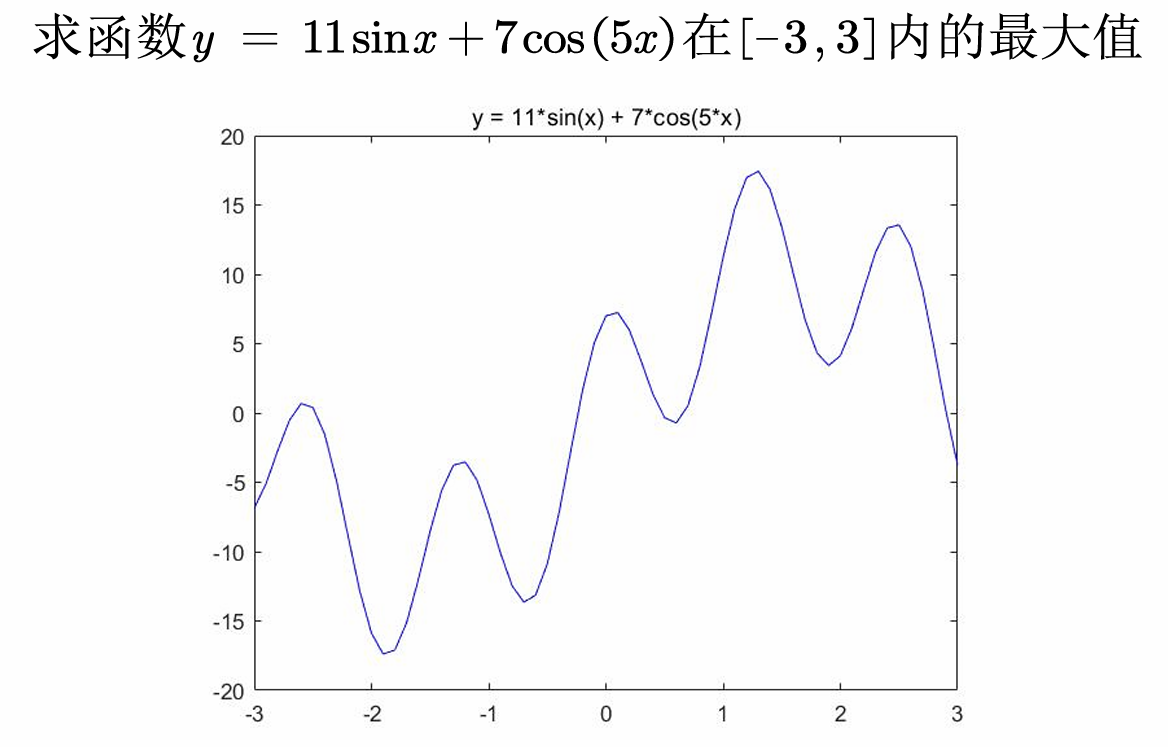
1.尝试使用fmincon求解非线性函数
我们在之前的规划模型中介绍了fmincon函数求解非线性函数,但是这个函数对初值的要求非常高,在复杂的函数问题下,我们很难得到一个合适的初值从而得到一个合适的解
由函数图像可以看到,最大值在[1,1.5]可以取到,下面我们尝试用不同的初值来尝试求解
x0 = 0;x1=2;
[x_0,fval_0] = fmincon(@Obj_fun1,x0,A,b,Aeq,beq,x_lb,x_ub);
[x_1,fval_1] = fmincon(@Obj_fun1,x1,A,b,Aeq,beq,x_lb,x_ub);
fval_0 = -fval_0;fval_1 = -fval_1;
% 结果:x_0=1.2750 ;x_1=2.4638
可以看到,不同的初值得到了不一样的解,因此fmincon函数不一定能找到最优的解,当然也有解决的方法,那就是取随机数多次求解,但在面对复杂的非线性规划问题,此函数也难以找到最优解。
下面,我们来介绍一下如何用粒子群算法来解决这个问题
七、粒子群算法求解函数的最值
1.粒子群算法中的预设参数
(1) 增加粒子数量会增加我们找到更好结果的可能性,但会增加运算的时间。
(2) 迭代的次数K不一定越大越好,如果现在已经找到最优解了,再增加迭代次数是没有意义的。
(3) 这里出现了粒子的最大速度,是为了保证下一步的位置离当前位置别太远,一般取自量可行域的10%至20%(不同文献看法不同)。
(4) X的下界和上界是保证粒子不会飞出定义域。
n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数
w = 0.9; % 惯性权重
K = 50; % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界
2.初始化粒子的位置和速度
x是一个矩阵,这边我们设置了n个粒子,所以构造n行。列数是我们自变量的维数,如果是多元函数,nars的值就为自变量的个数
之后利用循环,直接使用列向量填充自变量的初始值。
由于我们的vmax与vmin的关系是相反数,因此下方的代码也可以将我们的初值定义在定义域中
x = zeros(n,narvs);
for i = 1: narvs
x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs);
3. 计算适应度(函数值)
这里的适应度其实就是函数值,定义为fit,其为一个n维列向量,代表这n个粒子此刻的函数值
然后利用循环计算出每个粒子的函数值,从中提取出pbest,其为一个n*narvs的向量,代表着迄今为止,每个粒子的所能找到的最佳位置
之后用find函数(用max函数其实也能做到)提取出适应度最大的索引,再将其赋予gbest,得到所有粒子迄今为止找到的最佳位置
这里讲一下find函数的用法,第一个参数是一个向量或者矩阵,第二个参数是一个整数n,返回值是这个矩阵的非0元素的前n个索引。
此处,fit == max(fit)是一个逻辑向量,fit本是一个数值向量,max(fit)是一个数值,而==则把向量中等于max(fit)处的值变成了1,其余的变成了0。这样构造出来了一个逻辑向量
fit = zeros(n,1); % 初始化这n个粒子的适应度全为0
for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度
fit(i) = Obj_fun1(x(i,:)); % 调用Obj_fun1函数来计算适应度(这里写成x(i,:)主要是为了和以后遇到的多元函数互通)
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
ind = find(fit == max(fit), 1); % 找到适应度最大的那个粒子的下标
gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)
4. 粒子轨迹可视化
将散点图的图形句柄赋予给h,之后的迭代步骤中,就可以把迭代后的坐标赋予给h.XData,从而改变坐标,再通过pause(0.1)的操作进行可视化
h = scatter(x,fit,80,'*r');
% scatter是绘制二维散点图的函数,80是我设置的散点显示的大小(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)
5.迭代K次来更新速度与位置
代入迭代公式,并进行判断(1)速度是否超出限制(2)坐标是否超出定义域
fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度
for d = 1:K % 开始迭代,一共迭代K次
for i = 1:n % 依次更新第i个粒子的速度与位置
v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度
% 如果粒子的速度超过了最大速度限制,就对其进行调整
for j = 1: narvs
if v(i,j) < -vmax(j)
v(i,j) = -vmax(j);
elseif v(i,j) > vmax(j)
v(i,j) = vmax(j);
end
end
x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
% 如果粒子的位置超出了定义域,就对其进行调整
for j = 1: narvs
if x(i,j) < x_lb(j)
x(i,j) = x_lb(j);
elseif x(i,j) > x_ub(j)
x(i,j) = x_ub(j);
end
end
fit(i) = Obj_fun1(x(i,:)); % 重新计算第i个粒子的适应度
if fit(i) > Obj_fun1(pbest(i,:)) % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置
end
if fit(i) > Obj_fun1(gbest) % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置
end
end
fitnessbest(d) = Obj_fun1(gbest); % 更新第d次迭代得到的最佳的适应度
pause(0.1) % 暂停0.1s
h.XData = x; % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化)
h.YData = fit; % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化)
end
6.绘制出每次迭代最佳适应度的变化图
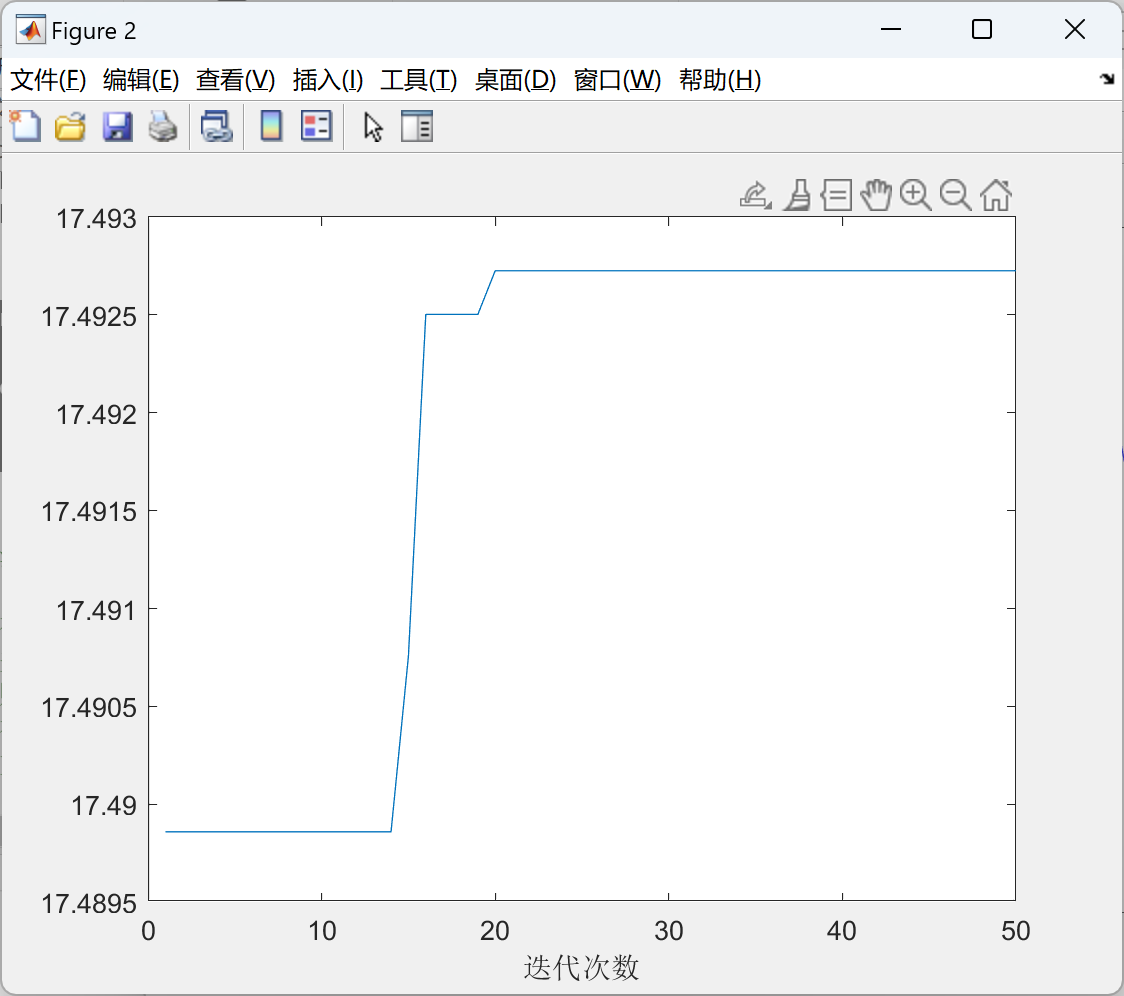
从该图我们可以知道,迭代次数与最佳函数值的变化情况,从该图可以看出,在迭代大约14次的时候,找到了更好的适应度,之后再大约18次又找到了更好的适应度,大约在21次就找到了全局的最大适应度,在此后继续迭代则没有找到更好的适应度了
figure(2)
plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是:'); disp(gbest)
disp('此时最优值是:'); disp(Obj_fun1(gbest))


