2017-2018-20172309 《程序设计与数据结构》第九周学习总结
2017-2018-20172309 《程序设计与数据结构》第九周学习总结
一、教材学习内容总结
一些概念:
- 图: 是一种复杂的非线性数据结构。
- 图的二元组定义:
-
图 G 由两个集合 V 和 E 组成,记为:
G=(V, E) 其中: V 是顶点的有穷非空集合,
E 是 V 中顶点偶对(称为边)的有穷集。 -
通常,也将图 G 的顶点集和边集分别记为 V(G) 和 E(G) 。 E(G) 可以是空集。若 E(G) 为空,则图 G 只有顶点而没有边。
-
- 有向图: 若图 G中的每条边都是有方向的,则称 G 为有向图 (Digraph) 。
- 无向图: 若图G中的每条边都是没有方向的,则称 G 为无向图 (Undigraph) 。
- 完全图:
- 无向图中的每个顶点之间存在着一条边,那么这个图是无向完全图。
- 有向图中的每两个定点之间都存在着方向相反的两条边,则称此图为有向完全图。
- 带权图或网:边上具有权值的图。
- 最小生成树:指的是有一个无向图,根据这个图构造一个包含所有顶点的树,使得包含的边的权值的和最小。
- 最小路径长度:
见下面教材中的问题!
图的储存:
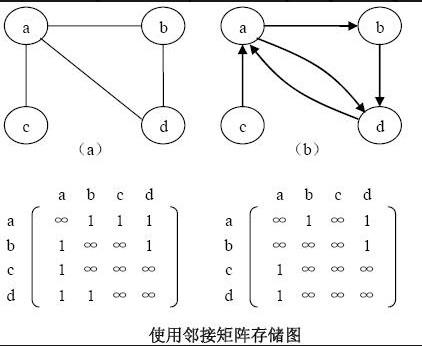
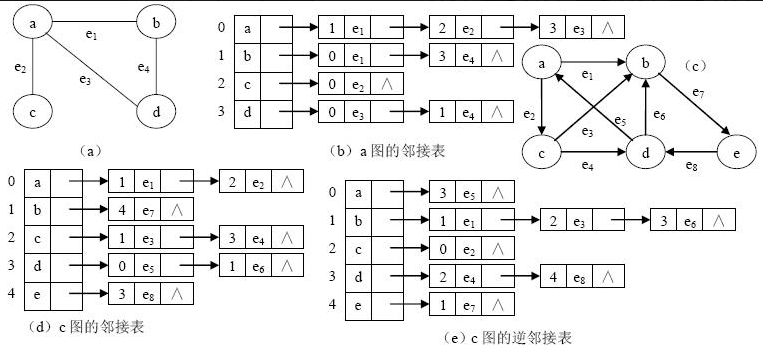
- 邻接矩阵储存法:采用2个数组来表示图;一个是存储所有顶点信息的一维数组(vetices[])、一个是存储图中顶点之间关联关系的二维数组(adjMatrix[][]),这个二维数组称为邻接矩阵。
- 对于无向图a,邻接矩阵是一个对称矩阵,adjMatrix[i][j]==1,说明定点i与定点j是联通的。
- 对于有向图b,当a能到达b时,二维数组adjMatrix[a][b]=1;
- 邻接矩阵的缺点:
- 闲置的单元浪费大量的空间:由n个顶点构成的图中最多可以有n2条边,但大多数情况下,边的数目远远达不到这个量级,因此大多数单元都是闲置的.
- 矩阵结构是静态的,大小N需要预先估计,然后创建N*N的矩阵,而图的规模往往是动态变化的,N估计过大会造成空间浪费,过小则造成空间不够用。
- 邻接矩阵的缺点:
- 邻接列表储存法:对于n个顶点、m条边的无向图,采用邻接表,需要n个表头节点和2m个边表节点。在边数少的情况下,要比使用邻接矩阵节省空间。
- 图的遍历:分为广度优先遍历与深度优先遍历。
二、教材学习中的问题和解决过程
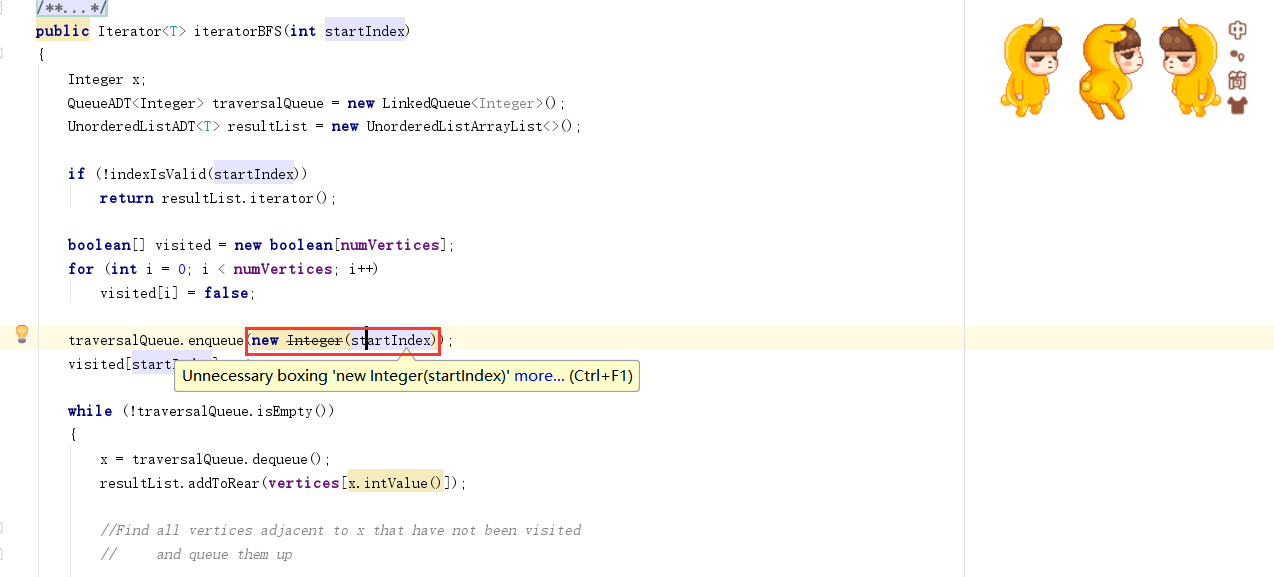
- 问题1:书中有关integer的代码什么意思?
- 问题1解决方案:如图:
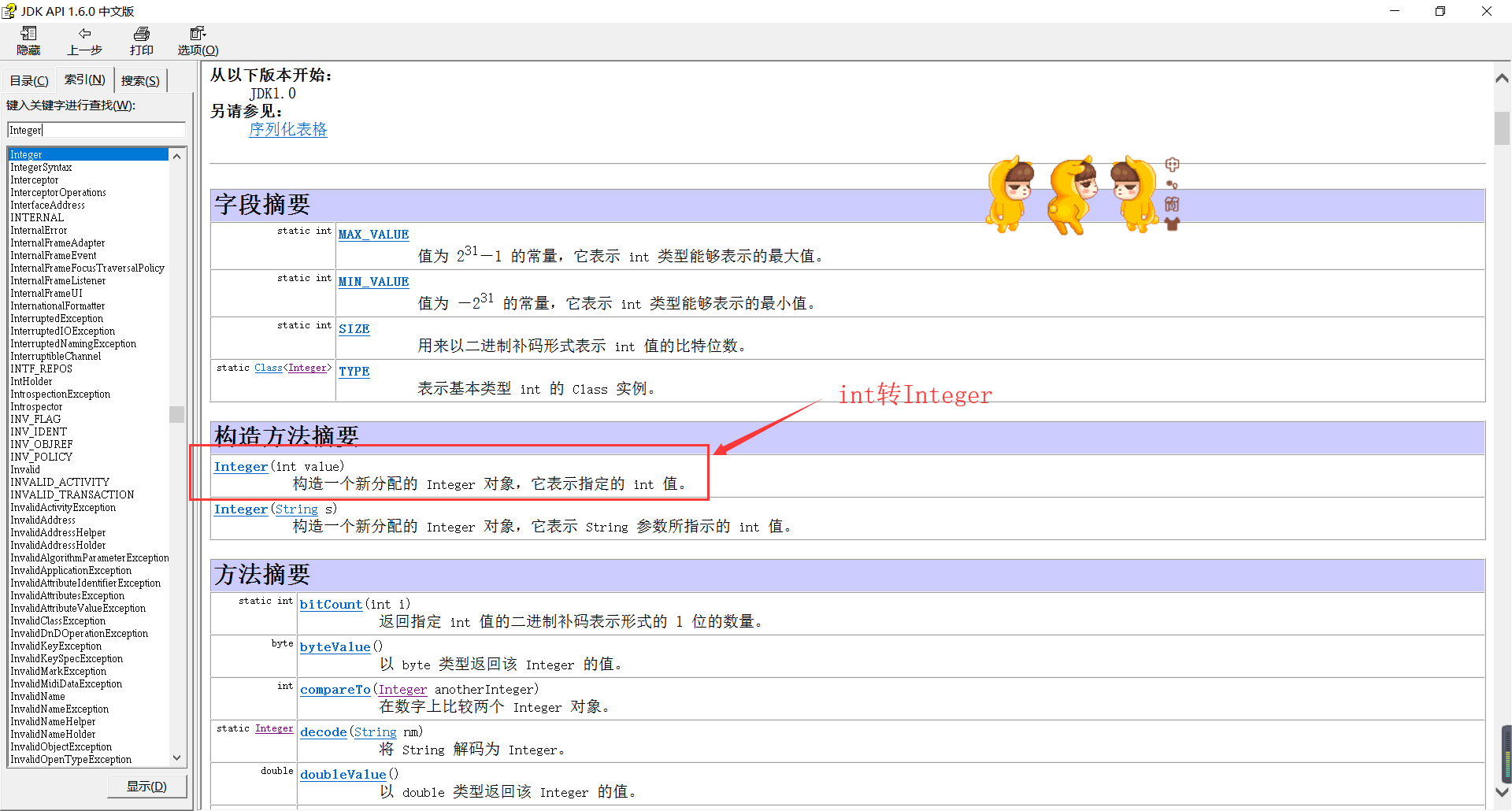
因为队列中储存的数据是Integer类型的,而numVertices是int类型的,因此应该转化为Integer型,对应的方法为:
那么新的问题又来了:为什么一定要Integer,直接用int不好吗?
答案:Integer是其包装类,注意是一个类。而int 是基本数据类型.我们使用integer是为了在各种类型间转化,通过各种方法的调用。
-
问题2:如何理解广度、深度优先遍历?
-
问题2解决方案:
- 广度优先遍历:左看看、又看看,雨露均沾。
- 伪代码:
1. 初始化队列:visited[n] = 0 2. 访问顶点:visited[v] = 1 3. 顶点v加入队列 4. 循环: while(队列是否为空) v = 队列头元素 w = v的第一个邻接点 while(w存在) if(如果w未访问) visited[w] = 1; 顶点w加入队列 w = 顶点v的下一个邻接点 - 深度优先遍历:一条路走到底。
- 伪代码:
1. 访问数组初始化:visited[n] = 0 2. 访问顶点:visited[v] = 1 3. 取v的第一个邻接点w; 4. 循环递归: while(w存在) if(w未被访问过) 从顶点w出发递归执行; w = v的下一个邻接点;
- 广度优先遍历:左看看、又看看,雨露均沾。
-
问题三:如何理解迪杰斯特拉算法?
-
解决方法:
- 感觉这里讲的非常好.
- 所以我还是自己简单总结下吧。
- 这个算法是用来计算两点之间的最短路径的,生活中多用来计算两地之间的来往的最少车费。
- 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
- 举个例子吧:

代码调试中的问题和解决过程
- 问题1:如何判断图的的一个图是否连通?
- 问题1解决方案:
- 如果是连通的,当且仅当使用广度优先遍历中的定点数等于图中的顶点数。
- 因此,我们只要定义一个int值,当每遍历一个顶点,就加一。遍历完成后,看该值是否等于顶点数就OK啦。
- 代码实现
public boolean isConnected() { boolean result = true; for(int i=0;i<numVertices;i++){ int temp=0; temp=getSizeOfIterator(this.iteratorBFS(vertices[i])); if(temp!=numVertices) { result = false; break; } } return result; } - 问题2:完成pp15.1过程中 出现 边不显示、空指针两个问题!
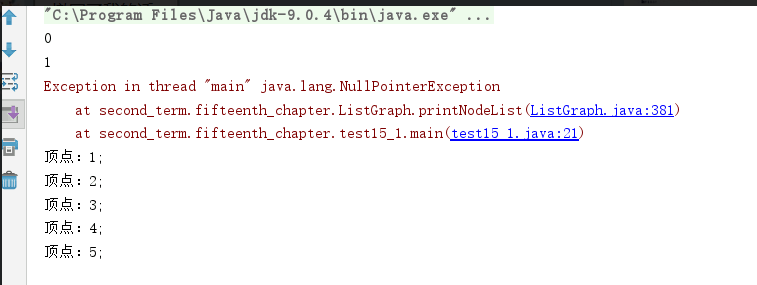
- 问题2解决方案:首先 肯定是 输出方法出现了问题,解决后发现应该这样:

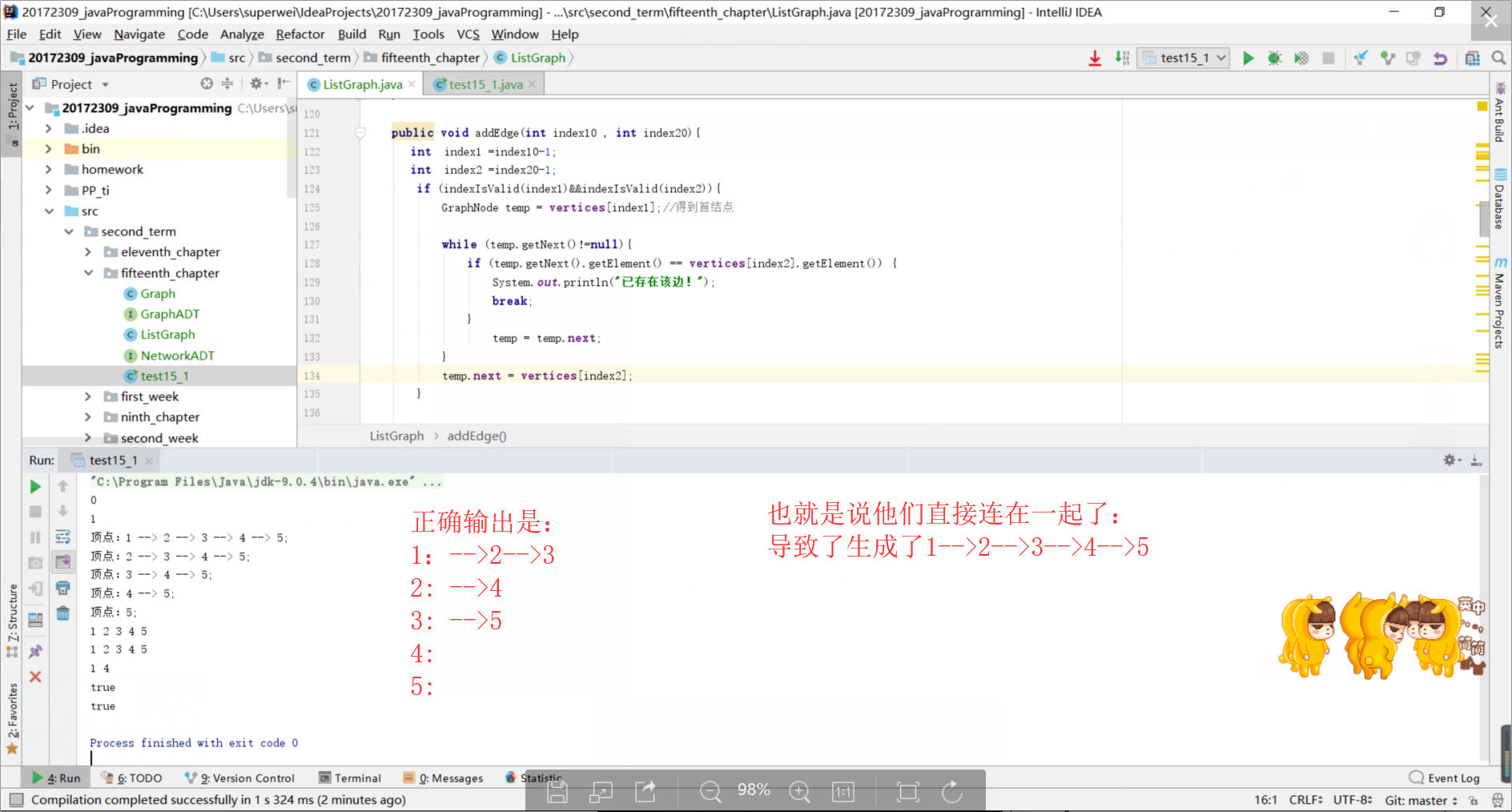
然后出现的问题是:
经分析:肯定是哪句代码错了:导致全部连在一起了!
值得注意的是 在无向图中添加边,应该两边的联系都要考虑:
public void addEdge(int index10 , int index20){
int index1 =index10-1;
int index2 =index20-1;
if (indexIsValid(index1)&&indexIsValid(index2)){
GraphNode temp = vertices[index1];//得到首结点
while (temp.getNext()!=null){
if (temp.getNext().getElement() == vertices[index2].getElement()) {
System.out.println("已存在该边!");
break;
}
temp = temp.next;
}
temp.next = new GraphNode(vertices[index2].getElement());//有index10--》index20
GraphNode temp2 = vertices[index2];
while (temp2.getNext()!=null){
if (temp2.getNext().getElement() == vertices[index1].getElement()) {
System.out.println("已存在该边!");
break;
}
temp2 = temp2.next;
}
temp2.next = new GraphNode(vertices[index1].getElement());//有index20--》index10
}
modCount++;
}
代码之家
课本上的代码:
课后作业代码:
-
pp15.1:
- ListGraph:用邻接列表实现无向图
- test测试类
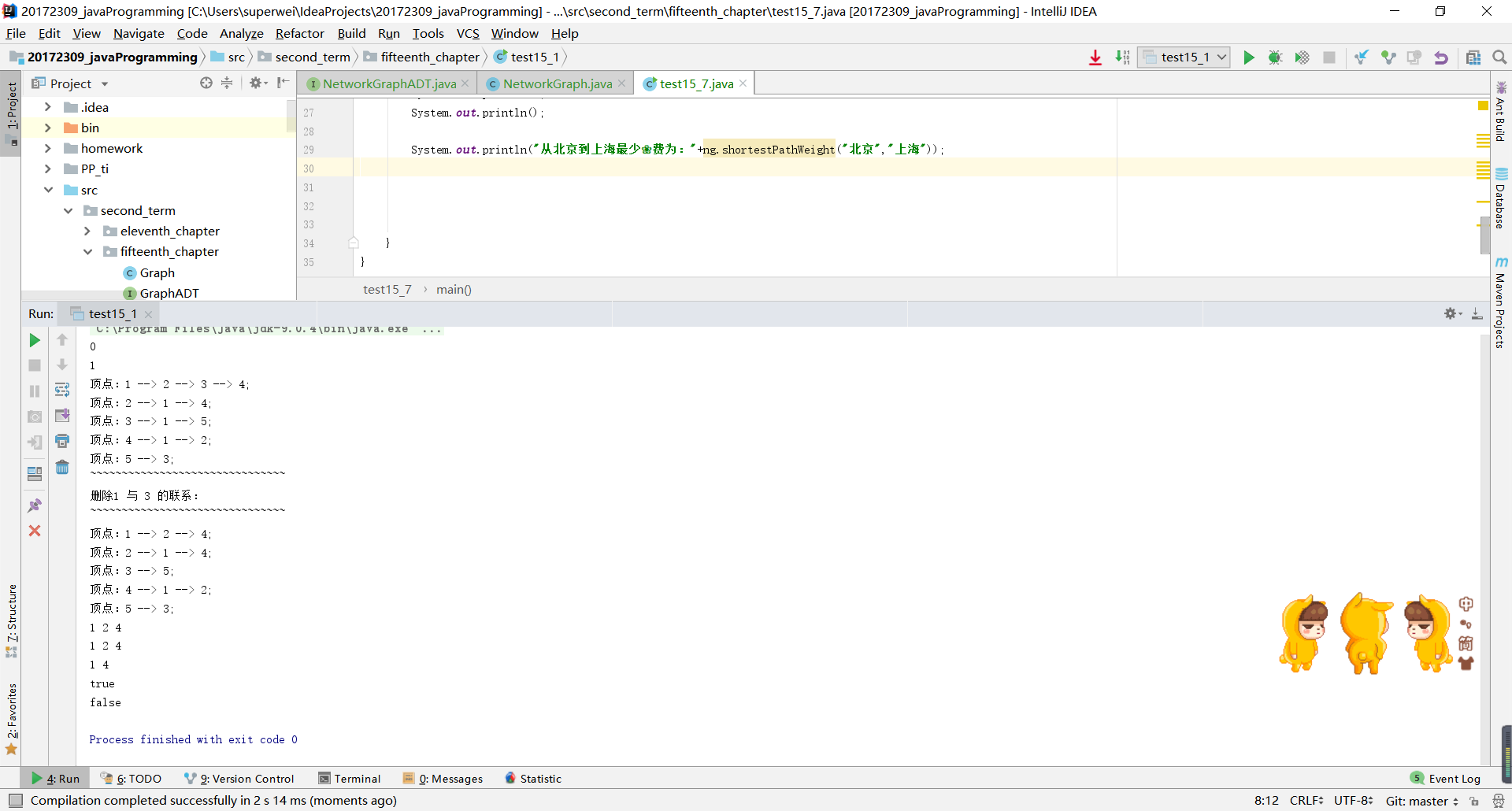
- 实验结果:
-
pp15.7:
- NetworkGraph
- test测试类
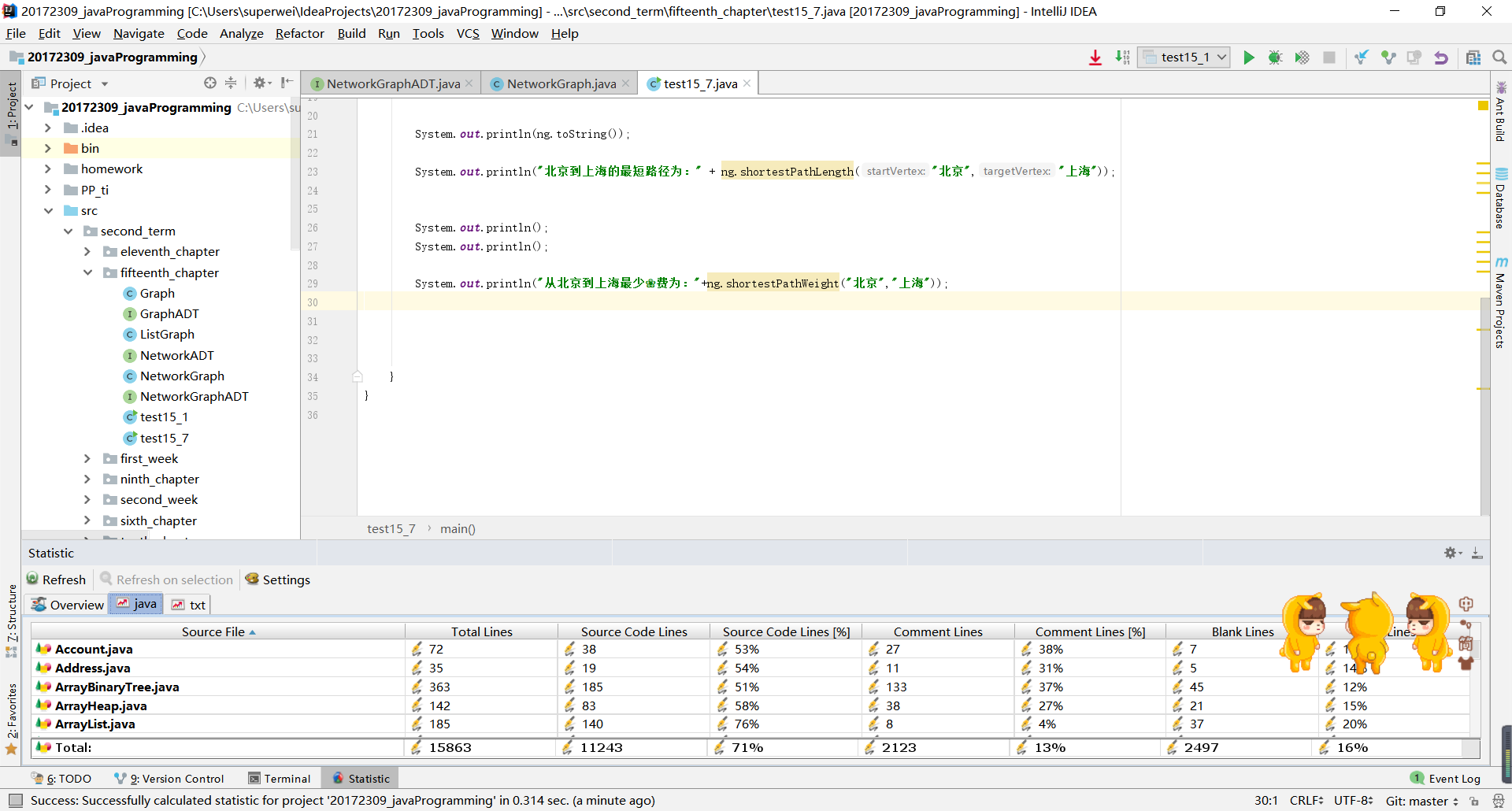
- 实验结果:

代码托管
上周考试错题总结
第十二章错题
Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full. A .True B .Flase错误原因:堆是一棵完全二叉树、不是一颗二叉搜索树。自己瞎了眼!!!!
点评模板:
博客或代码中值得学习的或问题:
- 侯泽洋的博客一直写的很细、很认真、完成的非常早。其中那个最短路程的那个算法写的非常详细,相关资料也给了出来。
- 仇夏和周亚杰的博客也都认真的写了,总觉得自己写的少了点什么东西。
- 向他们学习,相信自己的博客会越来越好。
点评过的同学博客和代码
其他(感悟、思考等,可选)
这一章内容比较简单,或者可以说书上的内容比较简单,但是实现起来很难。也可能是书上的例子比较少的原因。还有就是发现里面的几个算法是非常有意思的,比如Dijkstra算法。它能通过实际的几个数组就能找到最短路径!!!很惊讶!!!
学习进度条(上学期截止7200)
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 260/0 | 1/1 | 05/05 | |
| 第二周 | 300/560 | 1/2 | 13/18 | |
| 第三周 | 212/772 | 1/4 | 21/39 | |
| 第四周 | 330/1112 | 2/7 | 21/60 | |
| 第五周 | 1321/2433 | 1/8 | 30/90 | |
| 第六周 | 1024/3457 | 1/9 | 20/110 | |
| 第七周 | 1024/3457 | 1/9 | 20/130 | |
| 第八周 | 643/4100 | 2/11 | 30/170 | |
| 第八周 | 2800/6900 | 1 /12 | 30/200 |