2017-2018-20172309 《程序设计与数据结构》第八周学习总结
2017-2018-20172309 《程序设计与数据结构》第八周学习总结
一、教材学习内容总结
相信其它很多同学都是以小顶堆来介绍这一章内容,所以我将以大顶堆来介绍这章内容。
1.1 堆的简单介绍:
-
堆的定义:(大顶堆)
- 堆实际上是一棵完全二叉树。
- 堆满足两个性质:
- 堆的每一个父节点都大于其子节点;
- 堆的每个左子树和右子树也是一个堆。
-
堆的分类:
- 堆分为两类:
- 最大堆(大顶堆):堆的每个父节点都大于其孩子节点;
- 最小堆(小顶堆):堆的每个父节点都小于其孩子节点;
- 例子:
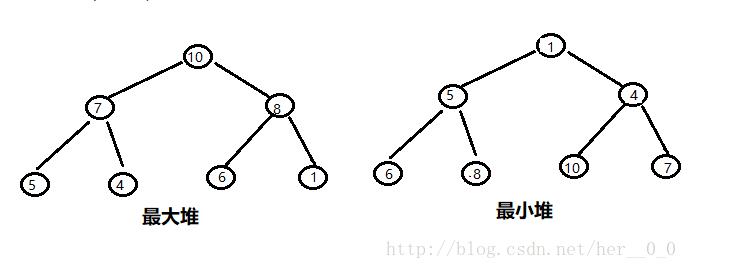
- 堆分为两类:
-
堆的操作:
- 堆的定义是二叉树的拓展,因此他也继承了二叉树的所有操作。
- 操作列表(大顶堆为例):
操作 说明 addElement() 将给定元素添加到该堆中去 removeMax() 删除堆中最大的元素 findMax() 返回一个指向堆中最大元素的引用 -
addElement操作:
- addElement方法将给定的Comparable元素添加到堆中的恰当位置,且维持该堆的完全属性和有序属性。
- 因为堆是一棵完全二叉树,因此对于新插入的节点而言,就只有一个正确的位置,要么是h层左边的下一个空位置,要么是h+1层的第一个位置(此时h层已经装满了)。
- 如下图:它有这两个位置可插入:
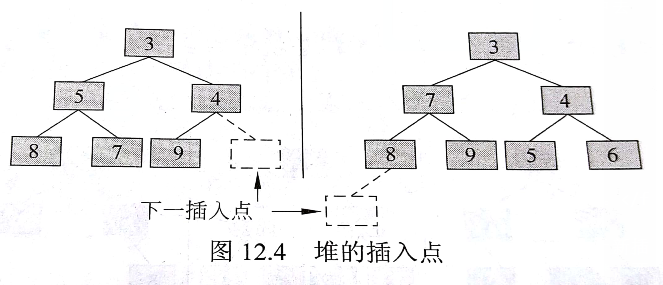
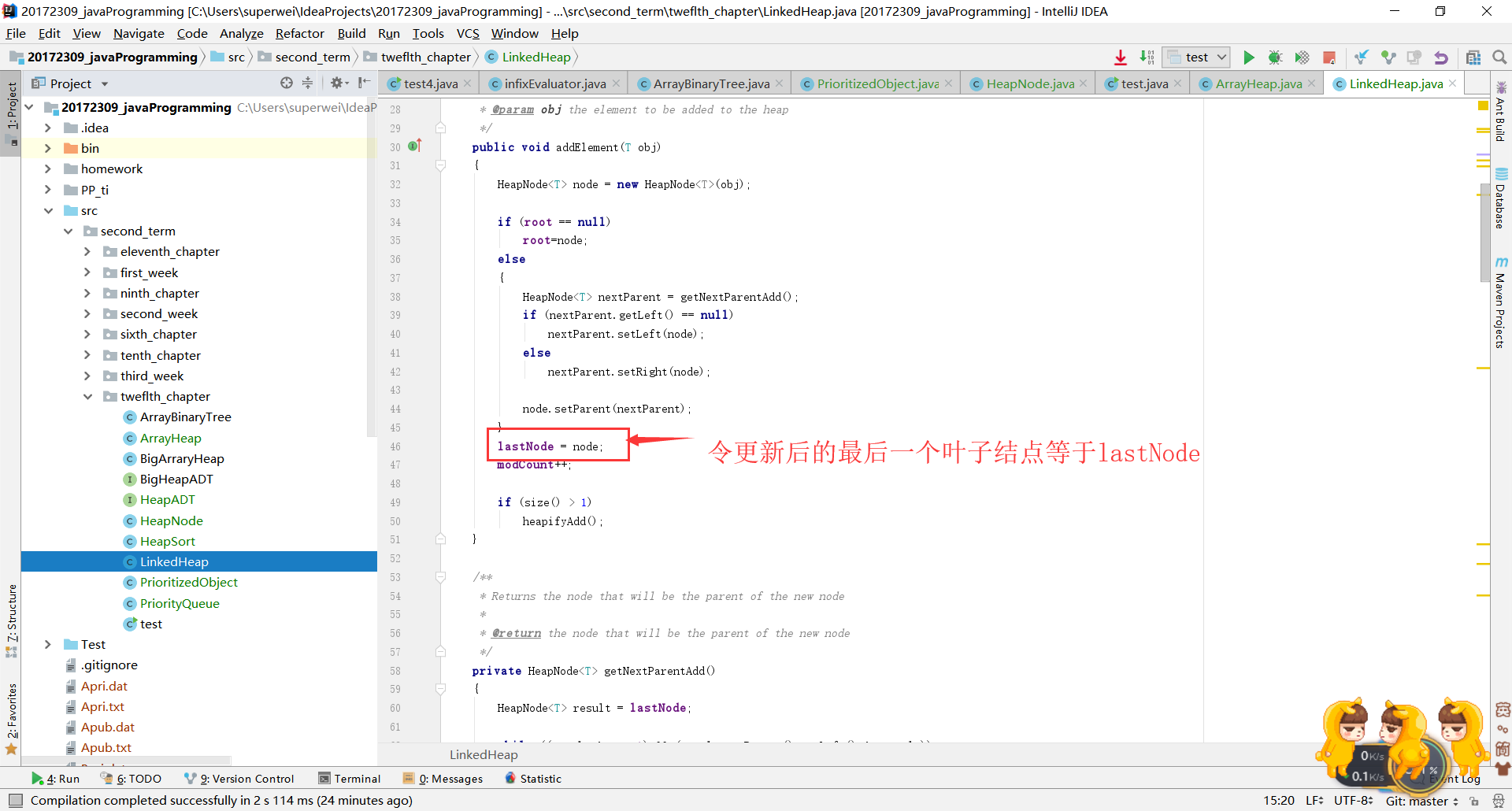
- 通常在堆的实现中,我们会对二叉树的最后一片叶子进行跟踪记录。
- 最大堆的插入:
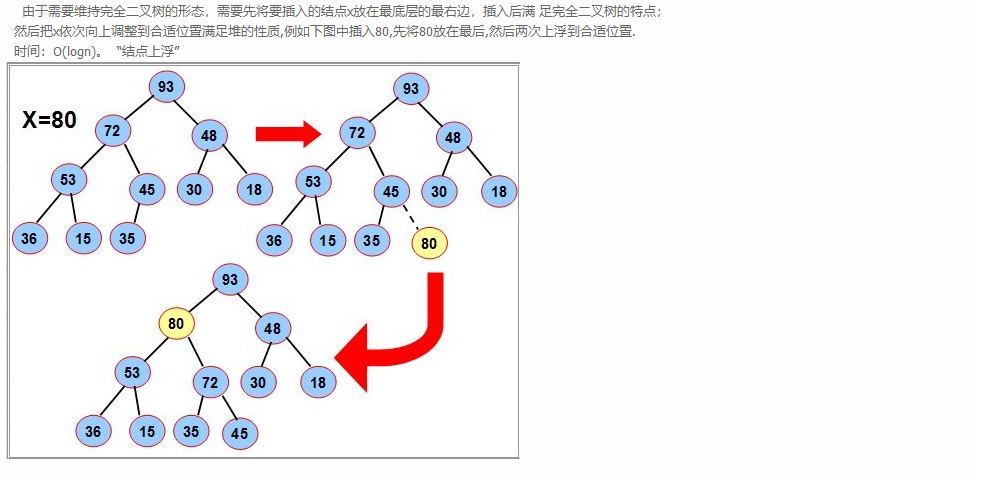
-
removeElement操作:
- 对于大顶堆而言,删除最大元素即删除二叉树的根结点,如果删除根结点而要想维持堆的完全性,必须与最后一片叶子进行交换位置。
- 交换位置后,必须进行重排序、以维持堆的第二个属性:排序。
- 用图表示下过程:
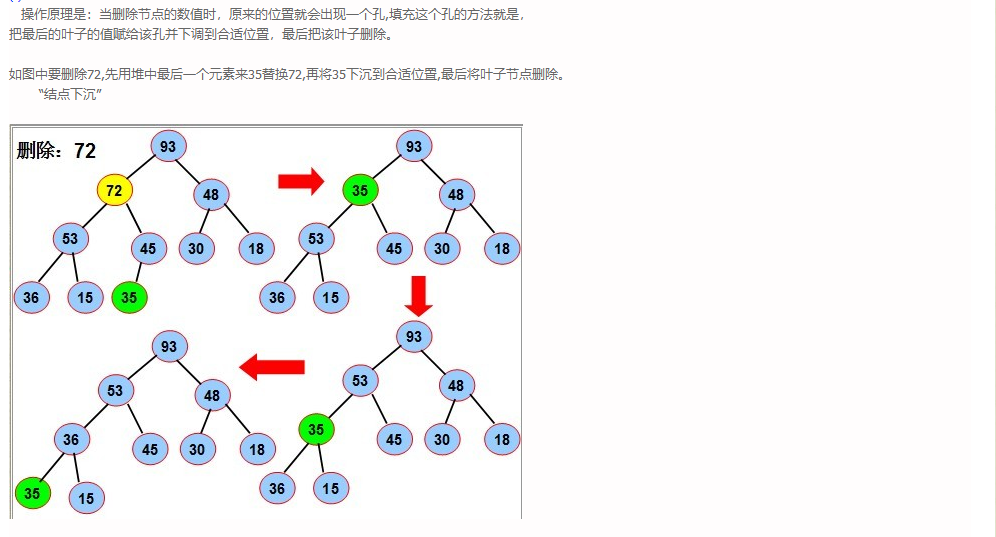
-
findMax操作
findMax操作将返回一个指向该最大堆中最大元素的引用,也就是根结点的引用。所以实现这一操作只需返回储存在根结点的元素即可。
1.2使用堆:优先级队列。
- 我们先来举个例子来感受下优先级队列。
- 生活中,排队时讲究女士优先。
- 游戏中,抽奖人民币玩家获得好东西的概率更大!
- 好,我们现在来说什么是优先级队列:
- 具有更高优先级的项目优先,比如女士、人民币玩家。
- 具有相同优先级的项目使用先进先出的方法 确定其排序。
- 虽然最大堆根本就不是一个队列,但是他提供了一个高效的优先级队列实现。
- 关键代码:
在我看来,这个比较的代码是重中之重的。
public int compareTo(PrioritizedObject obj)
{
int result;
if (priority > obj.getPriority())
result = 1;
else if (priority < obj.getPriority())
result = -1;
else if (arrivalOrder > obj.getArrivalOrder())
result = 1;
else
result = -1;
return result;
}
1.3 用链表实现堆:
- 因为我们需要再插入元素后能够向上遍历树,因此结点中需要一个指向双亲结点的指针。
public class HeapNode<T> extends BinaryTreeNode<T>
{
public HeapNode<T> parent;//指向双亲的指针。
public HeapNode(T obj)
{
super(obj);
parent = null;
}
}
- 我们还需要一个能够跟踪该堆最后一片叶子 的指针:
public HespNode lastNode;
- 最大堆的各种操作:
- addElement操作:
- addElement操作完成三个任务:
- 再恰当位置添加一个元素。
- 对堆进行重排序。
- 将lastNode指针重新指向新的最末结点。
- addElement操作的时间复杂度为:O(log n)
- addElement操作完成三个任务:
- removeMax操作:
- removeMax主要完成三个操作:
- 将最后一片叶子结点与根结点交换位置。
- 对堆进行重排序。
- 返回初始根元素。
- removeMax操作的时间复杂度为:O(log n)
- removeMax主要完成三个操作:
- findMax操作的时间复杂度为O(log n)
- addElement操作:
1.4用数组实现堆:
- 堆的储存一般都是用数组实现的。
- 堆是基于二叉树实现的,在二叉树的数组视线中,对于任一索引值为n的结点,其左结点在2n+1的位置,右结点在2n+2的位置。
- 用数组实现堆的操作与用链表实现堆的操作步骤一样。但值得注意的是:链表实现和数组实现的addElement操作时间复杂度虽然都为O(log n),,但实际上链表更快点。
1.5 使用堆:堆排序。
排序方法有两个部分构成:添加列表的每个元素、一次删除一个元素。
堆排序的时间复杂度为O(log n).
- 进入实战:还记得上次的一个实验,给我们一个数组没让我们形成一个大顶堆,之后让我们排序:现在让我们整理一下思路:
- 首先给出我们一个数组:[45,36,18,53,72,30,48,93,15,35]
- 然后我们应该按照它们的索引形成一个二叉树:
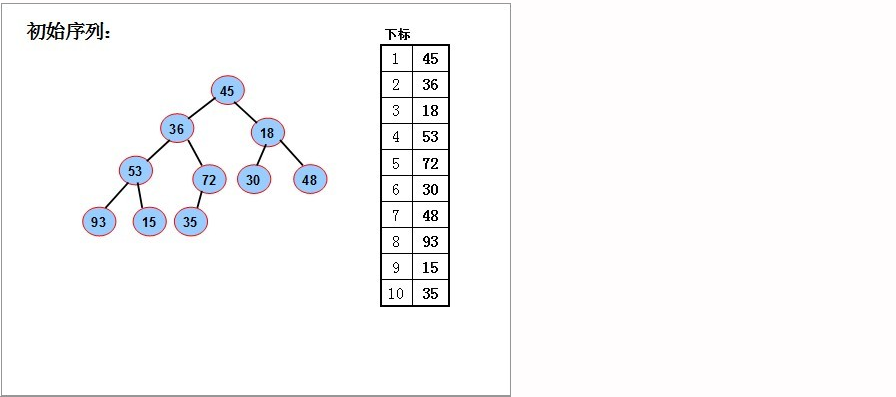
- 然后重排序,得到一个大顶堆:
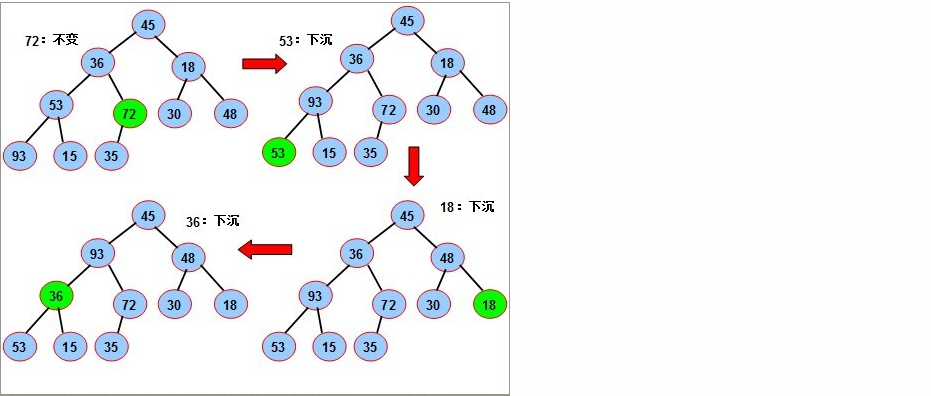

- 每轮排序的结果可以这样表达:
public class test { public static void main(String[] args) { BigArraryHeap<Integer> temp=new BigArraryHeap<Integer>(); int[] list={36,30,18,40,32,45,22,50}; Object[] list2 = new Object[list.length]; //将数组中的元素添加到大顶堆中 for (int i = 0; i < list.length; i++) temp.addElement(list[i]); System.out.println("大顶堆的输出结果为:"+ temp); System.out.println(); for(int n = 0; n < list2.length; n++){ list2[n] = temp.removeMax(); String result = ""; for(int a = 0; a <= n; a++){ result += list2[a] + " "; } System.out.println("第" + (n+1) + "次排序:" + temp + " ~ " + result); } System.out.println(); System.out.print("最后排序结果: "); String result = ""; for(int m = 0; m < list.length; m++){ result += list2[m] + " "; } System.out.println(result); } }- 运行结果为:
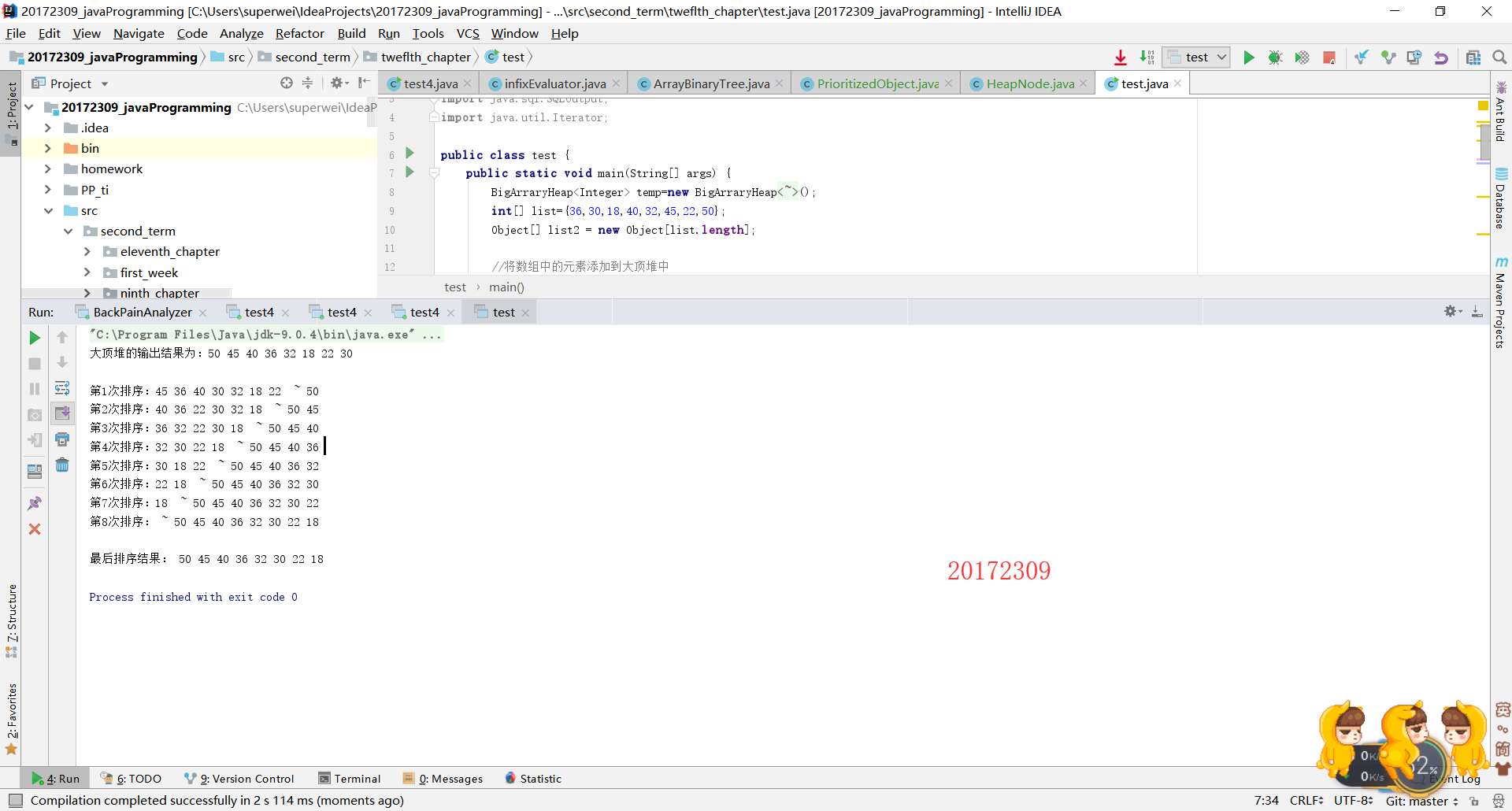
二、教材学习中的问题和解决过程
- 问题1:如何理解这段话,该怎样实现?
通常在堆的实现中,我们会对二叉树的最后一片叶子进行跟踪记录。
- 问题1解决方案:
就是在对堆进行删除操作的时候需要将根结点与最后一片叶子结点进行交换位置,所以每一次操作都得更新lastNode结点。
- 问题2:书上介绍了用数组实现的堆排序,那么链表实现的堆排序应该怎样排序?
- 问题2解决方案:书上数组对对进行排序是写了一个方法,当想要进行排序的时候直接调用这个方法就OK,而我们选在在测试类里面直接进行排序,使用最大堆,取出最大堆输出,然后就可以直接输出。
如图:
- 问题三:在网上搜寻有关于书上的资料室,出现了这么一个尴尬场面:
之后我点进去看了一下:
原来是讲解了有关:栈内存和堆内存。
讲了这么个些东西,来潦草的总结下:
- ava把内存划分成两种:一种是栈内存,一种是堆内存
在函数中定义的一些基本类型的变量和对象的引用变量都在函数的栈内存中分配。 - 当在一段代码块定义一个变量时,Java就在栈中为这个变量分配内存空间,当超过变量的作用域后,Java会自动释放掉为该变量所分配的内存空间,该内存空间可以立即被另作他用。 - 堆内存用来存放由new创建的对象和数组。
- 在堆中分配的内存,由Java虚拟机的自动垃圾回收器来管理。
- 在堆中产生了一个数组或对象后,还可以在栈中定义一个特殊的变量,让栈中这个变量的取值等于数组或对象在堆内存中的首地址,栈中的这个变量就成了数组或对象的引用变量。
- 引用变量就相当于是为数组或对象起的一个名称,以后就可以在程序中使用栈中的引用变量来访问堆中的数组或对象。
(大概就看懂了这么多)
代码调试中的问题和解决过程
- 问题1:如何用堆构建一个队列、栈?
- 问题1解决方案:
首先我们得知道我们必须运用优先级堆,并且每一次添加元素,优先级都加一(从0开始)。
- 然后我们根据队列、栈的特点来输出
- 队列是一种先进先出的结构,所以我们只要使用最小堆中的removeMin方法即可输出最先进去的元素。
- 栈是一种先进后出的结构,所以我们只要使用最大堆中的removeMax方法即可输出最后面进去的元素,因为它的优先级高,所以他在前面输出。
- 结果

- 问题二:符合把一个Object型数据转化为char类型数据?
- 原问题是这样的我需要把
Object operator= +转化为char型数据,但是如果直接转,比如这样(char)operator是会抛出CalssCastException错误的! - 之后解决办法是先转化成String 然后再转化成char类型。
//像这样:
String a = String.valueOf(ope.pop());//ope.pop()出来的是一个Object型数据。
operator = a.charAt(0);
代码之家
- 小顶堆:
- 大顶堆:
- pp项目代码地址:
代码托管

上周考试错题总结
第十章错题
- 错题1及原因:
What type does "compareTo" return? A .int B .String C .boolean D .char错误原因:comparaTo方法返回的是 -1,0,1
而return "a".comparaTo("b")>0为falseorture
第十一章错题
- 无
第十二章错题
Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full. A .True B .Flase错误原因:堆是一棵完全二叉树、不是一颗二叉搜索树。自己瞎了眼!!!!
点评模板:
博客或代码中值得学习的或问题:
- 内容很详细,把堆介绍的很透彻,
- 运用丰富的图片表达思想、比如插入、删除结点的介绍。
- 提出问题有点少。
点评过的同学博客和代码
其他(感悟、思考等,可选)
这一章比起前面相对比较简单,但自己不能松懈.哎,比较难受的是这两天的假期都要贡献给博客了~~~~~o(╥﹏╥)o
学习进度条(上学期截止7200)
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 260/0 | 1/1 | 05/05 | |
| 第二周 | 300/560 | 1/2 | 13/18 | |
| 第三周 | 212/772 | 1/4 | 21/39 | |
| 第四周 | 330/1112 | 2/7 | 21/60 | |
| 第五周 | 1321/2433 | 1/8 | 30/90 | |
| 第六周 | 1024/3457 | 1/9 | 20/110 | |
| 第七周 | 1024/3457 | 1/9 | 20/130 | |
| 第八周 | 643/4100 | 2/11 | 30/170 |
参考资料
1.优先队列
2.堆排序
3.java 各种数据类型之间的转化
4.java中的栈与堆