学号 2018-2019-20172309 《程序设计与数据结构(下)》第一周学习总结
教材学习内容总结
教材学习内容总结
第一章
1. 软件质量:为了最大限度的提高软件质量,高质量的软件具有以下特性:
- 1.1正确性:所设计出的软件必须满足客户的需求。
- 1.2可靠性:就是软件出现故障的次数,高质量的软件很少出现故障。
- 1.3健壮性:完美的健壮系统可以完美的处理各种问题。
- 1.4可用性:用户学习和执行任务的难易程度。
- 1.5可维护性:当想要对软件进行修改时,对软件进行修改的难易程度。
- 1.6可重用性: 软件的组件可用于其他软件系统的难易程度。
- 1.7可移植性:软件可在多种计算机环境下使用的难易程度。
- 1.8运行效率:在占用更少资源的情况下CPU运行的时间。
2. 数据结构:数据结构是一个程序的基础,程序=数据结构+算法。
3. 关键概念:
- 可靠的软件很少发生故障,即使发生了故障,也可以将该故障的影响降到最低。
- 软件系统必须经过精心设计、编码和文档说明,以便为开发人员、维护人员和用户提供支持。
- 软件必须有效使用诸如CPU时间和内存之类的内存。
- 质量特性必须优先考虑,并尽可能最大化。
- 栈可用于颠倒数据集的顺序、队列可以保持其数据的顺序。
第二章
1.算法效率:软件质量的特征之一是资源的使用效率,CPU的使用时间是最重要的资源之一。算法分析是计算机科学的基础。
2.增长函数与大O记法:
- 1.1增长函数标识问题(n)大小与我们希望最优化的值之间的关系。该函数表示了该算法的时间复杂度或空间复杂度。
- 1.2我们主要看重的是渐进复杂度,又称为阶次。例如:在t(n)=15n²+45n中,当n逐渐变大时,一次项几乎不计。故阶次为n²
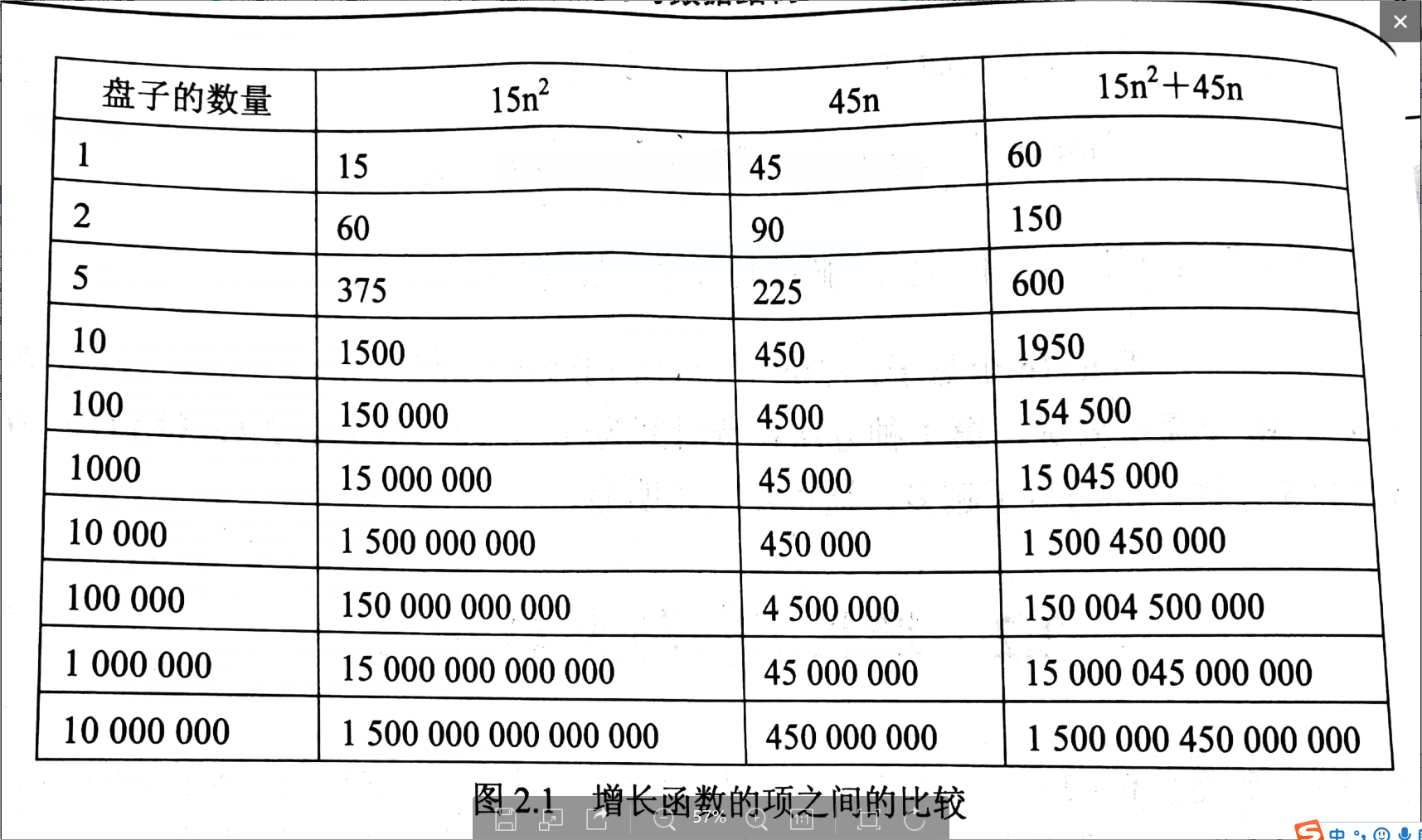
3.时间复杂度的分析:
- 3.1 要分析算法的复杂度,通常要分析循环的运行。
- 3.2 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
- 3.3 几个相关的例题
// 例题一
for (int count = 0 ; count < n ; count++)
{
//复杂度为O(1)的步骤系列
}
//答案:循环体复杂度*循环运行次数=O(1)*O(n)=O(n)
//例题二:嵌套循环的复杂度分析
for (int count = 0 ; count < n;count++)
{
for ( int count2 = 0 ; count2<n ; count2++)
{
/*复杂度为0(1)的步骤系列*
}
}
//答案:外层循环次数*内层循环次数*循环体=O(n)*O(n)*O(1)=O(n²)
//要点:分析嵌套循环的复杂度时,必须将内层循环和外层循环都考虑进来。
//例题三
for ( int count = 0 ; count < n ; count++)
{
for ( int count2 = count ; count2 < n ;count2++)
{
//复杂度为O(1)的步骤系列
}
//此段代码需注意:外层复杂度为O(n),而内层运行次数分别是n , n-1 , n-2 , ... , 1.而我们又必须知道:我们只对主项感兴趣,即只关心最大的。所以答案是O(n²)
}
- 3.4 方法调用的复杂度分析:
- 记住,只有可运行的语句才会增加时间复杂度。
例如:
for ( int count = 0 ; count < n ;count++ )
{
printsum(n);
}//此处只知道外层循环次数,不知道内层方法。不能知道此程序的复杂度。
- 还有一个比较难的题目:
public void sample ( int n )
{
printsum(n); /*该方法的复杂度为O(1)*/
for ( int count = 0 ; count < n ; count++)
printsum(count);
for (inr count = 0 ; count < n ; count++)
for ( int count2 = 0 ;count2 < n ;count2 ++)
System.out.println(count,count2);
}
我们可以这样想:
public void sample ( int n )
{
printsum(n); //O(1)
for ( int count = 0 ; count < n ; count++)
printsum(count);// O(n)
for (inr count = 0 ; count < n ; count++)
for ( int count2 = 0 ;count2 < n ;count2 ++)
System.out.println(count,count2); //O(n²)
}//用数学来思考即: O(1)+O(n)+O(n²) 因为我们只关注主项,所以阶次为O(n²)
3.关键概念
- 软件必须有效地使用诸如CPU时间和内存之类的资源。
- 算法分析是i计算机科学的基础。
- 增长函数表示与该问题大小相对应的时间或空间的使用。
- 算法的阶次是忽略该算法的增长函数中的常量和其他次要项,只保留主项而得出的。
- 算法的阶次为增长函数提供了一个上界。
- 如果算法的运行效率低, 那么从长远米说, 使用更快的处理器也无济于事。要分析算法的复杂度,通常需要分析循环的运行。
- 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。分析嵌套循环的复杂度时,必须将内层循环和外层循环都考虑进来。
读课本遇到的疑惑:
-
- 为何说阶次的算法给增长函数提供了一个上界?
-
觉得这张图能很好解决这个问题:
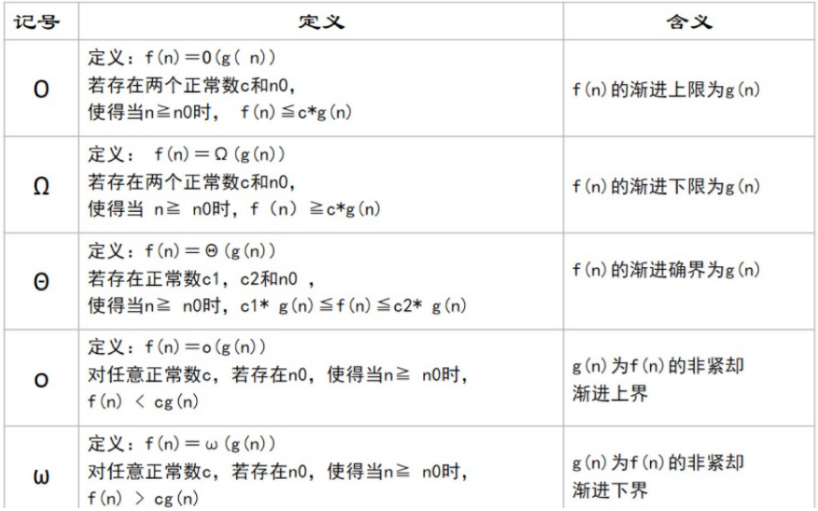
-
2.在书中例题:
count = 1;
while (count < n )
{
count *= 2;
}
此程序的阶为什么是O(log2 N)而不是O(log2 n/count)?
- 手写方便些:
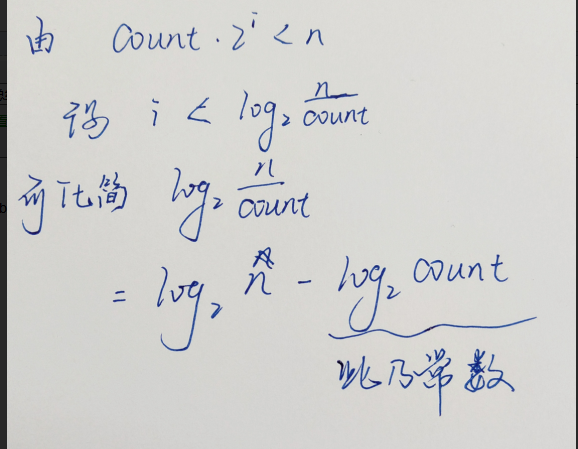
点评模板
- 我的伙伴:仇夏20172310
感想
- 新的学期开始了,没想到第一周就得写博客。蓝瘦香菇····· 但不管怎样还是希望自己能学好这门课程,加油吧!!!


