20172309 《Java软件结构与数据结构》实验三报告
课程:《程序设计与数据结构(下)》
班级:1723
姓名: 王志伟
学号:20172309
实验教师:王志强老师
实验日期:2018年11月2日
必修/选修: 必修
实验内容:
实验一:
实验二:

实验三:

实验四:
实验五:

实验过程及结果:
实验一:
- 定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169)。
- Searching类的实现linearSearch方法。
这个算法的理念是一个一个查找,直到找到为止。不过个人觉得这个算法的缺点是当有两个目标值时,将不会查到第二个。比如:在数组{1,2,3,4, 5, 5,6 }中查找数字5时,将只能查找到索引为4的数字5,而不会查找到索引值为5的那个。public static <T> boolean linearSearch(T[] data, int min, int max, T target) { int index = min; boolean found = false; while (!found && index <= max) { found = data[index].equals(target); index++; } return found; }//顺序/线性查找- 测试代码:

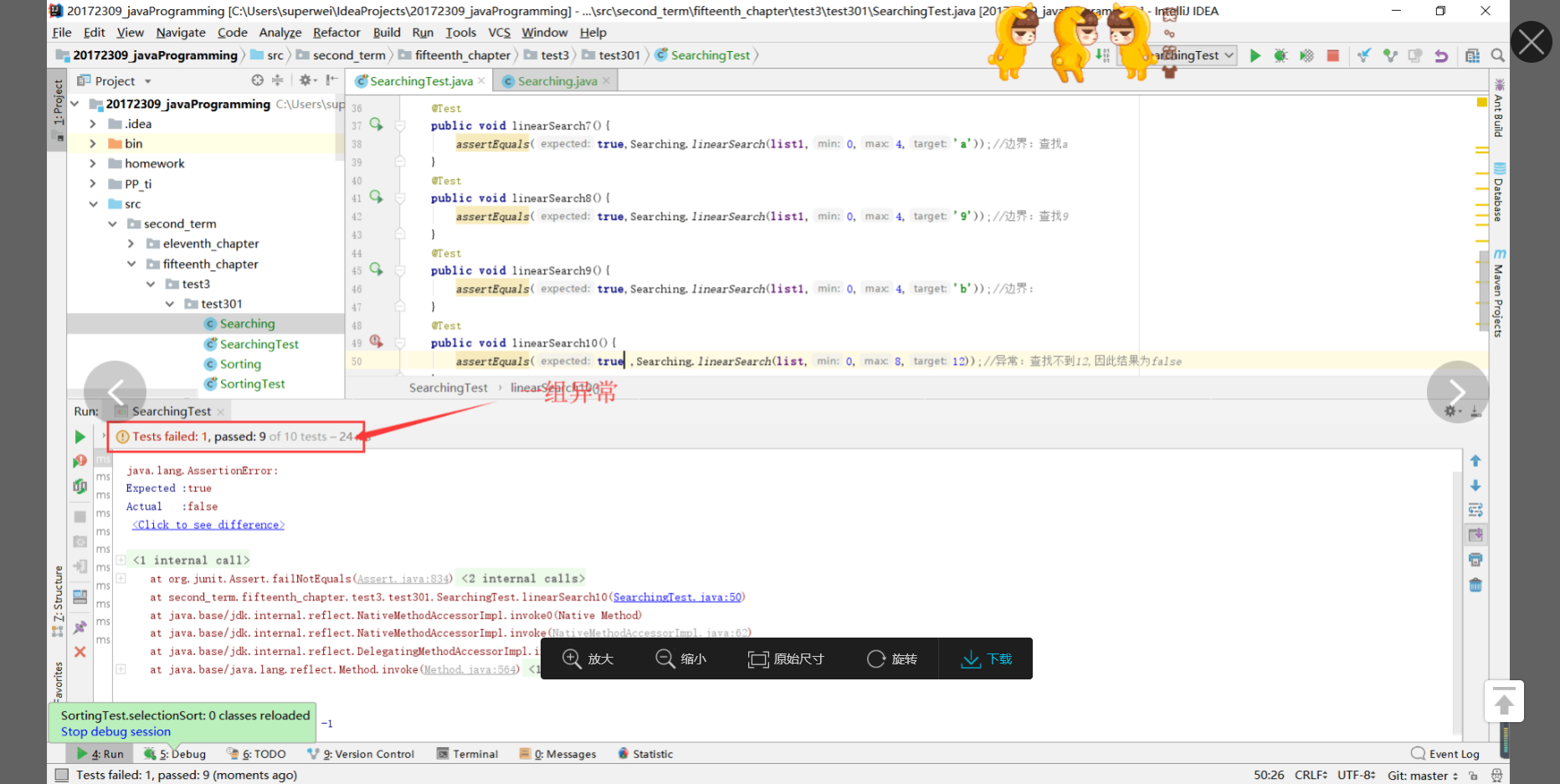
- 测试结果:
- Sorting的selectsort方法:
选择排序的理念就是把一排数列中的东西中的最大(最小)放到最前面并与之交换位置,之后又从剩下的算法中选择出最大(最小)的与第二个项目交换位置·····直至全部完成。这里值得说的一个重点是public static <T extends Comparable<T>>//选择排序 String selectionSort(T[] data) { int min; T temp; for (int index = 0; index < data.length - 1; index++) { min = index; for (int scan = index + 1; scan < data.length; scan++) if (data[scan].compareTo(data[min]) < 0) min = scan; swap(data, min, index); } return Arrays.toString(data); }Arrays.toString(data);这个方法,这个方法的用处是把一个数组自动ToString(),也就是不用自己写toString方法。- 代码截图:
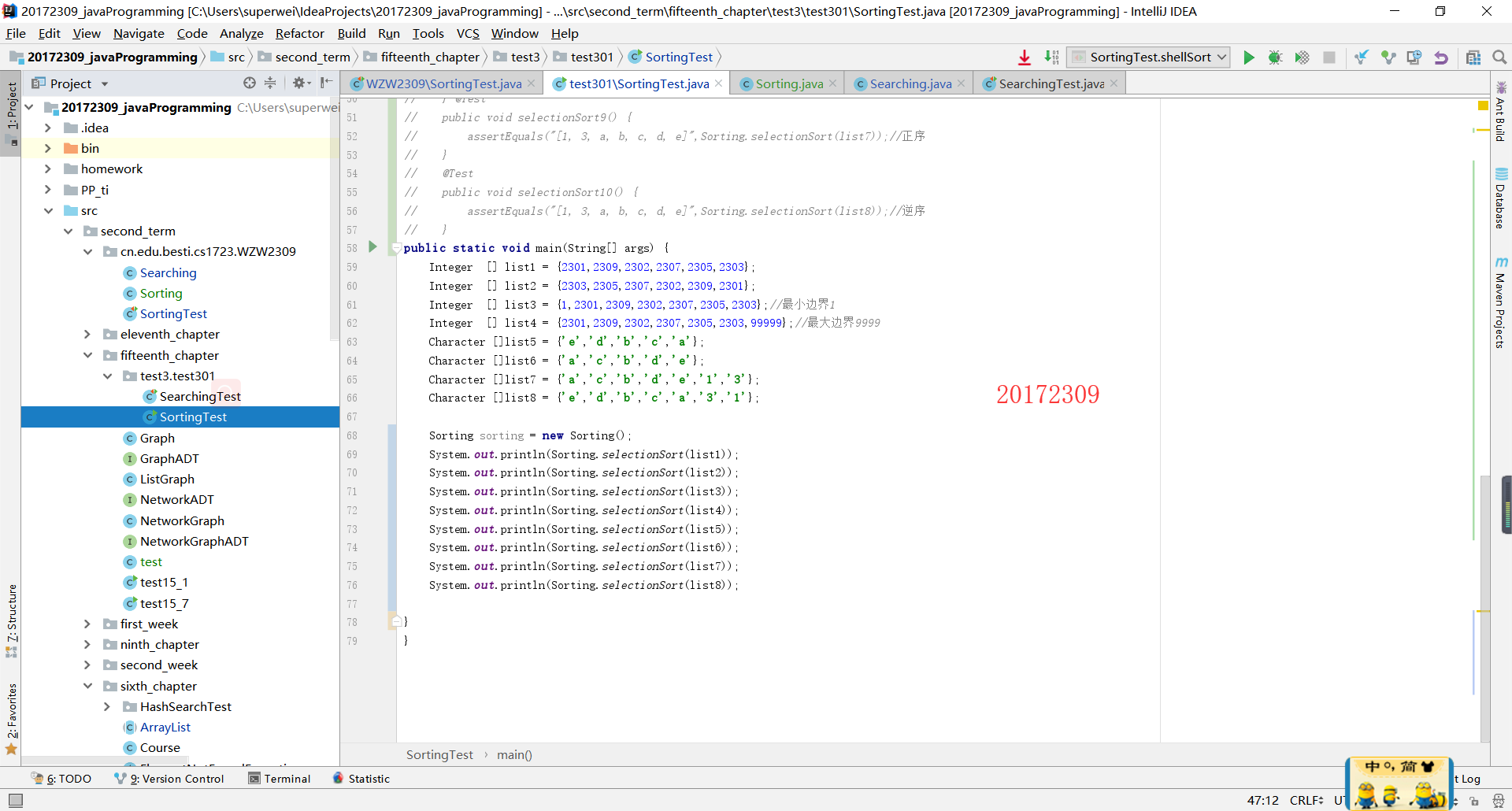
- 结果截图:
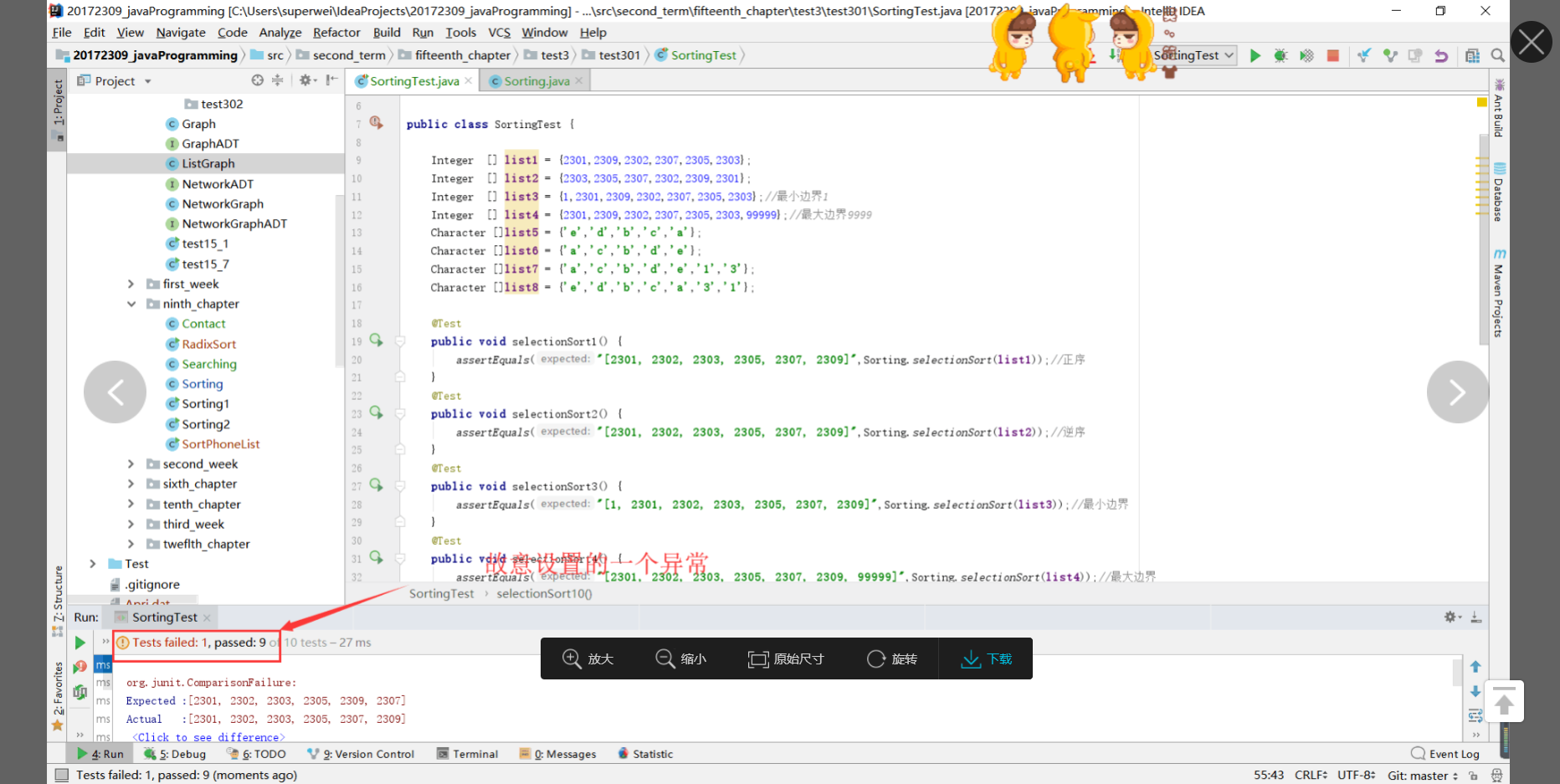
- 要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位。
- 这里要求测试用例需要正常、异常、边界、正序、逆序我感觉有点错误,比如线性查找哪来的正序、逆序测试,选择排序哪来的边界测试。不是很懂,感觉有问题~~~
实验二:
- 把Sorting.java,Searching.java放入cn.edu.besti.cs1723.(姓名首字母+四位学号)包中(例如:cn.edu.besti.cs1723.G2301)。并把测试代码放test包中。
一开始并不知道
cn.edu.besti.cs1723.什么意思,其实到文件中去看就会发现他这并不是一个文件夹,而是cn的文件夹下有edu,edu的文件夹下有besti....
- 重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种)
- 用IDEA测试结果与实验一一样,因此在这不放图。
- 用命令行进行测试:由于老师没有明确表达必须使用Junit测试,因此我选择了使用main函数测试(因为虚拟机使用命令行还得安装一个Junit.jar包~~~ 而安装包的什么命令都是上学期的事儿了,哪还记得 ?)。
查找结果:
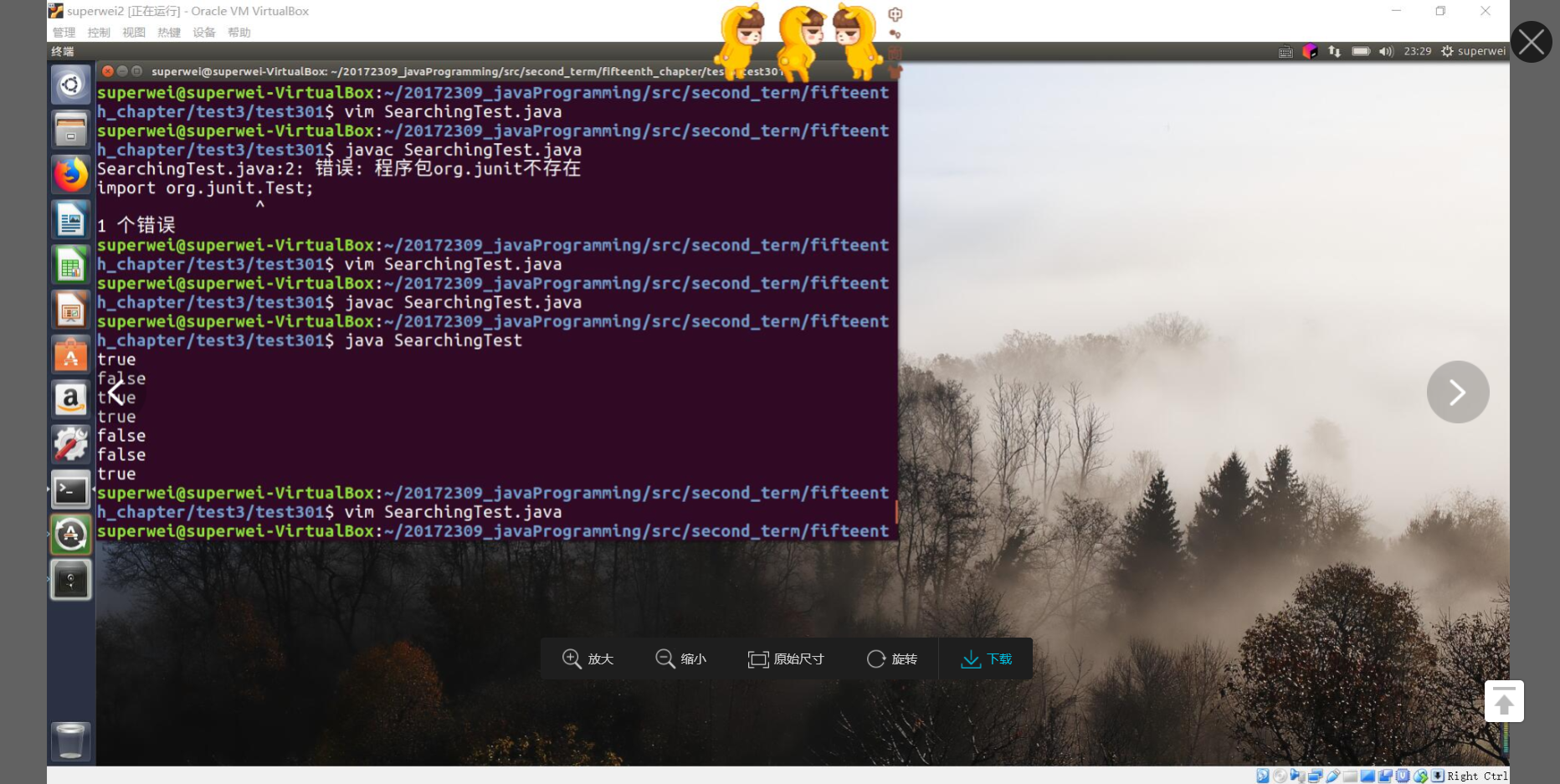
排序结果:
- 开心的是好像IDEA也有命令行模式,不过这是在我做完实验之后才发现的o(╥﹏╥)o
如果没有显示的话,可以手动开启:
实验三:
-
参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试提交运行结果截图。我们将一个个讲解下查找算法:以前在博客中讲过的一笔带过,没讲的是重点
- 顺序查找:
- 主要思想:顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。说明:顺序查找适合于存储结构为顺序存储或链接存储的线性表。
- 时间复杂度为:O(n)
- 方法代码:
public static <T extends Comparable<T>> boolean binarySearch(T[] data, int min, int max, T target) { boolean found = false; int midpoint = (min + max) / 2; // determine the midpoint if (data[midpoint].compareTo(target) == 0) found = true; else if (data[midpoint].compareTo(target) > 0) { if (min <= midpoint - 1) found = binarySearch(data, min, midpoint - 1, target); } else if (midpoint + 1 <= max) found = binarySearch(data, midpoint + 1, max, target); return found; }//二分查找- 二分查找:
- 主要思想:也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。元素必须是有序的,如果是无序的则要先进行排序操作。
- 时间复杂度:O(log2n)
- 方法代码:
public static <T extends Comparable<T>> boolean binarySearch(T[] data, int min, int max, T target) { boolean found = false; int midpoint = (min + max) / 2; // determine the midpoint if (data[midpoint].compareTo(target) == 0) found = true; else if (data[midpoint].compareTo(target) > 0) { if (min <= midpoint - 1) found = binarySearch(data, min, midpoint - 1, target); } else if (midpoint + 1 <= max) found = binarySearch(data, midpoint + 1, max, target); return found; }//二分查找- 插值查找:
- 主要思想:
- 基于二分查找,属于有序查找,相对于二分查找有时能够提升效率。
- 对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
- 个人觉得最重要的就是这个了:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low)为什么是这样?在下面的的问题中讲。
- 时间复杂度:查找成功或者失败的时间复杂度均为O(log2(log2n))。
- 方法代码:
public static boolean interpolationSearch(int[] data,int low,int high,int target){ while (low<high) { int mid=low+(high-low)*((target-data[low])/(data[high]-data[low])); if (target<data[mid]) { interpolationSearch(data, low, mid-1, target); } else if (target>data[mid]) { interpolationSearch(data, mid+1, high, target); } else { return data[mid]==target; } } return false; - 主要思想:
}//插值查找,不能使用泛型
```- 斐波那契查找:
- 主要思想:也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法。
- 斐波那契查找算法
- 时间复杂度:O(log2n)
- 方法代码:
public static boolean FibonacciSearch(int[] data,int target){ int low = 0; int high = data.length - 1; int mid = 0; // 斐波那契分割数值下标 int k = 0; // 序列元素个数 int count = 0; // 获取斐波那契数列 int[] f = new int[20]; int m = 0; f[0] = 1; f[1] = 1; for (m = 2; m < 20; m++) { f[m] = f[m - 1] + f[m - 2]; } // 获取斐波那契分割数值下标 while (data.length > f[k] - 1) { k++; } // 创建临时数组 int[] temp = new int[f[k] - 1]; for (int j = 0; j < data.length;j++){ temp[j] = data[j];
}
```- 二叉树查找:
- 主要思想:
- 二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。
- 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
- 对二叉查找树进行中序遍历,即可得到有序的数列。
- 时间复杂度:它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。
- 方法代码:
详情看上面链接 - 主要思想:
- 分块查找:
- 主要思想:将n个数据元素"按块有序"划分为m块(m ≤ n)。每一块中的结点不必有序,但块与块之间必须"按块有序";即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;而第2块中任一元素又都必须小于第3块中的任一元素,……
- 算法步骤:
- 先选取各块中的最大关键字构成一个索引表;
- 查找分两个部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;然后,在已确定的块中用顺序法进行查找。
- 时间复杂度:
- 方法代码:
//详情看上面链接 - 哈希查找:
- 主要思想:哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键
- 算法步骤:
- 用给定的哈希函数构造哈希表;
- 根据选择的冲突处理方法解决地址冲突;常见的解决冲突的方法:拉链法和线性探测法。详细的介绍可以参见:浅谈算法和数据结构: 十一 哈希表。
- 在哈希表的基础上执行哈希查找。
- 时间复杂度:O(1)
- 方法代码:
//详情看上面链接
- 顺序查找:
实验四:
- 补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个),测试实现的算法(正常,异常,边界)。
- 希尔排序:
- 主要思想:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
- 举个例子:
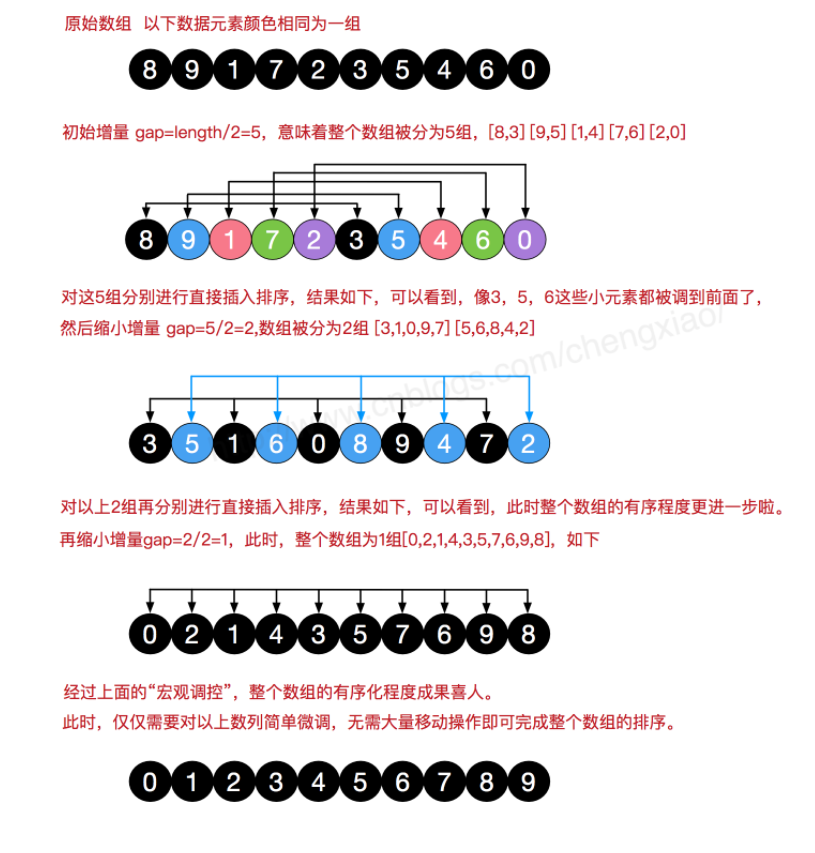
- 堆排序:
- 这个因为以前就写好了最小堆,每次把最小的顶堆取出来,就完成了从小到大的排序。
- 二叉排序:
- 和上面一样,因为二叉查找树的左子树小于或等于父结点,父结点小于或等于右结点。所以使用中序遍历就可以完成从小到大的排序。
- 代码截图:
- 提交运行结果截图。
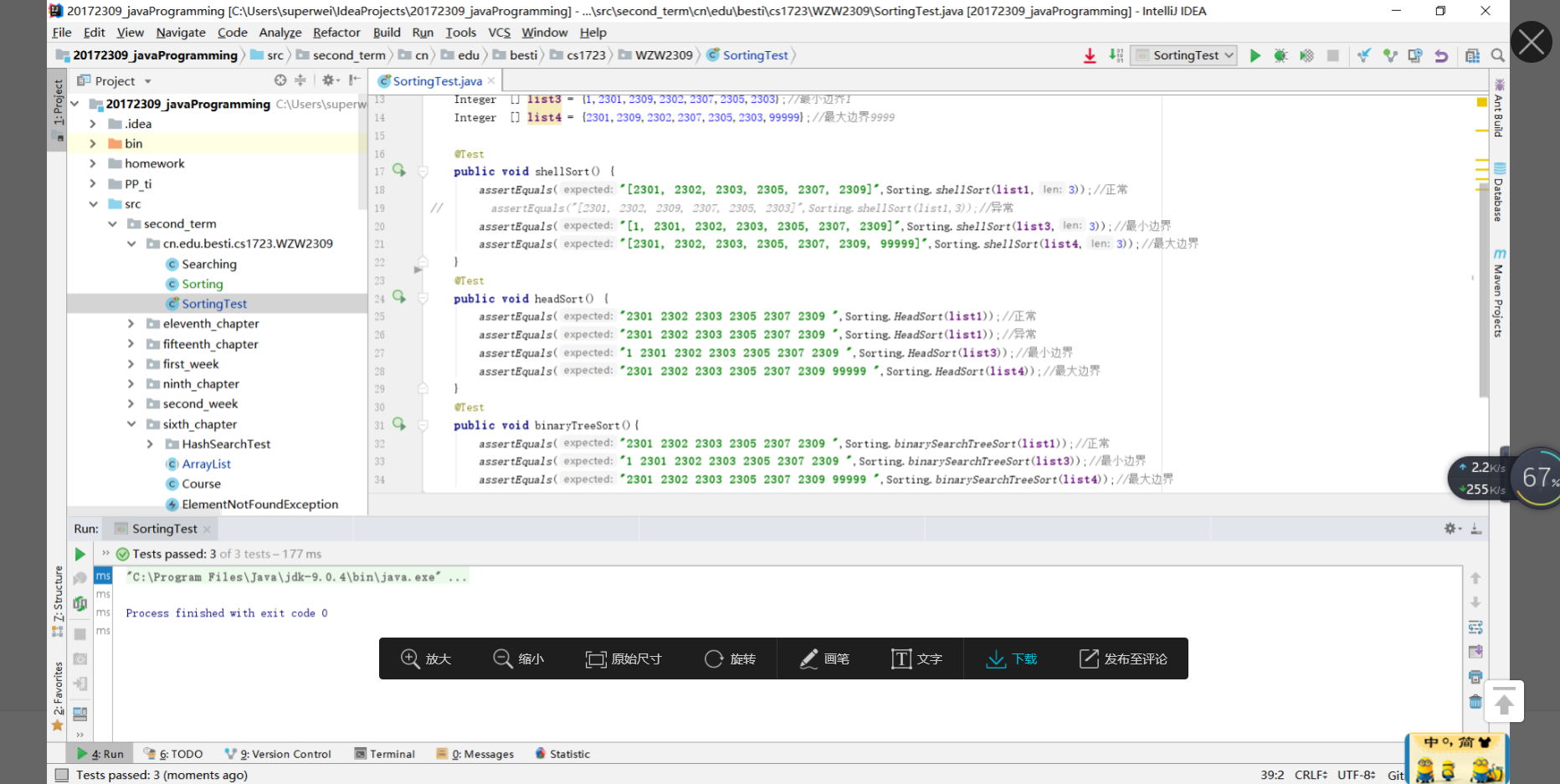
- 希尔排序:
实验五:
- 编写Android程序对各种查找与排序算法进行测试
- emmm·····本来看到这的时候就准备使用一个下拉列表的,但是做了四五个小时后发现出现了bug,所以为了提交作业只好提交了一种比较low的方法。
- 运行结果:
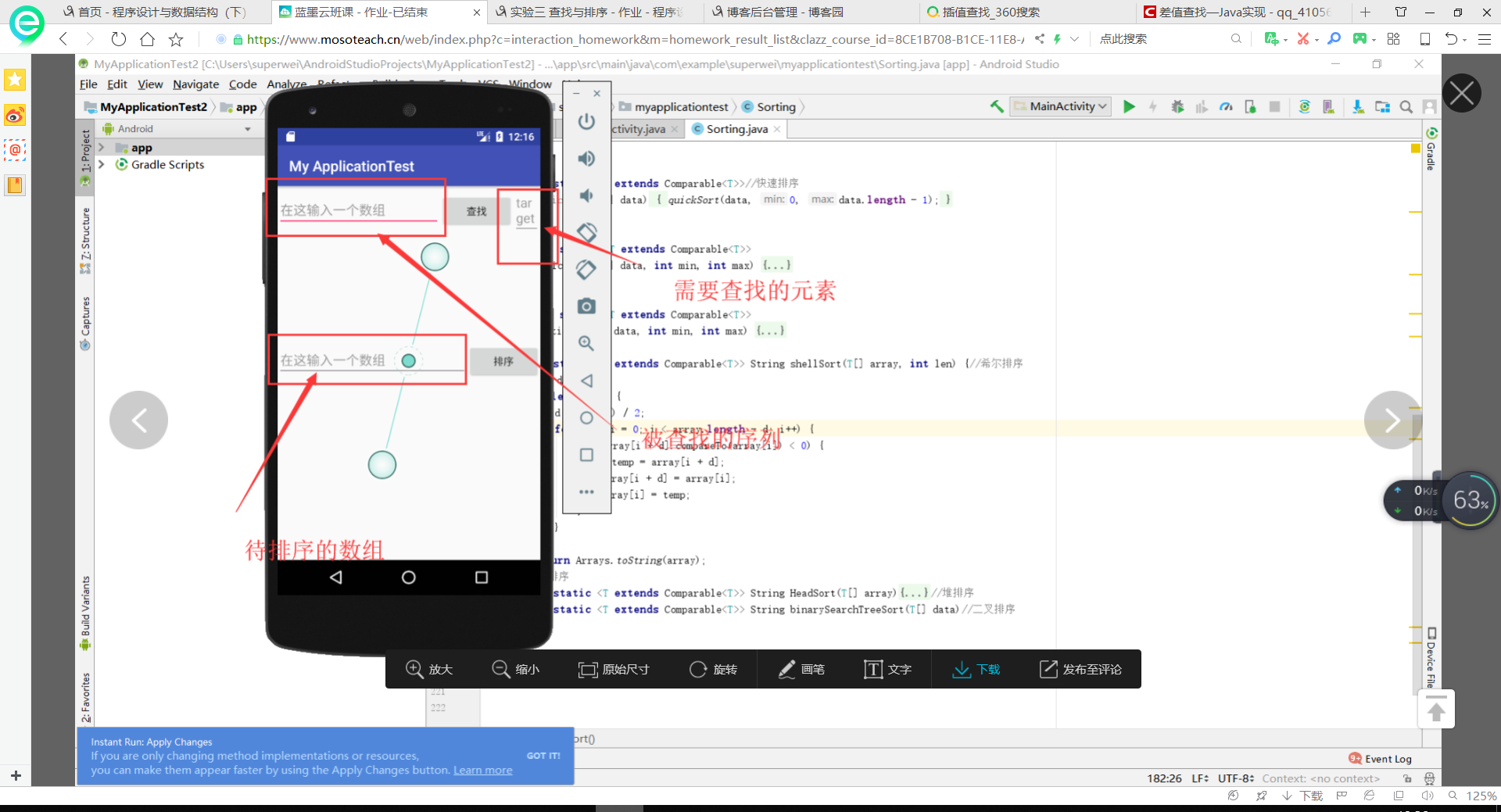
- 测试结果:

- 不过在这里学到了一种比较好用的方法:
- 在xml文件中编写按钮Button控件时,可以使用
onclick属性。像这样:
<Button android:layout_width="wrap_content" android:layout_height="wrap_content" android:text="创建数据库" **android:onClick="creatDb"**<--这儿 android:background="#ffbbff" />- 那么这个方法有什么用呢?
个人总结就是当有很多按钮时,我们不必每个按钮都写点击事件了只要写一个就OK了,例:
public void onclick(View view){ switch (条件){ case R.id.button1: ···逻辑代码··· break; case R.id.button2: ···逻辑代码··· break; ····· } - 在xml文件中编写按钮Button控件时,可以使用
试样过程中遇到的问题:
-
问题一:如何进行Junit测试?
-
问题一解决方案:现在自己来总结下吧。
- emmm·····,首先选中要进行Junit测试的类名并右击:Go to->Generate->Test

- 之后点击Create new Test

- 之后选择Junit4,其次选择要进行测试的方法。

- 之后会看到自动生成的方法:例:
@Test public void shellSort() { }- 然后使用
assertEquals(参数一,参数二)方法,例:
@Test public void shellSort() { assertEquals(预定结果,测试的方法); //例:assertEquals("[2301, 2302, 2303, 2305, 2307, 2309]",Sorting.shellSort(list1,3));//正常 } - emmm·····,首先选中要进行Junit测试的类名并右击:Go to->Generate->Test
-
问题二:插值查找中的
mid=low+(key-a[low])/(a[high]-a[low])*(high-low)是怎么来的? -
问题而解决方案:
-
先举两个例子
- 打个比方,在英文字典里面查“apple”,你下意识翻开字典是翻前面的书页还是后面的书页呢?如果再让你查“zoo”,你又怎么查?很显然,这里你绝对不会是从中间开始查起,而是有一定目的的往前或往后翻。
- 同样的,比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5, 我们自然会考虑从数组下标较小的开始查找。
-
经过以上分析,折半查找这种查找方式,不是自适应的(也就是说是傻瓜式的)。二分查找中查找点计算如下:
mid=(low+high)/2, 即mid=low+1/2(high-low);- 通过类比,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low), - 也就是将上述的比例参数1/2改进为自适应的,也就是将1/2改进为 (key-a[low])/(a[high]-a[low])。根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
- 通过类比,我们可以将查找的点改进为如下:
收获感悟:
补博客可真是麻烦,拿起了好久都没动过的IDEA(因为最近在做实战项目)。


