1、 What is a Z-Score?
简单地说,z分数就是数据距离均值有多少个标准差。但更严格地说,它衡量的是一个数值偏离总体均值以上或以下多少个标准差。z分数也称为标准分数,可以放在正态分布曲线上。z分数范围从-3个标准差(落在正态分布曲线的最左边)到+3个标准差(落在正态分布曲线的最右边)。为了使用z分数,您还需要知道均值μ和总体标准差σ
Simply put, a z-score is the number of standard deviations from the mean a data point is. But more technically it’s a measure of how many standard deviations below or above the population mean a raw score is. A z-score is also known as a standard score and it can be placed on a normal distribution curve. Z-scores range from -3 standard deviations (which would fall to the far left of the normal distribution curve) up to +3 standard deviations (which would fall to the far right of the normal distribution curve). In order to use a z-score, you need to know the mean μ and also the population standard deviation σ.
2. Z Score Formulas
2.1 One Sample
一个样本计算z score基本公式:
z = (x – μ) / σ
例如,假设你的考试成绩是190分。测试集是一个均值(μ)150和一个标准偏差(σ)25。假设是正态分布,z分数为:
z = (x – μ) / σ= 190 – 150 / 25 = 1.6
z分数告诉你离均值有多少个标准差。在这个例子中,您的分数比平均值高1.6个标准差。
The basic z score formula for a sample is:
z = (x – μ) / σ
For example, let’s say you have a test score of 190. The test has a mean (μ) of 150 and a standard deviation (σ) of 25. Assuming a normal distribution, your z score would be:
z = (x – μ) / σ= 190 – 150 / 25 = 1.6.
The z score tells you how many standard deviations from the mean your score is. In this example, your score is 1.6 standard deviations above the mean.
您还可以看到下面显示的z分数公式。这是完全相同的公式作为z = x -μ、σ,除了x̄(样本均值)是用来代替μ(总体均值)和s(样本标准差)是用来代替σ(总体标准偏差)。然而,解决它的步骤是完全相同的。
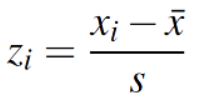
You may also see the z score formula shown to the left. This is exactly the same formula as z = x – μ / σ, except that x̄ (the sample mean) is used instead of μ (the population mean) and s (the sample standard deviation) is used instead of σ (the population standard deviation). However, the steps for solving it are exactly the same.
2.2 Standard Error of the Mean(多样本,标准误)
当你有多个样品和想要描述这些样本均值的标准差(标准误差),您将使用此z分数公式:z = (x -μ)/(σ/√n)。z分数会告诉你样本均值和总体均值之间有多少个标准差。
When you have multiple samples and want to describe the standard deviation of those sample means (the standard error), you would use this z score formula:
z = (x – μ) / (σ / √n)
This z-score will tell you how many standard errors there are between the sample mean and the population mean.
举例来说:假设,女性的平均身高是1.65,标准偏差为3.5。假设身高是正态分布,随机抽取50名平均身高70 "的女性作为样本,其概率是多少?
z = (x – μ) / (σ / √n)= (170 – 165) / (3.5/√50) = 5 / 0.495 = 10.1
In general, the mean height of women is 65″ with a standard deviation of 3.5″. What is the probability of finding a random sample of 50 women with a mean height of 70″, assuming the heights are normally distributed?
z = (x – μ) / (σ / √n)= (70 – 65) / (3.5/√50) = 5 / 0.495 = 10.
这里的关键是,我们处理的是均值的抽样分布,我们知道公式中必须包含标准误差。我们还知道,99%的值在正态概率分布中离均值的3个标准差以内。因此,任何样本女性的平均身高为170的概率都不到1% "
The key here is that we’re dealing with a sampling distribution of means, so we know we have to include the standard error in the formula. We also know that 99% of values fall within 3 standard deviations from the mean in a normal probability distribution (see 68 95 99.7 rule). Therefore, there’s less than 1% probability that any sample of women will have a mean height of 70″
2.3 从技术上讲,z分数是参考总体均值的标准差数
例如:
z分数为1比均值高1个标准差。
z分数比均值高2个标准差。
z分数比均值低1.8个标准差。
A z-score of 1 is 1 standard deviation above the mean.
A score of 2 is 2 standard deviations above the mean.
A score of -1.8 is -1.8 standard deviations below the mean
分数表示分数在正态分布曲线上的位置。z分数为0表示这些值正好是平均值,而分数为+3表示这些值比平均值高得多。
A z-score tells you where the score lies on a normal distribution curve. A z-score of zero tells you the values is exactly average while a score of +3 tells you that the value is much higher than average.



