1、Alpha Level (Significance Level,显著水平): What is it?
显著性水平α是指当零假设是正确的,但做出了错误决策的概率(即一类错误的概率)。Alpha水平(有时称为“显著性水平”)用于假设测试。通常,这些测试的alpha值为0.05(5%),但是其他常用的值是0.01和0.10。
The significance level α is the probability of making the wrong decision when the null hypothesis is true. Alpha levels (sometimes just called “significance levels”) are used in hypothesis tests. Usually, these tests are run with an alpha level of .05 (5%), but other levels commonly used are .01 and .10.
在了解之前首先看一下什么是一类错误和二类错误
2. Alpha Levels / Significance Levels: Type I and Type II errors
在假设检验中,有两种错误是可能的,第一类错误和第二类错误。
一类错误:当原假设为真时,却支持了备择假设。
二类错误:当备择假设为真时,却不支持备择假设。
In hypothesis tests, two errors are possible, Type I and Type II errors.
Type I error: Supporting the alternate hypothesis when the null hypothesis is true.
Type II error: Not supporting the alternate hypothesis when the alternate hypothesis is true
在法庭的例子中,零假设是一个人是无辜的备择假设是他有罪。如果你判定一个无辜的人有罪(第一类错误),即你支持备择假设(他有罪)。第二类错误是让罪犯逍遥法外。
In an example of a courtroom, let’s say that the null hypothesis is that a man is innocent and the alternate hypothesis is that he is guilty. if you convict an innocent man (Type I error), you support the alternate hypothesis (that he is guilty). A type II error would be letting a guilty man go free.
a级是第一类错误的概率,也就是拒绝零假设的概率。一个相关的术语,beta,是相反的;表示当替代假设为真时,拒绝它的概率。
An alpha level is the probability of a type I error, or you reject the null hypothesis when it is true. A related term, beta, is the opposite; the probability of rejecting the alternate hypothesis when it is true.
Alpha水平可以由你控制,并与自信水平相关。例如,如果你想要有95%的把握你的分析是正确的,假设你有一个单侧检验,那么alpha水平应该是1 -0.95 = 5%。对于双尾检验,将alpha值除以2,在这个例子中,两个尾部是0.05/2 = 2.5%
Alpha levels can be controlled by you and are related to confidence levels. To get α subtract your confidence level from 1. For example, if you want to be 95 percent confident that your analysis is correct, the alpha level would be 1 – .95 = 5 percent, assuming you had a one tailed test. For two-tailed tests, divide the alpha level by 2. In this example, the two tailed alpha would be .05/2 = 2.5 percent. See: One-tailed test or two? for the difference between a one-tailed test and a two-tailed test.
3. Why is an alpha level of .05 commonly used?
由于alpha级别是犯第I类错误的概率,我们将这个区域尽可能地缩小似乎是有意义的。例如,如果我们将alpha水平设置为10%,那么我们很有可能错误地拒绝零假设,而alpha水平为1%则会使面积变小。那么为什么不使用一个很小的区域而不是标准的5%呢?
Seeing as the alpha level is the probability of making a Type I error, it seems to make sense that we make this area as tiny as possible. For example, if we set the alpha level at 10% then there is large chance that we might incorrectly reject the null hypothesis, while an alpha level of 1% would make the area tiny. So why not use a tiny area instead of the standard 5%?
alpha level越小,拒绝面积越小即你拒绝零假设的概率越小。如果该区域越小,你拒绝零假设的几率越小。但当事实上你需要拒绝零假设,这时候你就犯了II类错误。也就是说你避免I类错误的几率越小,那么你犯二类错误的几率越大。科学家发现alpha level为5%是两类错误的good平衡。
The smaller the alpha level, the smaller the area where you would reject the null hypothesis. So if you have a tiny area, there’s more of a chance that you will NOT reject the null, when in fact you should. This is a Type II error.
In other words, the more you try and avoid a Type I error, the more likely a Type II error could creep in. Scientists have found that an alpha level of 5% is a good balance between these two issues.
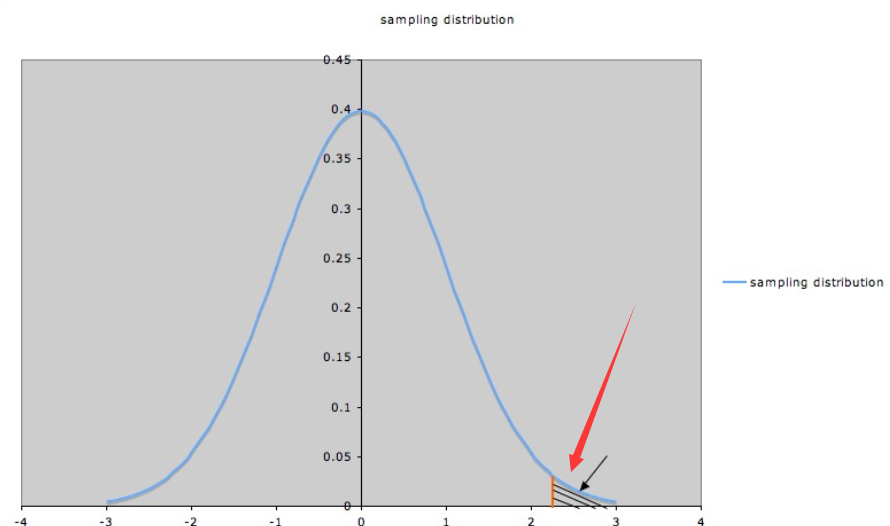
这张图显示了最右边的拒绝区域。即alpha level(即拒绝零假设的概率,或者说是犯一类错误的概率)。该区域越小,即你拒绝零假设的概率越小,越倾向于接受零假设,这样增加了II类错误的概率。



