摘要:Wright’s F‑statistics, and especially FST, provide important insights into the evolutionary processes that influence the structure of genetic variation within and among populations, and they are among the most widely used descriptive statistics in population and evolutionary genetics. Estimates of FST can identify regions of the genome that have been the target of selection, and comparisons of FST from different parts of the genome can provide insights into the demographic history of populations. For these reasons and others, FST has a central role in population and evolutionary genetics and has wide applications in fields that range from disease association mapping to forensic science. This Review clarifies how FST is defined, how it should be estimated, how it is related to similar statistics and how estimates of FST should be interpreted
例子
几乎每一种植物或动物物种都包括许多通常孤立的种群,由于遗传漂变或不同的自然选择,随着时间的推移,这些种群会发生基因分化.例如,最近基于370多个微卫星和60万个SNP的分析表明,来自主要地理区域的人口之间的遗传差异只占人类遗传多样性的5-10%。这些结果表明,地理上不同的人群之间的相似性远远大于差异性。但是,说5-10%的多样性是由人群之间的差异造成的,这意味着什么?这个数字是如何得出的?简而言之,从这些地区抽样的人群中,对微卫星数据的FST估计为0.05,对SNP估计为0.10.
历史
在20世纪40年代和50年代,SewallWright和GustaveMalecot分别独立引进F统计作为区分种群内和种群间遗传多样性划分的工具。在1931年发表的一篇论文中,Wright已经全面描述了导致种群间遗传分化的过程。群体间遗传分化量与重要进化过程(迁移、突变和漂移)的速率有可预测的关系。例如,迁移较多的大种群间差异较小,而迁移较少的小种群间差异较大,FST是这种分化的一种便利度量,因此FST和相关统计数据是群体和进化遗传学中使用最广泛的描述性统计数据之一。但是FST不仅仅是一个描述性的统计数据,更是一种遗传分化的测量。FST与群体间等位基因频率的差异直接相关,与群体内个体间的相似性程度成反比。如果FST小,说明每一个群体内的等位基因频率相似;如果值大,说明等位基因频率不同。如果在某些种群中,自然选择倾向于一个等位基因而不是另一个等位基因,那么在该位点上的FST将大于在纯粹由遗传漂变导致的群体间差异的位点上的FST。因此,将FST的单位点估计值与全基因组背景进行比较的基因组扫描,可能会识别出基因组中受到多样化影响的区域【6-8】.或者,如果群体统计学历史以不同于常染色体的遗传变异的方式影响性染色体的遗传变异,来自性染色体maker的FST的估计可能会不同与来自常染色体maker的FST的标记。进化增加了种群间的差异,也增加了种群内个体间的相似性。因此,在病例和对照之间对等位基因频率进行比对时,必须考虑FST,以确保它们之间的差异大于随机期望。
-----------------------------------------------------------------华丽丽的分割线------------------------------------------------------
1、definitions
这些参数是:FIT,个体内配子相对于整个群体的相关性;FIS,个体内配子与该个体所属亚种群的相关性;FST是指从同一亚群中随机选择的配子相对于整个亚群的相关性。
遗传多样性公式推导:
As an example of how to calculate genetic diversity, consider two populations that are segregating for two alleles at a single locus。假设第一个群体中A1等位基因的频率标记为p1,第二个群体中A1等位基因的频率为p2。A1A1基因型在第一个群体中的频率标记为x11,1;A1A2基因型被标记为x12,1;以此类推。两个群体的基因型频率由以下一组方程给出:
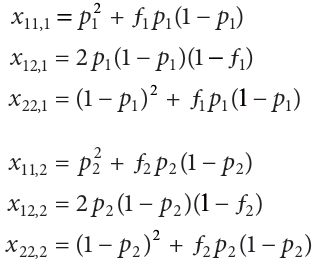
ƒ1和ƒ2通常被称为群体内近亲繁殖系数(inbreeding coefficients)。在实践中,ƒ是衡量杂合子的频率与特定基因型在哈迪温伯格定律中的预期比例(In practice, ƒ is a measure of the frequency of heterozygotes compared with that expected when genotypes are in Hardy–Weinberg proportions)。相比于哈迪温伯格定律期望值,近亲繁殖导致杂合子缺陷,所以当近亲繁殖在两个群体中都发生,ƒ1 and ƒ2 为正值。但如果个体避免近亲繁殖或存在杂合子优势,那么杂合子频率比预期的哈迪温伯格定律值更常见,ƒ1 and ƒ2 为负值。简而言之,f1和f2是衡量群体间基因型比例与哈迪温伯格定律期望值两者间的不同程度,正值表示杂合子缺陷、负值表示杂种优势等。
现在考虑一个组合sample中的基因型频率,这个组合sample由第一个群体的c%的个体和第二个群体1 - c%比例组成。类似的,基因型频率在合并后的样品中基于平均等位基因频率的实况,不等于哈迪温伯格定律期望值。等位基因频率用以下公式:
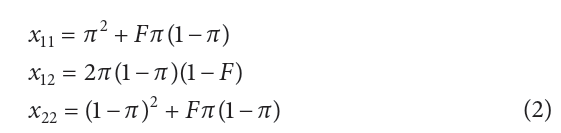
这里:
π = cp1 + (1 – c)p2 ,表示在组合 sample 中等位基因A1的平均频率
F:表示总的近交系数,其中(1 − F ) = (1 − ƒ)(1 − θ ),
其中:
ƒ = cƒ1 + (1 – c)ƒ2 ,群体间偏离温伯格的预期值的平均水平(the average within‑population departure from Hardy–Weinberg expectations)
θ: 种群间等位基因频率分化程度(a measure of allele frequency differentiation among populations).,
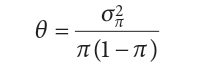
σπ2 :群体间等位基因频率的差异(is the variance in allele frequency among populations).
π(1 – π) :从整个群体中随机选择的等位基因的等位基因状态的方差(is the variance in the allelic state for an allele chosen randomly from the entire population),因此,它可以被看作是一个衡量整个种群遗传多样性的标准。
θ因此可以解释为遗传多样性的比例是由于等位基因频率的差异造成的。总之:
ƒ(FIS):个体内等位基因与其所属群体之间的相关性(correlation between alleles within individuals relative to the population to which they belong).In short, ƒ(FIS) can be thought of either as the average within‑population departure from Hardy–Weinberg expectations or as the correlation between alleles within individuals relative to the population to which they belong
θ(FST): 群体内等位基因相对于组合群体的相关性( correlation between alleles within populations relative to the combined population) ,θ(FST)can be thought of either as the proportion of genetic diversity due to allele frequency differences among populations or as the correlations between alleles within populations relative to the entire population.
F(FIT) :个体内等位基因相对于组合群体的相关性( correlation between alleles within individuals relative to the combined population)。 F(FIT) can be thought of either as the departure of genotype frequencies in the combined sample from Hardy–Weinberg expectations or as the correlation between alleles within individuals relative to the combined sample.
在Wright的表示法中,下标指的是层次结构中各层次之间的比较:IS指的是“子群体中的个体(individuals within subpopulations)”,ST指的是“总体中的子群体(subpopulations within the total population),IT指的是“总体中的个体(individuals within the total population)。
2、estimation
Statistical sampling:
对身高的估计必须考虑到从人群中抽取有限样本所带来的变化。不做这种区分类似于用人口样本计算出的平均身高的估计值来计算人口的平均身高。来自同一种群的新样本将具有不同的特征。我们将这种变异称为统计抽样。在F统计,统计抽样是指变异与从一组固定的群体中收集基因样本有关,这些群体具有固定但未知的基因型频率。通过增加组内样本的大小,可以降低与统计抽样相关的变异量。
遗传漂变导致种群间的差异,这种差异可以用这些种群间等位基因频率的分布来描述。这种分布的方差与FST直接相关(见公式2),但在典型的研究中,
只采样了一个总体子集。因此,F统计量的估计值除了要考虑与群体抽样相关的变异外,还必须考虑与等位基因频率分布的群体抽样集相关的变异。
Genetic (or evolutionary) sampling:
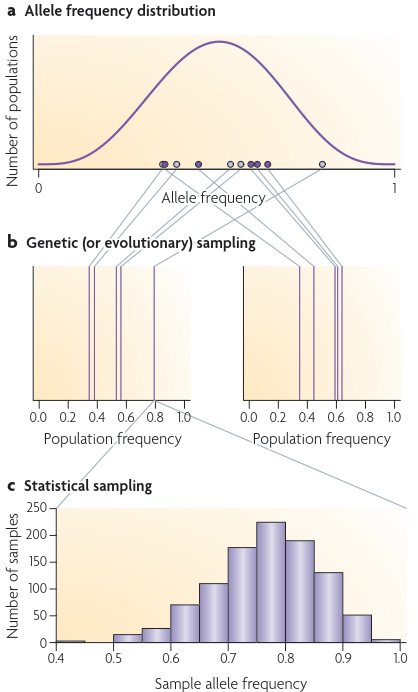
图a中显示的部分相对应的等位基因频率分布与人口平均等位基因频率的道π= 0.5和FST=θ=0.1。如果从这个分布中取样两组群体(由黑圈和光圈表示),
第一组群体(光圈)中的等位基因频率将与第二组群体(黑圈)中的等位基因频率不同。b部分提供了一个例子,在这个例子中,从a部分所示的等位基因频率分布中
随机抽取了两组不同的5个种群频率。a部分所示等位基因频率的变化反映了遗传或进化抽样的影响。b部分样本集之间的差异反映了从a部分等位基因频率分布中
抽样特定群体的影响,如果在不同的群体中重复抽样,则与实证研究中预期的结果类似。
statistical sampling:
c部分说明了更熟悉的统计抽样概念。它展示了b部分左边的群体样本中等位基因频率最大的群体样本中20个个体的1000个样本中的等位基因频率分布。
统计抽样是指从具有特定等位基因频率的群体中反复取样的等位基因所期望的样本组成的变化。研究人员可以通过增加群体内抽样的个体数量来控制与
统计抽样相关的变异数量:抽样的个体数量越大,样本等位基因频率与潜在群体频率的差异就越小。相比之下,研究人员无法控制与遗传抽样相关的变异
数量:与遗传抽样相关的变异是导致种群间分化的潜在随机进化过程的内在属性。
3、Approaches to estimating FST
3.1、moments estimates(矩估计)
矩估计方法的设计具有较低的偏差,因为如果从相同的总体中反复抽取样本,相应样本估计的平均值将接近未知的总体参数。这些同道还有另外一个优点,即它们很容易计算,而且不需要对抽取样本的分布形状做任何假设,只需要它有一个平均值和方差。于F统计,方法矩估计是基于等位基因频率的方差分析(ANOVA).方差分析是一种检验两个或两个以上群体的均值是否相等的统计方法,因此可用来评估群体之间的差异程度.如果群体内方差等于群体间方差,则没有群体亚结构。方差分析是用均方表示的。因此,在实践中,我们需要计算群体间的期望均方(即样本等位基因频率在所有群落中围绕平均等位基因频率的方差)和群体内的期望均方(即,当基因型与哈迪-温伯格比例相同时,群体内的杂合性)平均超过所有可能的样本(统计抽样),这些样本来自所有可能的具有相同进化倾向的群体(遗传抽样)。
3.2、maximum‑likelihood and Bayesian estimates
与矩法估计相比,似然估计和贝叶斯估计很难计算,而且需要确定样本的先验概率分布。一旦指定了这个概率分布,我们就可以计算一个叫做似然的量,它与给定这些参数的观测数据的概率成正比。参数的最大似然估计值是通过找出使该概率最大化的未知参数的值来获得的。在大多数情况下,最大似然估计是有偏差的。尽管如此,与相应的矩估计方法相比,它们通常具有较小的方差,且与未知总体参数的偏差较小。由于上述种种原因,极大似然法是目前应用最广泛的统计估计方法。贝叶斯估计与最大似然估计有许多相同的优点,因为它们使用相同的似然将数据与未知参数联系起来。然而,它们不同于最大似然估计,因为似然是通过在未知参数上放置先验分布来修正的,而估计是基于后验分布的,后验分布与似然和先验分布的乘积成比例。两个最大的-和可能性贝叶斯方法的缺点是估计的简单代数表达式很少有用。相反,这些估算是通过计算机计算得出的。因为用于分析贝叶斯模型的马尔可夫链蒙特卡罗方法(MCMC方法)不需要识别唯一的最大似然点,所以可以获得贝叶斯估计即使在具有数千或数万个参数的复杂模型中,对于该模型,可能性的数值最大化将是困难的或不可能的。对于F统计量,似然值指定了描述群体间等位基因频率变化的概率分布和描述群体内基因型样本的多项式分布。θ与概率分布的方差描述-群体分布的等位基因频率和基因型频率取决于等位基因频率在每个人口和ƒ.estimates得到最大化似然函数关于θ,ƒ和等位基因频率。贝叶斯方法使用相同的似然函数,ƒ放置适当的先验分布后,θ和等位基因频率、密度方法用于样本的后验分布。
3.2、Comparing the methods.
超过5000次引用,矩量法被广泛使用,部分原因是它的健壮性,部分原因是它易于实现。当种群间等位基因频率分布为正态分布时,最大似然法也给出了简单的公式,但前提是样本大小相等。贝叶斯方法允许对F统计量作出概率陈述,这些方法的扩展允许在单个模型的上下文中探索F统计量与群体统计学或环境变量之间的关系。然而,贝叶斯算法的实现方法可能需要计算时间。框3中使用了一个简单的数据集来说明从每种方法中获得的稍微不同的估计。用矩量法和贝叶斯方法对FST的估计尚未得到广泛的比较,但是我们的经验表明,当每个种群的平均个体数为中等到较大时(>20),当群体为中等到较大时(> 10-15),以及当大多数种群为多态性时,估计值的差异很小。当差异出现时,它们反映了在等位基因稀少或样本量较小时,对等位基因的频率估计处理上的差异。贝叶斯方法将等位基因的频率“平滑”到平均值,当等位基因稀少或样本量较小时,贝叶斯方法会更有侵略性。矩量法把样本的频率看作是没有平滑的固定量。文献31中的模拟结果与这个解释是一致的,尽管它们将Bayesian估计同GST32的估计数进行了比较,GST的估计数没有考虑遗传抽样。



