从算法看背包问题(1)
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。
有N件物品和一个容量为C的背包。第i件物品的重量(即体积,下同)是W[i],价值是V[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
简化一下吧,一个最大重量为5的背包,有如下物件:
| 物品 | 重量 | 价值 |
|---|---|---|
| 0 | 2 | 3 |
| 1 | 3 | 4 |
| 2 | 4 | 5 |
请问应如何选取,能使背包价值最大?
建表
在做这题之前,应该建立一个表。
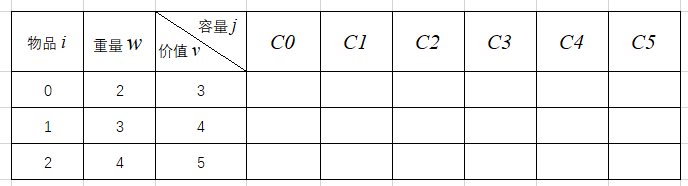
把这个表填满,就是用程序去实现算法的过程。
先决条件
令对应格子的能够存放的最大价值为$f(i,j)$,
第一条重要原则,是解决问题的先决条件
空间能给你放,你就放。
转化为数学语言就是:

第一行分析
先来看第一行,只考虑物品1:
-
考虑容量C[j],j为0,1时,物品0毫无疑问放不下。
∴ f(2,j)=0;
-
C为5时,可以放下。所以填充的价值为3.f(0,2)=v[0]=2.
-
...
第一行,要么放不下(为0,j<w[i]),要么放进去(v[i],此时j>=w[i]).
由此:
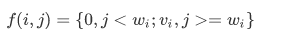
此时填充的表格为:
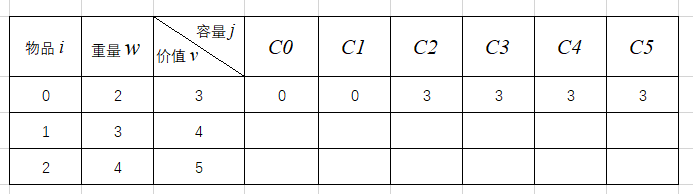
第二行分析
接着看第二行。
-
考虑容量C[j],j为0,1,2时,物品1毫无疑问放不下。f(1,j)继承f(0,j)的值。
-
j为3时,因为w[0]+w[1]>j,因此只存在个选择:要么放物品0,要么放物品1.放和不放要通过比较来决定。
如果不放物品0,那么这个值为4
如果决定物品0,那么容量此时变成了j-w[0],那么去找f(1,j-w[0])这个格子。显然f(1,j-w[0])f(1,3)0,我们要取大的那个,所以只放物品1为最优解。填入4。
-
j=5时。两个都放得下。所以f(1,5)=7
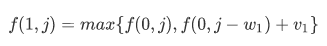
通过比较得知:此时填充的表格为:
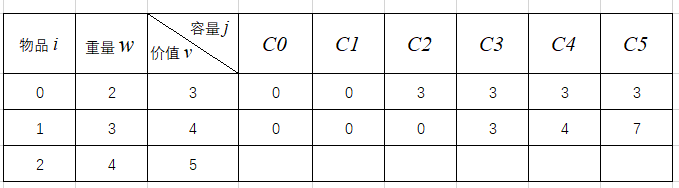
好了,背包问题的算法实际上可以结束了。
多余的第三行分析:归纳现象
为了做完整,最后再看第三行:
-
j=0,1,2,3(j<w[2])时,根本放不下物品2,不予考虑,此时:f(2,j)继承f(1,j)的值。
$f(2,j)=f(1,j)$。
-
当j=4也就是w[2]<=j时,可以放下物品2,此时需要比较
先看f(1,4),它占用了w[1]=3的空间,此时空间为j-3,找到f(2,j-3)f(2,1)0
如果直接放物品2.结果为5,因此填上5。
-
最后看C5。还是比较:f(1,5)的方案是放物品0和1,占用为2+3=5,此时空间还剩下5-5=0,去检索f(2,0)得0.
因此,取最大填上7。

算到最后,你会发现,问题的解答在于表格右下角,也就是全部的最大值。也就是7.
同时你也会发现第二第三行其实是一样的。
因此
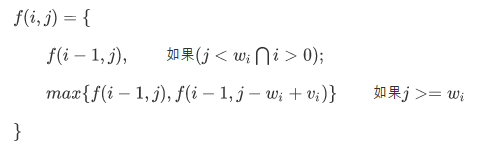
算法实现
假如后端给你的数据如下:
let table = [{
good: '鸡蛋',
weight: 2,
value: 3
}, {
good: '西红柿',
weight: 3,
value: 4
}, {
good: '茄子',
weight: 4,
value: 5
}]
还需要处理下。
class Knapsack {
constructor(table, capacity) {
// 初始化
this.nums = table.length - 1;
this.goods = [];
this.weights = [];
this.values = [];
this.capacity = capacity;
table.map((x, i) => {
this.goods.push(x.good);
this.weights.push(x.weight);
this.values.push(x.value);
});
/**
* 封装一个类,放到表格中
* items为名目
* */
this.UnitData = function () {
this.init = function (items, value) {
return {
items, value
};
}
}
}
getItems() {
// 初始化表格
let table = [[]];
let { UnitData, capacity, nums, weights, values, goods } = this;
// 创建列,第一行判断
for (let j = 0; j <= capacity; j++) {
let unitData = new UnitData();
if (j < this.weights[0]) {
// 啥也放不了
table[0][j] = unitData.init([], 0)
} else {
// 允许放第一个商品
table[0][j] = unitData.init([goods[0]], values[0])
}
}
// 第二行开始判断
for (let j = 0; j <= capacity; j++) {
for (let i = 1; i <= nums; i++) {
// 创建行
if (!table[i]) {
table[i] = [];
}
// 第2个商品起开始比较判断
if (j < weights[i]) {
// 容量小则继承
table[i][j] = table[i - 1][j];
} else {
//否则比较,查找。
let a = table[i - 1][j].value;
let b = table[i - 1][j - weights[i]].value + values[i]
if (a > b) {
table[i][j] = table[i - 1][j];
} else {
let unitData = new UnitData();
// 终于找到了。把物品扔进去!妈了个巴子的
table[i - 1][j].items.push(goods[i]);
table[i][j] = unitData.init(table[i - 1][j].items, table[i - 1][j - weights[i]].value + values[i])
}
}
}
}
// 返回表格右下角的数据
return table[nums][capacity]
}
}
var a = new Knapsack(table, 5)
console.log(a.getItems())
// { items: [ '鸡蛋', '西红柿' ], value: 7 }
由此,基于动态规划算法的0-1背包问题的问题解决。


 posted on
posted on

