数据结构第六讲: 树
第六讲 树
树是一种分层数据的抽象模型。最常见的树是家谱。(图来自网络)$h _r$

在明代世系表这棵树中,所有的皇帝都被称为节点。朱元璋称为根节点。后代是皇帝的节点,称为内部节点。没有子元素的节点比如明思宗朱由检称为外部节点或叶节点。朱棣及其后代节点称为朱元璋的子树。
以明宣宗朱瞻基为例子,他拥有三个祖先节点。因此他的深度为3。
树的高度取决于节点深度的最大值。根节点出于第0层。朱棣属于第二层。以此类推。整个世系表中,他的高度为12。
二叉树
二叉树最多只能有·2个子节点。

如:B为A的左侧子节点。E为A的右侧子节点。
二叉搜索树(BST)是一种特殊的节点。左侧子节点存放比父节点小的值。右侧子节点存放大于等于父节点的值、

功能的逐步实现
js创建一棵二叉树(BinarySearchTree),可以借鉴链表的思路
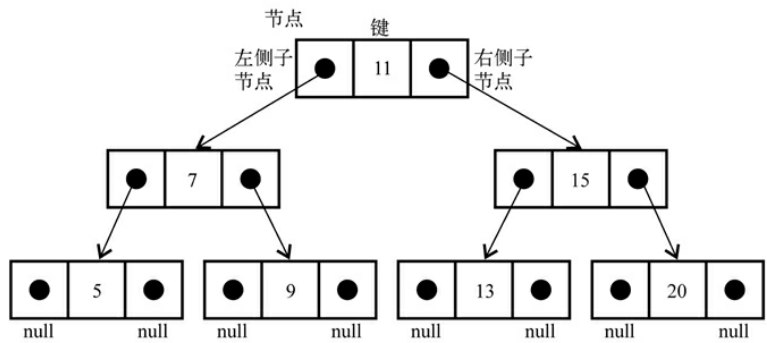
还记得链表(linkList)吗,可以通过指针来表示节点之间的关系。同时,还可以用对象来实现这个二叉树,
实现以下功能:
- insert(key):在树中插入一个新键
- search(key):在树中查找一个键,存在则返回true,否则为false
- inOderTraverse,preOderTraverse,postOderTraverse:中序/先序/后序遍历所有节点
- min/max:返回树中最小/最大的键值
- remove:从树中移除某个键。
插入节点
// 树
class BinarySearchTree{
constructor(){
this.Node=function(key){
this.key=key;
this.left=null;
this.right=null;
}
this.root=null
this.insertNode=this.insertNode.bind(this)
}
insertNode(_root,_node){
if(_root.key>_node.key){
if(_root.left==null){
_root.left=_node;
}else{
this.insertNode(_root.left,_node);
}
}else{
if(_root.right==null){
_root.right=_node;
}else{
this.insertNode(_root.right,_node)
}
}
}
// 插入
insert(key){
let Node=this.Node;
let node=new Node(key);
if(this.root==null){
this.root=node;
}else{
this.insertNode(this.root,node)
}
}
}
跑一下测试用例:
let a=new BinarySearchTree();
a.insert(11)
a.insert(7)
a.insert(15)
a.insert(5)
a.insert(3)
a.insert(9)
a.insert(8)
a.insert(10)
a.insert(13)
a.insert(12)
a.insert(14)
a.insert(20)
a.insert(18)
a.insert(25)
输出结果转化之后:
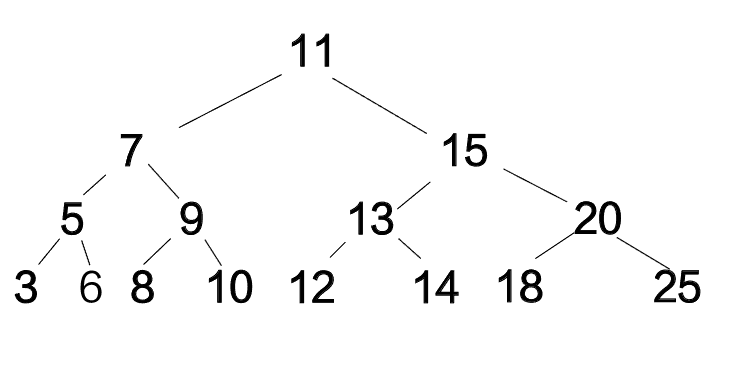
树的遍历
遍历一棵树,应当从顶层,左层还是右层开始?
遍历的方法需要以访问者模式(回调函数)体现。
树方法最常用的就是递归。那么应如何设计?
中序遍历:从最小到最大
中序遍历的顺序是“从最小到最大”。

- 每次递归前,应检查传入的节点是否为null。这是递归停止的条件。
- 调用相同的函数访问左侧子节点。直到找到最小的。
- 访问完了,再访问最近的右侧节点,直到不可访问。
// 中序遍历
inOrderTraverse(callback){
// 中序遍历所需的必要方法
const inOrderTraverseNode=(_root,_callback=()=>{})=>{
// 从顶层开始遍历
if(_root!==null){
inOrderTraverseNode(_root.left,_callback);
_callback(_root.key);
inOrderTraverseNode(_root.right,_callback);
}
}
inOrderTraverseNode(this.root,callback);
}
打印结果发现,其实这个遍历实现了树的key值从小到大排列。
a.inOrderTraverse((key)=>{console.log(key)})
// 3 5 6 7 8 9 10 11 12 13 14 15 18 20 25
先序遍历:如何打印一个结构化的数据结构
先序遍历的过程:

先把左侧子节点全部访问完了,再寻找一个距此时位置(“亲缘关系”)最近的右侧节点。
preOrderTraverse(callback){
// 中序遍历所需的必要方法
const preOrderTraverseNode=(_root,_callback=()=>{})=>{
// 从顶层开始遍历
if(_root!==null){
_callback(_root.key);
preOrderTraverseNode(_root.left,_callback);
preOrderTraverseNode(_root.right,_callback);
}
}
preOrderTraverseNode(this.root,callback);
}
所以,所谓先序遍历就是把callback的位置提前了。
后序遍历:从左到右先遍历子代

后续遍历是先访问一个树的后代节点。最后才访问本身。
那么后序遍历的方法是不是把callback放到最后执行呢?
是的。简直无脑。
// 后序遍历
postOrderTraverse(callback){
// 中序遍历所需的必要方法
const postOrderTraverseNode=(_root,_callback=()=>{})=>{
// 从顶层开始遍历
if(_root!==null){
postOrderTraverseNode(_root.left,_callback);
postOrderTraverseNode(_root.right,_callback);
_callback(_root.key);//我在后面
}
}
postOrderTraverseNode(this.root,callback);
}
搜索特定值
//是否存在
search(_key,_root){
if(!_root){
_root=this.root
}
if(!_root){
return false;
}else if(_root.key==_key){
return true;
}
if(_root.key>_key){
if(_root.left==null){
return false;
}else{
if(_root.left.key==_key){
return true
}else{
return this.search(_key,_root.left)
}
}
}else{
if(_root.right==null){
return false
}else{
if(_root.right.key==_key){
return true
}else{
return this.search(_key,_root.right)
}
}
}
}
查找最大/最小值
// 工具函数
find(_root,side){
if(!_root[side]){
return _root.key
}else{
return this.find(_root[side],side)
}
}
// 最大值,不断查找右边
max(){
return this.find(this.root,'right')
}
// 最小值
min(){
return this.find(this.root,'left')
}
会发现这是个非常轻松的事。
移除一个节点
Bst最麻烦的方法莫过于此。
-
首先,你得找到这个节点=>递归终止的条件
-
其次,判断这个节点(_root)的父节点(parentNode)和这个节点的子节点(_root.left、_root.right)判断:
- 如果
_root没有子节点,那么直接把父节点对应的side值设为null

- 如果
_root拥有一个子节点,跳过这个节点,直接把父节点的指针指向这个子节点。
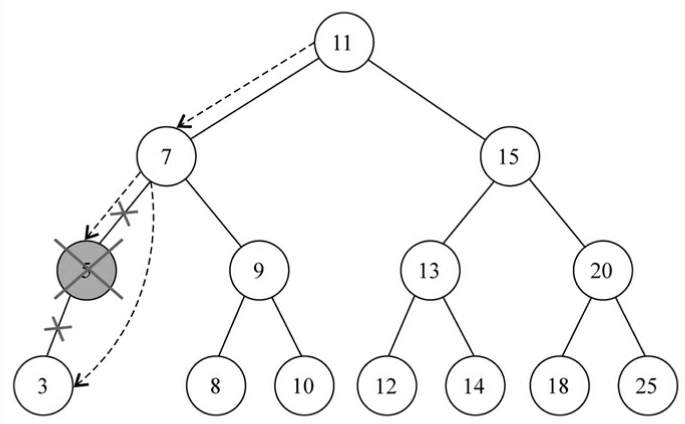
-
如果两个都有:
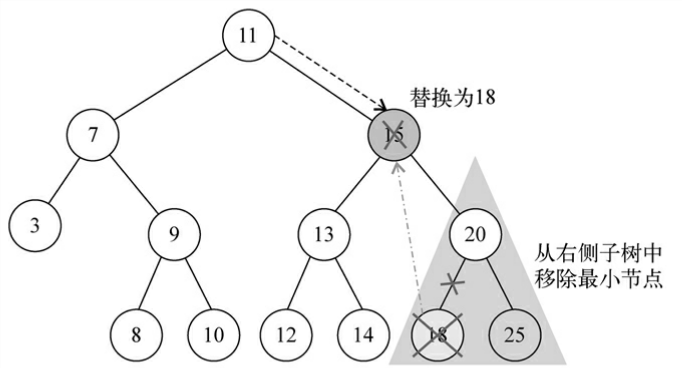
- 找到
_root右边子树的最小节点_node,然后令parentNode的指针指向这个节点 - _node的父节点删除指向_node的指针。
- 找到
- 如果
_remove(_node,_key,parentNode,side){
if(_key<_node.key){
return this._remove(_node.left,_key,_node,'left')
}else if(_key>_node.key){
return this._remove(_node.right,_key,_node,'right')
}else if(_node.key==_key){
// 顶层:移除根节点
if(!parentNode){
this.root=null;
return this.root;
}else{
if(!_node.left&&!_node.right){
// 删除的如果是叶节点
parentNode[side]=null
}else if(_node.left&&!_node.right){
let tmp=_node.left;
parentNode[side]=tmp
}else if(_node.right&&!_node.left){
let tmp=_node.right;
parentNode[side]=tmp
}else{
let tmpRight=_node.right;
// 找到右侧子树的最小节点。__node
let __node=this.find(tmpRight,'left');
// 删除这个节点。
this._remove(tmpRight,__node.key);
// 重新赋值
parentNode[side]=__node.key;
}
return this.root
}
}
}
remove(key){
if(this.search(key)){
return this._remove(this.root,key)
}else{
console.log('未找到key')
return false;
}
}
a.remove(15)
打印结果如下
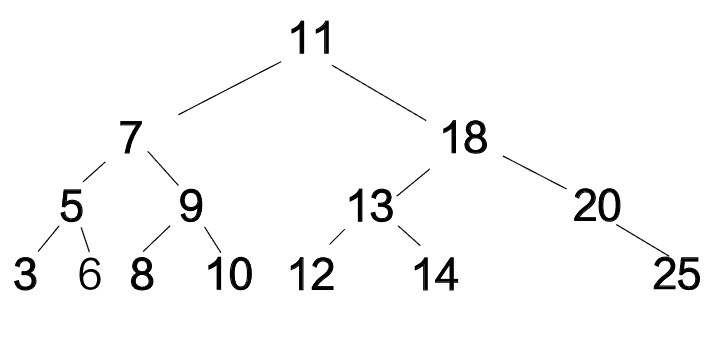
测试通过。
做一道练习
在实际工作生活中,比如一本书常分为第一讲,第1-1节,第2-1节...,第二讲:第2-1节...
如果后端发给你一个这样的数据:
let data = [{
id: '1',
children: [{
id: `1-1`,
children: [{
id: '1-1-1',
children: [{
id: '1-1-1-1'
},{
id:'1-1-1-2'
}]
},{
id:'1-1-2',
children: [{
id: '1-1-2-1'
},{
id:'1-1-2-2'
}]
}]
},{
id:'2',
children:[{
id:'2-1'
},{
id:'2-2',
children:[{
id:'2-2-1'
},{
id:'2-2-2',
children: [{
id: '2-2-2-1'
},{
id:'2-2-2-2'
}]
}]
}]
}]
}]
如何扁平化如下的json对象?
const flatJson=(_data,arr)=>{
if(!arr){
arr=[]
}
for(let i=0;i<_data.length;i++){
console.log(_data[i].id)
arr.push(_data[i].id);
if(_data[i].children){
flatJson(_data[i].children,arr)
}
}
return arr;
}
console.log(flatJson(data))
测试用例结果通过:
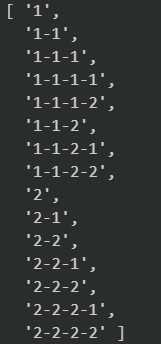
可以进一步思考:这里arr.push()在判断前执行。如果是在判断后执行,会是什么结果呢?



