霍夫变换学习

本文 OI/ACM 无关

Hough Transform

简介

Hough Transform 是图像分析，计算机视觉和数字图像处理的一种特征提取方法，它通过一种在参数空间内进行的投票机制实现分离图像内特定形状特征，经典的霍夫变换用于检测规则的曲线：直线，圆，椭圆灯，其需要以某种参数形式提供需要的特征，当无法获得特征描述时，可以使用广义霍夫变换。霍夫变换的真正优点是能容忍特征边界描述中的间隙，并且相对不受图像噪声的影响

需求性

使用边缘检测器提取边缘特征，可能因为图像数据，检测器，系统误差等方面原因，导致所需要识别的曲线上有断点或者干扰像素，将边缘特征分组到对应合适的直线，圆，椭圆等集合中式比较困难的

原理

前面我们知道图像经过边缘检测得到结果图像，在结果图像中，既包括了我们想要的边界线的像素，又包括了我们不想要的像素点；如果某一个边界线中的像素点具有一个相同的“性质”或者“特征”，那么我们就可以根据这个性质或者特征来判断图像中的像素点是否属于该边界线，我们就可以保留下我们想要的像素点，进而得到边界线。

霍夫变换判断直线边界

下列例子使用霍夫变换判断直线边界

在 \(x,y\) 坐标系 \(Z\) 下，我们有直线 \(y = mx + b\)，在该坐标系下，直线由不同的 \((x,y)|y = mx + b\) 相连得到，我们将该直线改为在参数坐标系 \(H\) 下，将 \((m,b)\) 作为坐标,该直线在参数坐标系下变成了一个点，所有在原坐标系 \(Z\) 下的过直线 \(y = mx + b\) 的点 \((x,y)\) 在 \(H\) 下都变成了经过 \((m,b)\) 点的直线

我们发现经过这样的变换，我们可以把 \(Z\) 下的点 \((x,y)\) 改写为 \(H\) 下的直线 \(b = -xm + y\)：

那么多个点变换后的多条直线，相交的交点，就是共线

img

如果我们对边缘检测图像中的每一个像素，都转换至参数坐标系下，那么在参数坐标系下，有“较多数量”直线过的点对应就是一条边界

这就是霍夫变换的思想：在参数空间内进行对点值的投票，最后通过设置阈值等方式确定出边界

但是我们发现如果使用简单的直线参数坐标空间变换，空间是无限大的，我们无法对无限大的空间内进行投票，进而我们转换向另一种直线表达方式的参数空间：Hesse normal form（即法线式）来表示直线的参数

一条直线可以表示为 \(r = x\cos\theta + y\sin\theta\)

利用参数空间 \((r,\theta)\) 解决了原本参数空间 \((m,b)\) 的空间发散问题，这个表示让霍夫变换和

二维的拉东变换非常相似。

给定一个点 \((x,y)\),利用辅助角公式可以轻松证明通过该点的所有直线集合在 \((r,\theta)\) 平面上为一三角函数。

\(r = x\cos\theta + y\sin\theta \to r = \sqrt{x^2 + y^2}(\frac{x}{\sqrt{x^2 + y^2}}\cos\theta + \frac{y}{\sqrt{x^2 + y^2}}\sin\theta) \to r = \sqrt{x^2 + y^2}\cos{(\theta - \phi)}\)

img

我们根据 \((r,\theta)\) 参数空间上的逆变化可以得到原直线：

\(y = -cot\theta x + \frac{r}{\sin\theta}\)

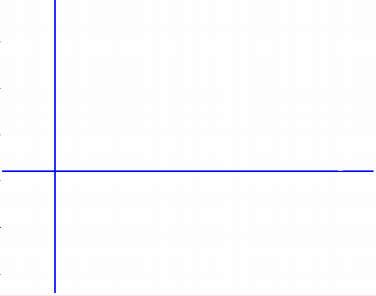
我们对参数空间进行投票后，可以通过阈值来选择特征较为明显的边界

img

img

图6

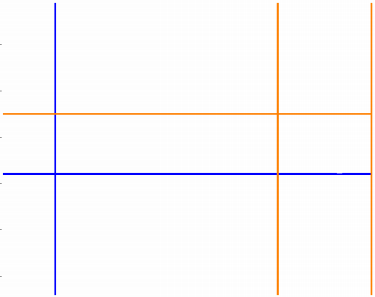
图一为原图，图二图三分别为阈值设定为 \(30/20\) 后得到的特征

霍夫变换提取圆形特征

在笛卡尔坐标系中有

\((x - a) ^ 2 + (y - b) ^ 2 = r ^ 2\)

即有

\(a = x - r\cos\theta\)

\(b = y - r\sin\theta\)

每一组 \((a,b,r)\) 是一个通过 \((x,y)\) 的圆

值得注意的是此时的 \((a,b,r)\) 在给定数据下显然是有界的，不需要额外操作

图像应该是一个倒圆锥形

Opencv在霍夫圆检测的投票并不是直接遍历每个图像上的所有点进行投票，此时参数空间上有若干三维曲线，计算开销太大，其使用的是霍夫梯度法

在计算时，先使用 Sobel算子 对边缘检测出的所有非零像素点计算了梯度，再沿着梯度方向遍历参数空间\((a,b,r)\),其提取通过梯度预估了圆心的位置。

广义霍夫变换

前文提到的用以检测直线和圆的霍夫变换都是通过解析模型，通过数学手段变换参数空间，本质是把对应的检测目标转换成交点，并统计相交数量，设计阈值统计的方法

但如果我们要检测一个非解析模型的任意形状怎么办呢

我们通过和刚刚使用的霍夫梯度法类似的方法，使用梯度方向作为特征的一维训练 R-table 来投票

image-20231117211715862

训练 R-Table

  • 选取任意一点 \(c\) 代表一待检测图形
  • 对每个边缘点计算梯度 \(\phi\) 和 指向 \(c\) 的位移向量 \(r = c - p_i\)
  • 将 \(r\) 加入以 \(\phi\) 为索引的 R-Table[\(\phi\)] 中

识别过程

image-20231117213920487

  • 对于边缘化的每一非零像素计算梯度 \(\phi\)

  • 遍历 R-Table[\(\phi\)] 中的所有向量 \(r\)

    ​ 考虑到形状放缩，我们设置一个放缩比例 \(S\)

    ​ 将 [\(x_c,y_c,S\)] 投票加1

    ​ 其中 \((x_c,y_c) = (x_i,y_i) + Sr\)

  • 统计所有的 \([x_c,y_c,S]\)，设置阈值检测是否出现形状

posted @ 2023-11-17 22:09  fhq_treap  阅读(102)  评论(0)  编辑  收藏  举报