[学习笔记\练习记录]特殊动态规划 及 动态规划的一些优化技巧
仅记录我不太熟悉 及 有待加强的类型。
因为动态规划对于题目有较强依赖性,所以结合题目一起写了。
\(dp\) 套 \(dp\)
[TJOI2018]游园会
考虑设计一个自动机处理\(LCS\)的限制。
设\(f_{i,j,k}\)为前\(i\)个字符,转移到了自动机的\(j\)节点,匹配到了\(NOI\)的第\(k\)位,即可以转移了。
那么考虑如何构建这个自动机。
\(g_{i,j}\)为第一个串匹配到\(i\),第二个串匹配到\(j\),由于第一个串是我们转移的串,转移只需知道\(g_{i - 1,x}\)和新加入的字符即可,考虑记录\(g_{i,x}\)为状态,状压其差分数组即可。
考虑每一次都是从上一层转移到下一层,我们无需直接构建该自动机,在\(dp\)时处理其即可。
[TJOI2018]游园会
#include<bits/stdc++.h>
#define ll long long
#define N 1010
#define mod 1000000007
#define popcount(S) __builtin_popcount(S)
int n,k,tot,ans[N];
char s[N];
int f[2][1 << 15][3],g[2][N];
void decode(int S) {
for (int i=1;i<=k;++i) g[0][i]=(S>>(i-1))&1;
for (int i=1;i<=k;++i) g[0][i]+=g[0][i-1];
}
int encode() {
int S=0;
for (int i=1;i<=k;++i)
if (g[1][i]-g[1][i-1]) S|=1<<(i-1);
return S;
}
void trans(int nxt,int S,int l,char c,int w) {
decode(S);
for (int i=1;i<=k;++i) {
g[1][i]=std::max(g[1][i-1],g[0][i]);
if (c==s[i]) g[1][i]=std::max(g[1][i],g[0][i-1]+1);
}
int j=encode();
f[nxt][j][l]=(f[nxt][j][l]+w)%mod;
}
int main(){
scanf("%d%d",&n,&k);
scanf("%s",s + 1);
tot = (1ll << k);
f[0][0][0] = 1;
for(int i = 0;i < n;++i){
int now = i & 1;
int nxt = 1^now;
memset(f[nxt],0,sizeof(f[nxt]));
for(int j = 0;j < tot;++j){
if(f[now][j][0]){
trans(nxt,j,1,'N',f[now][j][0]);
trans(nxt,j,0,'O',f[now][j][0]);
trans(nxt,j,0,'I',f[now][j][0]);
}
if(f[now][j][1]){
trans(nxt,j,1,'N',f[now][j][1]);
trans(nxt,j,2,'O',f[now][j][1]);
trans(nxt,j,0,'I',f[now][j][1]);
}
if(f[now][j][2]){
trans(nxt,j,1,'N',f[now][j][2]);
trans(nxt,j,0,'O',f[now][j][2]);
}
}
}
for (int i=0;i<tot;++i)
for (int j=0;j<3;++j)
ans[popcount(i)]=(ans[popcount(i)]+f[n&1][i][j])%mod;
for (int i=0;i<=k;++i) printf("%d\n",ans[i]);
}
[ZJOI2019]麻将
考虑对一副牌写作\((a_1,...a_n),(a_i \leq 4)\)的一个序列。
我们考虑如何判断一个序列是否胡了。
我们考虑建立一个胡牌自动机。
设计建自动机的\(dp\)
考虑是否能够构造一个\(dp\)。
设\(f_{0/1,i,j,k}\)记录为处理前\(i\)种牌,还有\(j\)组\((i-1,i)\),以及有\(k\)张\(i\),且存在/不存在对子时的最多面子数。
考虑可以知道\(0 \leq j,k \leq 3\)
考虑使用一个\(3 * 3\)的矩阵保留状态,单个转移时枚举用于和\((i - 2,i - 1)\)拼面子,保留若干\((i - 1,i)\)和若干张\(i\),然后剩下的牌尽可能拼面子即可。
若\(f_{1,i,x,y} > 3\)即可以胡了。
接着考虑七对子情况,我们考虑记录能拼成的对子的数目最后特批即可。
期望\(dp\)
考虑只要求出\(f(i)\)为摸了\(i\)张牌还不胡的时候的方案。
那么答案为\(1 + \frac{\sum_{i = 1}^{4n - 13}\ \ f(i)i!(4n - 13 - i)!}{(4n - 13)!}\)
考虑重设\(g_{i,j,k}\)处理为前\(i\)种牌,总共摸了\(j\)张牌,走到胡牌自动机的\(k\)号节点的方案数。
那么转移方式比较显然不再赘述。
值得注意的是其同一个大小的牌的带编号,转移时需要乘上一个选取的组合数。
[ZJOI2019]麻将
#include<bits/stdc++.h>
#define ll long long
#define N 3005
#define mod 998244353
inline ll qpow(ll a,ll b){
ll res = 1;
while(b){
if(b & 1)res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
int n,w,ans,tot,f[2][N][N],e[N][5];
ll s[N],inv[N],cnt[N];
inline ll C(int x,int y){
return s[x] * inv[y] % mod * inv[x - y] % mod;
}
struct Point{
int a[3][3];
inline void init(){
for(int i = 0;i <= 2;++i)
for(int j = 0;j <= 2;++j)
a[i][j] = -1;
}
};//矩阵
Point operator + (Point A,int b){
Point res;
res.init();
for(int i = 0;i <= 2;++i)
for(int j = 0;j <= 2;++j)
if(A.a[i][j] != -1){
for(int k = 0;k <= 2;++k){
if(b >= i + j + k){
res.a[j][k] = std::max(res.a[j][k],std::min(4,A.a[i][j] + i + (b - i - j - k) / 3));
}
}
}
return res;
}
inline void cmp(Point &A,Point b){
for(int i = 0;i <= 2;++i)
for(int j = 0;j <= 2;++j)
A.a[i][j] = std::max(A.a[i][j],b.a[i][j]);
}
//矩阵表达式
struct node{
int c;//可以组成的对子数
Point dp[2];
inline void init(){c = 0;dp[1].init();dp[0].init();}
// inline void put(){std::cout<<c<"\n";puts("");for(int op = 0;op <= 1;++op,puts(""))for(int i = 0;i <= 2;++i,puts(""))for(int j = 0;j <= 2;++j)std::cout<<dp[op].a[i][j]<<" ";puts("");}
};
inline node win(){
node res;
res.init();
res.c = -1;
return res;
}
bool operator < (node A,node B){
for(int op = 0;op <= 1;++op)
for(int i = 0;i <= 2;++i)
for(int j = 0;j <= 2;++j)
if(A.dp[op].a[i][j] != B.dp[op].a[i][j])
return A.dp[op].a[i][j] < B.dp[op].a[i][j];
return A.c < B.c;
}
using std::map;
using std::queue;
map<node,int>M;
queue<node>Q;
inline bool done(node A){
if(A.c >= 7)
return 1;
for(int i = 0;i <= 2;++i)
for(int j = 0;j <= 2;++j)
if(A.dp[1].a[i][j] >= 4)
return 1;
return 0;
}
inline node operator + (node A,int b){
if(A.c == -1)
return A;
node res;
res.init();
res.c = A.c + (b >= 2);
cmp(res.dp[0],A.dp[0] + b);
cmp(res.dp[1],A.dp[1] + b);
if(b >= 2)
cmp(res.dp[1],A.dp[0] + (b - 2));
if(done(res))
return win();
return res;
}
//自动机的一些运算
int main(){
// freopen("table2.out","w",stdout);
node root;
root.init();
root.c = 0,root.dp[0].a[0][0] = 0;
M[root] = ++ tot;
Q.push(root);
while(Q.size()){
node x = Q.front();
Q.pop();
int u = M[x];
// std::cout<<u<<std::endl;
// x.put();
for(int i = 0;i <= 4;++i){
node v = x + i;
// std::cout<<"CHOSE "<<i<<" TO "<<"\n";
// v.put();
if(M.find(v) == M.end()){
e[u][i] = M[v] = ++ tot;
Q.push(v);
if(v.c == -1)
w = tot;
}else
e[u][i] = M[v];
// std::cout<<"CHOSE "<<i<<" TO "<<e[u][i]<<"\n";
}
}
// std::cout<<tot<<std::endl;
scanf("%d",&n);
s[0] = 1;
for(int i = 1;i <= n * 4;++i)
s[i] = s[i - 1] * i % mod;
inv[n * 4] = qpow(s[n * 4],mod - 2);
for(int i = n * 4 - 1;i >= 0;--i)
inv[i] = inv[i + 1] * (i + 1) % mod;
for(int i = 1;i <= 13;++i){
int x,id;
scanf("%d%d",&x,&id);
cnt[x] ++ ;
}
f[0][0][1] = 1;//第i种,摸了k张牌,状态为j
for(int i = 1;i <= n;++i){
int now = i & 1;
int las = now ^ 1;
for(int k = 0;k <= n * 4;++k){
for(int j = 0;j <= tot;++j)
f[now][k][j] = 0;
}
for(int k = 0;k <= n * 4;++k)
for(int j = 1;j <= tot;++j)
if(f[las][k][j])
for(int t = 0;t <= 4 - cnt[i];++t){//选了多少
f[now][k + t][e[j][t + cnt[i]]] = f[now][k + t][e[j][t + cnt[i]]] + 1ll * f[las][k][j] * C(4 - cnt[i],t) % mod;
if(f[now][k + t][e[j][t + cnt[i]]] >= mod)
f[now][k + t][e[j][t + cnt[i]]] -= mod;
}
// for(int k = 0;k <= n * 4;++k,puts("")){
// for(int j = 0;j <= tot;++j)
// std::cout<<f[now][k][j]<<" ";
// }
}
for(int i = 1;i <= n * 4 - 13;++i)
for(int j = 1;j <= tot;++j){
if(j == w)continue;
ans = (ans + 1ll * f[n & 1][i][j] % mod * qpow(C(4 * n - 13,i),mod - 2) % mod) % mod;
}
std::cout<<ans + 1<<std::endl;
}
状压\(dp\)
[PKUSC2018]最大前缀和
考虑前缀最大和一定能从那个位置划分开其,其前缀最大和等于全集和,补集的前缀最大和小于\(0\)。
考虑对两个分别状压\(dp\)即可。
斜率优化\(dp\)
[NOI2014] 购票
考虑写出\(dp\).
\(f_i = \min (f_j + (d_i - d_j) * p_i + q_i)\)
其中对于\(d_i - d_j\)有\(lim_i\)限制。
考虑两个决策\(j,k\)
当\(d_j > d_k\),\(k\)决策比\(j\)决策好时:
有\(f_k + (d_i - d_k) * p_i + q_i \leq f_j + (d_i - d_j) * p_i + q_i\)
考虑化简有
\(\frac{f_k - f_j}{d_k - d_j} > p_i\),考虑维护一个下凸壳,查询时需要二分。
考虑如何处理\(lim\),有几种处理方法,一种是树剖维护单调栈,变成了\(3log\),听说可以跑过。
使用另一种方法,点分治。
考虑每次把分治重心的父亲往重心的子树处理,每次加入父亲,直到加入至顶点。
可以具体看看代码。
[NOI2014] 购票
#include<bits/stdc++.h>
#define ll long long
#define N 200005
int n,num;
int fa[N];
ll s[N],x[N],y[N],l[N];
using std::vector;
vector<int>e[N];
ll f[N];
#define inf 1e18
int tot,vis[N];
int root,siz[N],mx[N];
inline void find(int u){
siz[u] = 1;
mx[u] = 0;
for(auto v : e[u]){
if(vis[v])continue;
find(v);
siz[u] += siz[v];
mx[u] = std::max(mx[u],siz[v]);
}
mx[u] = std::max(tot - siz[u],mx[u]);
// std::cout<<"find "<<u<<" "<<siz[u]<<" "<<mx[u]<<"\n";
if(root == -1 || mx[u] < mx[root])
root = u;
return ;
}//找重心
ll d[N];
struct P{
ll x,y;
}st1[N],st2[N];
int top1,top2;
P operator - (P A,P B){return (P){A.x - B.x,A.y - B.y};}
bool operator < (P A,P B){return A.x < B.x;}
inline void dis(int u){
// std::cout<<"find "<<u<<" "<<d[u]<<"\n";
if(l[u] - d[u] >= 0)
st1[++top1] = (P){l[u] - d[u],u};
for(auto v : e[u]){
if(vis[v])continue;
d[v] = d[u] + s[v];
dis(v);
}
}
double slope(P a,P b){return (double)(1.0 * a.y - b.y) / (a.x - b.x);}
double sl[N];
inline void ins(P a){
while(top2 > 1 && slope(a,st2[top2]) <= sl[top2])
-- top2;
st2[++top2] = a;
sl[top2] = top2 > 1 ? slope(st2[top2], st2[top2 - 1]) : -1e18;
// std::cout<<"INS "<<a.x<<" "<<a.y<<" "<<top2<<std::endl;
}
#define mid ((l + r) >> 1)
inline ll qry(ll k){
int l = 1,r = top2;
ll res = 0;
ll res2 = 0;
while (l <= r) {
if (sl[mid] <= k) {
res = st2[mid].y - st2[mid].x * k, l = mid + 1;
} else
r = mid - 1;
}
return res;
}
inline void work(int u){
root = -1;
find(u);
vis[root] = 1;
int now = root;
// std::cout<<u<<" "<<now<<"\n";
if(root != u)tot = tot - siz[now],work(u);
int v = now;
ll dis2 = 0;
top1 = top2 = d[now] = 0;
dis(now);
std::sort(st1 + 1,st1 + top1 + 1);
for(int i = 1;i <= top1;++i){
ll lim = st1[i].x;
int w = st1[i].y;
// std::cout<<lim<<" "<<w<<std::endl;
while(v != fa[u] && dis2 + s[v] <= lim && fa[v])
ins((P){dis2 += s[v],f[fa[v]]}),v = fa[v];
if(top2) f[w] = std::min(f[w],qry(-x[w]) + d[w] * x[w] + y[w]);
}
for(auto v : e[now]){
if(vis[v])continue;
tot = siz[v],work(v);
}
}
int main(){
// freopen("q.in","r",stdin);
// freopen("table1.out","w",stdout);
scanf("%d%d",&n,&num);
for(int i = 2;i <= n;++i){
scanf("%d%lld%lld%lld%lld",&fa[i],&s[i],&x[i],&y[i],&l[i]);
e[fa[i]].push_back(i);
f[i] = inf;
}
tot = n,vis[0] = 1,work(1);
for(int i = 2;i <= n;++i)
std::cout<<f[i]<<"\n";
}
[SDOI2016]征途
考虑方差写作\(S^2 = \frac{\sum (x_i - \overline{x}^2)}{n} = \frac{1}{n}(\sum x_i^2 - n\overline{x}^2)\)
\(S^2m^2 =\sum x_i^2 - \overline{x}^2\)
考虑对前一部分\(dp\)。
设\(f_{i,j}\)到\(i\)划分了\(j\)段的最小\(\sum x_i^2\)。
此为经典的斜率优化问题。
[SDOI2016]征途
#include<iostream>
#include<cstdio>
#define ll long long
#define N 4000
ll n,m;
ll v[N],f[N][N],s[N];
ll head,end;
ll QWQ[N];
ll k;
inline ll a(ll x){return s[x];}
inline ll Y(ll x){return f[x][k - 1] + s[x] * s[x];}
inline ll X(ll x){return s[x];}
inline double solve(ll x,ll y){return (1.0 * Y(y) - Y(x)) / (1.0 * X(y) - X(x));}
int main(){
scanf("%lld%lld",&n,&m);
for(int i = 1;i <= n;++i)
scanf("%lld",&v[i]),s[i] = s[i - 1] + v[i];
for(int i = 1;i <= n;++i)
f[i][1] = s[i] * s[i];
for(k = 2;k <= m;++k){
head = end = 1;
QWQ[head] = 0;
for(int i = 1;i <= n;++i){
while(head < end && solve(QWQ[head],QWQ[head + 1]) < 2 * s[i]) ++ head;
f[i][k] = f[QWQ[head]][k - 1] + (s[i] - s[QWQ[head]]) * (s[i] - s[QWQ[head]]);
while(head < end && solve(QWQ[end - 1],QWQ[end]) > solve(QWQ[end],i))--end;
QWQ[++end] = i;
}
}
std::cout<<m * f[n][m] - s[n] * s[n]<<std::endl;
}
决策单调性\(dp\)
CF321E Ciel and Gondolas
由于你谷的翻译不像人话。
这里提供一个人话的翻译。
给定一个长度为 \(n\) 的序列,现在你需要将这个序列划分成连续的 \(k\) 段 被划分到同一段的两个位置\(i,j\),会产生代价 \(a_{i,j}\),不同段不会产生代价 现在请求出最小的代价。
考虑按分段数分层\(dp\)。
\(f_i = g_j + calc(i,j)\)
其中\(calc(i,j)\)是\((i,i)(j,j)\)矩形和。
考虑这类不易于写出即定柿子的二维贡献,可以想到决策单调性.
考虑是否有四边形不等式。
\(w(a,c) + w(b,d) \leq w(a,d) + w(b,c)\)
根据定义显然有。
那么有决策单调性,我们使用分治即可完成一次转移。
\(O(nklog)\)。
CF321E Ciel and Gondolas
#include<bits/stdc++.h>
#define ll long long
#define N 5005
int n,k,x;
int sum[N][N];
int f[N][N];
#define s sum
#define inf 0x3f3f3f3f
inline int clac(int x,int y){
return s[y][y] - s[y][x - 1] - s[x - 1][y] + s[x - 1][x - 1];
}
#define mid ((L + R) >> 1)
inline void dfs(int s,int L,int R,int tl,int tr){
if(L > R)return ;
f[s][mid] = inf;
int opt;
for(int i = tl;i <= std::min(tr,mid);++i){
if(f[s][mid] > f[s - 1][i - 1] + clac(i,mid)){
f[s][mid] = f[s - 1][i - 1] + clac(i,mid);
opt = i;
}
}
dfs(s,L,mid - 1,tl,opt);
dfs(s,mid + 1,R,opt,tr);
}
int main(){
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j)
scanf("%d",&x),sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + x;
for(int i = 1;i <= n;++i)
f[0][i] = inf;
for(int i = 1;i <= k;++i)
dfs(i,1,n,1,n);
std::cout<<f[k][n] / 2;
}
杂项
纯粹是不想做模拟题来摸鱼的题。
[NOI2020] 命运
自己做的时候可能口胡\(48,72\)分左右
考虑写出\(dp\)。
设\(f_{i,j}\)表示\(i\)子树内的未满足的最深的上端的限制为\(j\)的方案数。
分为两种讨论。
考虑现在的子树根节点为\(u\),处理到了\(v\),这个子树,其前缀儿子合并结果为\(g\)
那么有\(f_{u,i} = \sum_{j = 0}^{dep_u} g_{u,i} * f_{v,j}(e(u,v) = 1) + (\sum_{j = 0}^i g_{u,i}f_{v,j} + \sum_{j = 0}^{i - 1}g_{u,j}f_{v,i})(e(u,v) = 0)\)
考虑有两种做法,一种是把第二维看作离散,使用树上启发式合并来做。
另外一种是广为流传的线段树合并做法。
这里介绍第二种。
发现\(f_{u,i} = f_{u,i} * (sum_{v,dep_u} + sum_{v,i}) + f_{v,i} * sum_{x,i - 1}\)
其可以使用线段树合并操作。
点击查看代码
//晦暗的宇宙,我们找不到光,看不见尽头,但我们永远都不会被黑色打倒。——Quinn葵因
#include<bits/stdc++.h>
#define ll long long
#define N 1000050
int n,m;
using std::vector;
vector<int>A[N];
vector<int>V[N];
int dep[N];
int head[N];
struct P{
int l,r;
ll sum,mul;
}T[N * 10];
#define mul(x) T[x].mul
#define sum(x) T[x].sum
#define ls(x) T[x].l
#define rs(x) T[x].r
#define mid ((l + r) >> 1)
#define mod 998244353
inline void down(int p){
if (ls(p)) {
sum(ls(p)) = sum(ls(p)) * mul(p) % mod;
mul(ls(p)) = mul(ls(p)) * mul(p) % mod;
}
if (rs(p)) {
sum(rs(p)) = sum(rs(p)) * mul(p) % mod;
mul(rs(p)) = mul(rs(p)) * mul(p) % mod;
}
mul(p) = 1;
}
inline ll query(int u,int l,int r,int p){
if(!u || r <= p)return sum(u);
ll res = 0;
down(u);
res = res + query(ls(u),l,mid,p);
if(p > mid)
res = res + query(rs(u),mid + 1,r,p);
return res;
}
int cnt;
inline void change(int &u,int l,int r,int p){
if(!u)u = ++cnt;
sum(u) = mul(u) = 1;
if(l == r)return ;
if(p <= mid)
change(ls(u),l,mid,p);
else
change(rs(u),mid + 1,r,p);
}
inline int merge(int x,int y,int l,int r,ll &s1,ll &s2){
if(!x || !y){
if(!x){
(s1 += sum(y)) %= mod;
mul(y) = mul(y) * s2 % mod;
sum(y) = sum(y) * s2 % mod;
return y;
}else{
(s2 += sum(x)) %= mod;
mul(x) = mul(x) * s1 % mod;
sum(x) = sum(x) * s1 % mod;
return x;
}
}
if(l == r){
ll tx = sum(x),ty = sum(y);
s1 = (s1 + ty) % mod;
sum(x) = (sum(x) * s1 + sum(y) * s2) % mod;
s2 = (s2 + tx) % mod;
return x;
}
down(x),down(y);
ls(x) = merge(ls(x),ls(y),l,mid,s1,s2);
rs(x) = merge(rs(x),rs(y),mid + 1,r,s1,s2);
sum(x) = (sum(ls(x)) + sum(rs(x))) % mod;
return x;
}
inline void dfs(int u,int fa){
dep[u] = dep[fa] + 1;
int mx = 0;
for(auto v : V[u])mx = std::max(mx,dep[v]);
change(head[u],0,n,mx);
for(auto v : A[u]){
if(v == fa)continue;
dfs(v,u);
ll S = query(head[v],0,n,dep[u]),SS = 0;
head[u] = merge(head[u],head[v],0,n,S,SS);
}
}
int main(){
scanf("%d",&n);
for(int i = 1;i < n;++i){
int x,y;
scanf("%d%d",&x,&y);
A[x].push_back(y);
A[y].push_back(x);
}
scanf("%d",&m);
for(int i = 1;i <= m;++i){
int x,y;
scanf("%d%d",&x,&y);
V[y].push_back(x);
}
dfs(1,0);
std::cout<<query(head[1],0,n,0)<<"\n";
}
[APIO2016]烟火表演
考虑设\(f_i(x)\)为\(x\)的子树内到\(x\)的路径均为\(i\)的代价,归纳法知其为一个下凸壳。
考虑把下凸壳向父亲更新。
那么有\(g_i(x)\)为向父亲贡献的代价,考虑如何从\(f_i(x)\)转为\(g_i(x)\)即多加\((u,v)\)的边。
考虑如何转换。
设\((u,v) = l,u\ is\ fa_v\)
设下凸壳的斜率为\(0\)的区间为\([L,R]\)
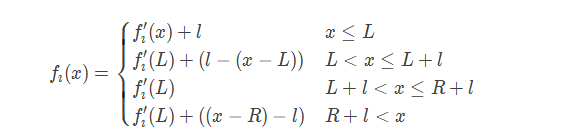
以上\(f_i(x) = g_i(x),f'_i(x) = f_i(x)\),LaTex太难打了。
考虑这四种操作的实质。
实际上是把\(<L\)的向上平移\(l\),\([L,R]\)向右平移\(l\),中间插入一条斜率\(-1\)的直线,右侧改成斜率为\(1\)的直线。
那么直接使用可并堆维护斜率转点即可。
[PKUWC2018]Minimax
可能遇到这种值域上dp的东西就是需要暴力一点啊。
直接设\(f_{i,j}\)为概率。
考虑双儿子向父亲转移:
\(F_j = f_{l,j} * (p_i \sum_{k = 1} ^{j - 1} f_{r,k} + (1 - p_i)\sum_{k = j + 1} ^ m f_{r,k}) + f_{r,j} * (p_i \sum_{k = 1} ^{j - 1} f_{l,k} + (1 - p_i)\sum_{k = j + 1} ^ m f_{l,k})\)
这个可以直接使用线段树合并时顺带维护前缀后缀和即可。
点击查看代码
#include <cstdio>
#include <algorithm>
int read() {
int x = 0;
char c = 0;
while (c < 48) c = getchar();
while (c > 47) x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return x;
}
const int mod = 998244353;
int qpow(int x, int y) {
int ans = 1;
for (; y; y >>= 1, x = 1ll * x * x % mod)
if (y & 1) ans = 1ll * ans * x % mod;
return ans;
}
int n;
const int maxn = 3e5 + 10;
int ch[maxn][2], fa[maxn], cnt[maxn], val[maxn], tmp[maxn], qwq = 0, s[maxn];
int rt[maxn], ls[maxn << 5], rs[maxn << 5], sum[maxn << 5], mul[maxn << 5];
int ans = 0, tot = 0;
void pushup(int rt) { sum[rt] = (sum[ls[rt]] +sum[rs[rt]]) % mod; }
void pushmul(int rt, int v) {
if (!rt) return;
sum[rt] = 1ll * sum[rt] * v % mod;
mul[rt] = 1ll * mul[rt] * v % mod;
}
void pushd(int rt) {
if (mul[rt] == 1) return;
if (ls[rt]) pushmul(ls[rt], mul[rt]);
if (rs[rt]) pushmul(rs[rt], mul[rt]);
mul[rt] = 1;
}
int newnode() {
int x = ++ tot;
ls[x] = rs[x] = sum[x] = 0, mul[x] = 1 ;
return x ;
}
void upd(int& p, int l, int r, int x, int v) {
if (!p) p = newnode() ;
if (l == r) {
sum[p] = v;
return;
}
pushd(p);
int mid = l + r >> 1;
(x <= mid) ? upd(ls[p], l, mid, x, v) : upd(rs[p], mid + 1, r, x, v);
pushup(p);
}
int merge(int x, int y, int l, int r, int xmul, int ymul, int v) {
if (!x && !y) return 0;
if (!x) {
pushmul(y, ymul);
return y;
}
if (!y) {
pushmul(x, xmul);
return x;
}
pushd(x), pushd(y);
int mid = l + r >> 1;
int lsx = sum[ls[x]], lsy = sum[ls[y]], rsx = sum[rs[x]], rsy = sum[rs[y]];
ls[x] = merge(ls[x], ls[y], l, mid, (xmul + 1ll * rsy % mod * (1 - v + mod)) % mod,
(ymul + 1ll * rsx % mod * (1 - v + mod)) % mod, v);
rs[x] = merge(rs[x], rs[y], mid + 1, r, (xmul + 1ll * lsy % mod * v) % mod,
(ymul + 1ll * lsx % mod * v) % mod, v);
pushup(x);
return x;
}
void out(int x, int l, int r) {
if (!x) return;
if (l == r) {
s[l] = sum[x];
return;
}
int mid = l + r >> 1;
pushd(x);
out(ls[x], l, mid);
out(rs[x], mid + 1, r);
}
void dfs(int u) {
if (!cnt[u]) upd(rt[u], 1, qwq, val[u], 1);
if (cnt[u] == 1) dfs(ch[u][0]), rt[u] = rt[ch[u][0]] ;
if (cnt[u] == 2) dfs(ch[u][0]), dfs(ch[u][1]), rt[u] = merge(rt[ch[u][0]], rt[ch[u][1]] ,1 , qwq , 0 , 0 , val[u]);
}
int main() {
n = read();
for (int i = 1; i <= n; i++) fa[i] = read();
for (int i = 1; i <= n; i++)
if (fa[i]) ch[fa[i]][cnt[fa[i]]++] = i;
for (int i = 1; i <= n; i++) val[i] = read();
for (int i = 1; i <= n; i++) {
if (cnt[i]) {
val[i] = 1ll * val[i] * qpow(10000, mod - 2) % mod;
} else {
tmp[++qwq] = val[i];
}
}
std ::sort(tmp + 1, tmp + qwq + 1);
for (int i = 1; i <= n; i++)
if (!cnt[i]) val[i] = std ::lower_bound(tmp + 1, tmp + qwq + 1, val[i]) - tmp;
dfs(1);
out(rt[1], 1, qwq);
for (int i = 1; i <= qwq; i++) ans = (ans + 1ll * i * tmp[i] % mod * s[i] % mod * s[i]) % mod;
printf("%d\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号