[学习笔记]《基于连通性状态压缩的动态规划问题》阅读笔记

给一个\(m*n\)的棋盘，有的格子是障碍，求问有多少条回路使得经过每个非障碍格子恰好一次。\(m,n \leq 12\)。

这是基于棋盘模型的问题。

有三种划分阶段：逐行，逐列，逐格。

对本题来说行列的递推方式的影响并不大。

插头

我们先引入一个重要的概念“插头”，对于一个四联通的问题来说，他通常有上下左右四个插头，一个方向的插头存在表示这个格子在这个方向可以于外面相连，这题要求回路个数，发现四个插头恰好有两个插头被拼接，有6种情况。

逐行递推：

我们不妨按从上到下的顺序考虑每行，分析第\(i\)行到\(i+1\)行有影响。

我们需要的是第\(i\)行的每个格子是否有下插头，这决定了第\(i + 1\)行是否有上插头，但仅仅记录插头是不够的，我们为了防止出现多个回路的情况，我们还需要记录第\(i\)行的\(n\)个格子的联通情况。

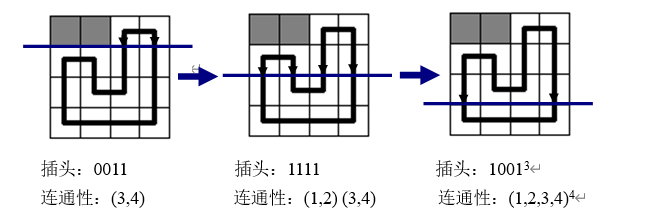
我们称图中的蓝线叫做轮廓线，任何时候只有轮廓线上方与其直接相连的格子和插头才会对轮廓线以下的格子产生直接的影响。

考虑\(f(i,S_0,S_1)\),为\(i\)行，第\(i\)行的\(n\)个格子是否具有下插头的一个\(n\)位的二进制数为\(S_0\),第\(i\)行的\(n\)个格子之间的连通性为\(S_1\)的方案总数。

如何表示\(n\)个格子的连通性呢，采用联通板块编号最小表示法。

状态表示的优化

发现如果某个格子没有下插头，那么它就不会再与轮廓线以下的格子直接相连，它的连通性对轮廓以下的部分的连通性是没有用的，所以我们直接把有向下的插头写做其所在的编号。

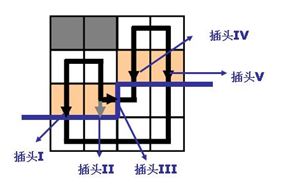
逐格递推

考虑记录状态从上一行记录转为记录划分分界点，前者记录这行前面已确定的点，后者记录上一行的点。

（后续待更新）