[学习笔记]最大权闭合子图
定义
一个有向图,有点权\(w_i\),对于子图为闭合的最大权和。
解法
先给定一个解法
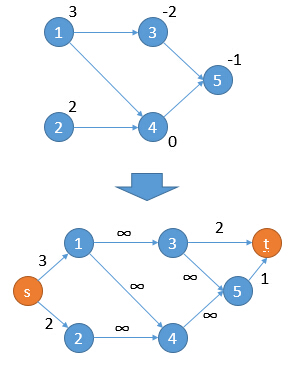
对
\(w_i > 0\),连\((S,i,w_i)\)
\(w_i < 0\),连\((i,T,-w_i)\)
原图边连
\((u,v,\infty)\)
答案为所有正点权之和 - 最小割。
证明:
- 知最小割一定为简单割
- 知简单割和闭合子图对应
那么最大权闭合子图的权的
闭合子图和\(S\)构成集合\(V_s\),其余点和\(T\)构成\(V_T\)
\(W = V_{s1} - V_{s2}
\\s1 = \forall i \in s,w_i > 0\\s2 = \forall i \in s,w_i < 0
\\V_k = sum_{i \in k}|w_k|\)
最小割\(c(S,T) = V_{T1} + V_{S2}\)
所以\(W + c(s,t) =\)所有正点权和



