[学习笔记]支配树

支配树（DominatorTree）

对于一个流程图,单源有向图，上点$w$，如果去掉一个点$d$,使得源点无法到达则称其支配$w$。

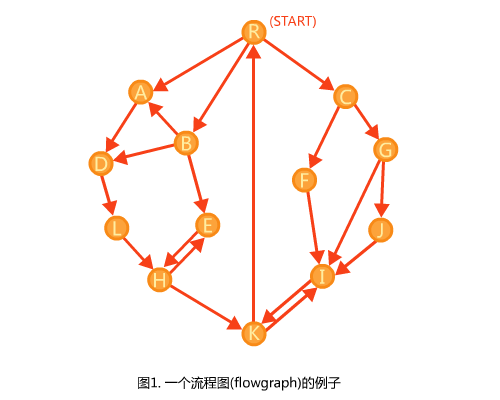
通过定义，我们知道支配的这个定义，满足传递性。

定理一：

除源点外所有点均有单一的最近支配点。

且我们知道如果我们找到最近的支配点$(immediatedominator)$,$idom(w)$，以源点作为祖先，将其构成树，则满足一个点的祖先链上全为其的支配点。

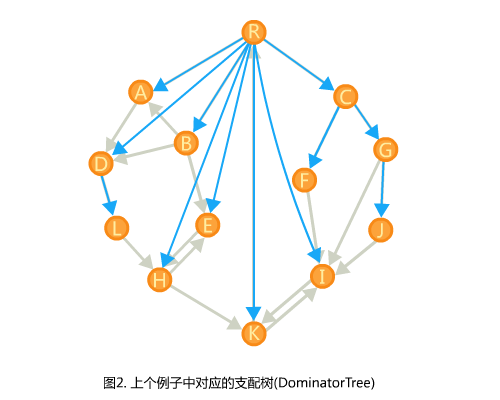
支配树相关性质：

我们随便选择一颗生成树。

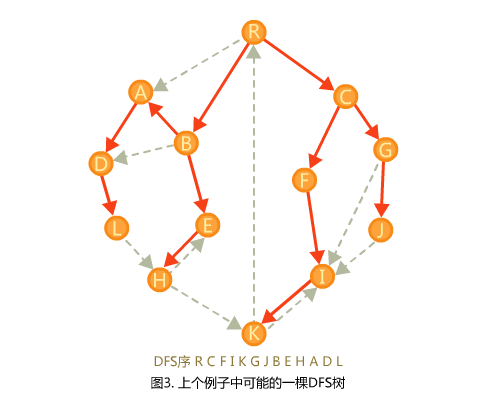
下列的所有比较均为$dfn$序比较。

引理一：路径原理：
如果两个点满足$v\le w$，那么所有$v$到$w$的路径经过其公共祖先。

符号规定

下列规定一些符号：

$a\to b$代表点$a$直接经过一条边到达点$b$

$a⇝b$代表点$a$经过某条路径到达点$b$

$a\stackrel{。}{\to }b$代表经过DFS树到达点$b$。

$a\stackrel{+}{\to }b$代表$a\stackrel{。}{\to }b$且$a\ne b$

定义半支配点

对于$w\ne r$，他的半支配点$(semi-dominator)$定义为$sdom(w)=minv|\mathrm{\exists }(v_0,v+1,...v_{k-1},v_k),v_0=v,v_k=w,\mathrm{\forall }(i\ne 0)v_i>w$

引理2:对于任意$w\ne r$，有$idom(w)\stackrel{+}{\to }w$

引理3:对于任意$w\ne r$，有$sdom(w)\stackrel{+}{\to }w$

引理4：对于任意$w\ne r$，有$idom(w)\stackrel{。}{\to }sdom(w)$
证明：考虑若不如此，则存在一条$r\stackrel{。}{\to }sdom(w)⇝w$,与$idom$定义矛盾。

引理5:对于满足$v\stackrel{。}{\to }w$,$v\stackrel{。}{\to }idom(w)$或$idom(w)\stackrel{。}{\to }idom(v)$
证明：如果不是这样：该情况为:$idom(v)\stackrel{+}{\to }idom(w)\stackrel{+}{\to }v\stackrel{+}{\to }w$,那么存在路径$r\stackrel{。}{\to }idom(v)⇝v\stackrel{+}{\to }w$,不经过$idom(w)$到达了$w$，因为$idom(w)$为$idom(v)$的真后代，一定不支配$v$

前面几条引理较为简单。

后面我们来证明一些较为复杂的定理。

定理二：

定理三：

推论一：

接下里考虑如何快速求出$sdom$

定理四：

Lengauer-Tarjan算法

算法有四步：
一：先跑出$DFS$
二：利用定理四从大到小求出$sdom$
三：通过推论一求出所有能确定的$idom$，否则记录和哪个点的$idom$相同
四：从小到大跑出所有的点的$idom$

细节：

支配树

#include<bits/stdc++.h>
#define ll long long 
#define N 200005

using std::vector;

int n,m;

vector<int>to[N];
vector<int>in[N];
vector<int>buk[N];
int head[N];

int sdom[N],idom[N];

int fa[N];
int eval[N];

//DSU

int dfn[N],cnt;
int inv[N];
int F[N];
int vis[N];
//tree 

inline void dfs(int u){
	vis[u] = 1;
	dfn[u] = ++cnt;
	sdom[u] = dfn[u];
	inv[dfn[u]] = u;
	for(int i = 0;i < to[u].size();++i){
		if(!vis[to[u][i]]){
			int v = to[u][i];
			F[v] = u;
			dfs(v);
		}
	}
}

//sdom : dfn eval : point idom : point

inline int find(int u){
	if(fa[u] == u)return u;
	int f = find(fa[u]);
	if(sdom[eval[fa[u]]] < sdom[eval[u]])
	eval[u] = eval[fa[u]];
	return fa[u] = f; 
}

inline void merge(int x,int y){//x -> y
//	std::cout<<"("<<x<<"->"<<y<<")"<<std::endl;
	fa[x] = y;
}

inline void delta(int u){
	for(;head[u] < buk[u].size();++head[u]){
		int v = buk[u][head[u]];
		int f = find(v);
		if(sdom[eval[v]] == sdom[v])
		idom[v] = u;
		else
		idom[v] = eval[v];
	}
}

inline void del(int u){
	for(int i = 0;i < in[u].size();++i){
		int v = in[u][i];
		int f = find(v);
		sdom[u] = std::min(sdom[u],sdom[eval[v]]);
	}
	buk[inv[sdom[u]]].push_back(u);
	merge(u,F[u]);
	delta(F[u]);
}

//Dom tree

vector<int>A[N];

int siz[N];

inline void serch(int u){
	siz[u] = 1;
	for(int i = 0;i < A[u].size();++i)
	serch(A[u][i]),siz[u] += siz[A[u][i]];
}

int s;

int main(){
	scanf("%d%d%d",&n,&m,&s);
	for(int i = 1;i <= n;++i)
	fa[i] = i,eval[i] = i;
	for(int i = 1;i <= m;++i){
		int x,y;
		scanf("%d%d",&x,&y);
		x ++ ,y ++ ;		
		to[x].push_back(y);
		in[y].push_back(x);
	}
	dfs(s + 1);
	for(int i = n;i >= 2;--i){
		int u = inv[i];
		del(u);//find_sdom
	}
	for(int i = 1;i <= n;++i){
		int u = inv[i];
		if(idom[u] != inv[sdom[u]])
		idom[u] = idom[idom[u]];
	}
	for(int i = 1;i <= n;++i)
	std::cout<<idom[i]<<" ";
}