[练习记录]优化基础技巧
二分系列
对于凸函数的二分
略。
分数规划
[USACO18OPEN]Talent Show G
这类带限制的分数规划直接按其限制\(dp\)即可。
[USACO18OPEN]Talent Show G
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define ll long long
#define N 255
#define M 1005
int n;
int w[N],t[N];
int W;
struct P{
int wi;
double key;
}e[N];
bool operator < (P a,P b){
return a.key > b.key;
}
double f[N][M];
inline bool check(double mid){
for(int i = 1;i <= n;++i)
e[i].wi = w[i],e[i].key = 1.0 * t[i] - mid * w[i];
std::sort(e + 1,e + n + 1);
int noww = 0;
double nowt = 0;
int k = 0;
for(int i = 1;i <= n;++i)
if(e[i].key > 0){
noww += e[i].wi;
nowt += e[i].key;
}else{
k = i;
break;
}
// std::cout<<mid<<std::endl;
// std::cout<<noww<<" "<<nowt<<std::endl;
if(noww >= W)
return 1;
std::memset(f,-0x7f,sizeof(f));
f[k - 1][0] = 0;
for(int i = k;i <= n;++i)
for(int j = 1;j <= W;++j){
f[i][j] = f[i - 1][j];
f[i][j] = std::max(f[i][j],f[i - 1][std::max(0,j - e[i].wi)] + e[i].key);
}
for(int j = W - 1;j >= 1;--j)
f[n][j] = std::max(f[n][j],f[n][j + 1]);
// std::cout<<mid<<std::endl;
// std::cout<<noww<<" "<<nowt<<" "<<std::endl;
return (f[n][W - noww] + nowt) >= 0;
}
int main(){
scanf("%d%d",&n,&W);
for(int i = 1;i <= n;++i)
scanf("%d%d",&w[i],&t[i]);
double l = 0.0,r = 1000.0;
double ans = 0;
#define mid ((l + r) * .5)
for(int i = 1;i <= 500;++i){
if(check(mid))
ans = mid,l = mid;
else
r = mid;
}
// std::cout<<check(1.06)<<std::endl;
std::cout<<(int)(1000 * ans)<<std::endl;
}
[JSOI2016]最佳团体
树上\(dp\)处理检查。
[JSOI2016]最佳团体
#include<algorithm>
#include<cstdio>
#define FIO "team"
using namespace std;
int n,k,tot,s[2510],p[2510],r[2510],head[2510],nxt[2510],to[2510],size[2510];
double L,R=3.0,mid,eps=1e-5,f[2510][2510],F[2510];
void add(int x)
{
nxt[++tot]=head[r[x]],head[r[x]]=tot,to[tot]=x;
}
void dfs(int x)
{
size[x]=1,f[x][1]=p[x]-s[x]*mid;
for(int i=head[x];i;i=nxt[i]){
dfs(to[i]);
for(int j=1;j<=size[x]+size[to[i]];j++) F[j]=-1e9;
for(int j=1;j<=size[x];j++) for(int k=0;k<=size[to[i]];k++) F[j+k]=max(F[j+k],f[x][j]+f[to[i]][k]);
for(int j=1;j<=size[x]+size[to[i]];j++) f[x][j]=F[j];
size[x]+=size[to[i]];
}
}
int pd()
{
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) f[i][j]=-1e9;
dfs(0);
return f[0][k+1]<=0;
}
int main()
{
//freopen(FIO".in","r",stdin);
//freopen(FIO".out","w",stdout);
scanf("%d%d",&k,&n);
for(int i=1;i<=n;i++) scanf("%d%d%d",&s[i],&p[i],&r[i]),add(i);
while(L+eps<R){
mid=(L+R)/2.0;
if(pd()) R=mid;
else L=mid+eps;
}
printf("%.3lf",L);
}
[SDOI2017]新生舞会
发现我们二分之后。
变成了选取\(n\)对不交集合,权值最大。
费用流经典问题,要注意的是实数二分不用跑太多次,不然会喜提和暴力哥一样的成绩。
[SDOI2017]新生舞会
#include<bits/stdc++.h>
#define ll long long
#define N 210
int a[N][N];
int b[N][N];
int n;
struct P{
int to,next,v;
double c;
}e[N * N * 2];
int s,t;
int cnt = 1,head[N << 1];
inline void add(int x,int y,int v,double c){
e[++cnt].to = y;
e[cnt].next = head[x];
e[cnt].v = v;
e[cnt].c = c;
head[x] = cnt;
}
bool vis[N];
double minc[N];
int minv[N],pre[N];
std::queue<int>QWQ;
inline bool spfa(){
for(int i = 1;i <= (n << 1) + 2;++i)
minc[i] = minv[i] = 0x3f3f3f3f,vis[i] = 0,pre[i] = 0;
QWQ.push(s);
vis[s] = 1;
minc[s] = 0;
while(!QWQ.empty()){
int u = QWQ.front();
// std::cout<<u<<" "<<pre[u]<<" "<<e[pre[u] ^ 1].to<<std::endl;
QWQ.pop();
vis[u] = 0;
for(int i = head[u];i;i = e[i].next){
ll v = e[i].to;
// std::cout<<"->"<<v<<std::endl;
if(e[i].v && minc[v] > minc[u] + e[i].c){
minv[v] = std::min(minv[u],e[i].v);
minc[v] = minc[u] + e[i].c;
pre[v] = i;
if(!vis[v])
vis[v] = 1,QWQ.push(v);
}
}
}
return minc[t] != 0x3f3f3f3f;
}
int ansv;
double ansc;
inline void EK(){
ansv = 0;
ansc = 0;
while(spfa()){
ansv += minv[t];
ansc += minc[t] * minv[t];
int now = t;
while(now != s){
e[pre[now]].v -= minv[t];
e[pre[now] ^ 1].v += minv[t];
now = e[pre[now] ^ 1].to;
}
}
}
inline bool check(double mid){
cnt = 1;
for(int i = 1;i <= (n << 1) + 10;++i)
head[i] = 0;
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j){
double k = a[i][j] * 1.0 - b[i][j] * mid;
add(i,j + n,1,-k);
add(j + n,i,0,k);
}
for(int i = 1;i <= n;++i)
add(s,i,1,0),add(i,s,0,0);
for(int i = n + 1;i <= n << 1;++i)
add(i,t,1,0),add(t,i,0,0);
EK();
return ansc <= 0;
}
int main(){
scanf("%d",&n);
s = n * 2 + 1;
t = n * 2 + 2;
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j)
scanf("%d",&a[i][j]);
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j)
scanf("%d",&b[i][j]);
double l = 0.0,r = 1e6;
double ans = 0;
#define mid ((l + r) * .5)
for(int i = 1;i <= 80;++i){
// std::cout<<l<<" "<<r<<std::endl;
if(check(mid))
ans = mid,l = mid;
else
r = mid;
}
printf("%.6f",ans);
}
凸优化
CF739E Gosha is hunting
被卡精度了./fn
考虑我们先做一个硬的三维\(f_{i,j,k}\)其转移显然。
此时我们可以发现固定后两维的一维,其对另一维是下凸函数,然后我们优化一维为凸优化,复杂度\(O(n^2log)\)
CF739E Gosha is hunting
#include<bits/stdc++.h>
#define ll long long
#define N 2005
int n,a,b;
double p[N],q[N];
struct P{double exp;int cnt;P(){exp = cnt = 0;}};//期望,使用第一种求的数量。
P f[N][N];
inline P cmax(P a,P b){
return a.exp < b.exp ? b : a;
}
inline void check(double mid){
for(int i = 1;i <= n;++i)
for(int j = 0;j <= std::min(i,b);++j){
f[i][j].exp = 0;
f[i][j].cnt = 0;
f[i][j] = f[i - 1][j];
P to;//转移
if(j > 0){
to.exp = f[i - 1][j - 1].exp + q[i],to.cnt = f[i - 1][j - 1].cnt;
// std::cout<<"case2 "<<to.exp<<" "<<to.cnt<<std::endl;
f[i][j] = cmax(f[i][j],to);
to.exp = f[i - 1][j - 1].exp + q[i] + p[i] - mid - p[i] * q[i],to.cnt = f[i - 1][j - 1].cnt + 1;
// std::cout<<"case3 "<<to.exp<<" "<<to.cnt<<std::endl;
f[i][j] = cmax(f[i][j],to);
}
to.exp = f[i - 1][j].exp + p[i] - mid,to.cnt = f[i - 1][j].cnt + 1;
// std::cout<<"case1 "<<to.exp<<" "<<to.cnt<<std::endl;
f[i][j] = cmax(f[i][j],to);
// std::cout<<i<<" "<<j<<" "<<f[i][j].exp<<" "<<f[i][j].cnt<<std::endl;
}
}
int main(){
scanf("%d%d%d",&n,&a,&b);
for(int i = 1;i <= n;++i)
scanf("%lf",&p[i]);
for(int i = 1;i <= n;++i)
scanf("%lf",&q[i]);
// for(int i = 1;i <= n;++i)
// std::cout<<p[i]<<" "<<q[i]<<std::endl;
double l = 0.0,r = 1;
#define mid ((l + r) * .5)
// check(0.375);
double fans = 0;
for(int i = 1;i <= 200;++i){
// std::cout<<l<<" "<<r<<std::endl;
check(mid);
// std::cout<<"!"<<mid<<" "<<f[n][b].exp<<" "<<f[n][b].cnt<<" "<<f[n][b].exp + f[n][b].cnt * mid<<std::endl;
if(f[n][b].cnt > a)
l = mid;
else
fans = std::max(f[n][b].exp + f[n][b].cnt * mid,fans),r = mid;
}
printf("%.12lf",fans);
}
[八省联考 2018] 林克卡特树
简要题意:在树上选取\(k + 1\)条链的权值总和最大。
该类树上选链的可以使用\(dp\),我们设\(f_{u,j,0/1/2}\)为\(u\)中有\(j\)条完整链,\(0\)表示\(u\),\(0\)在子树背包合并时的点中表示其没被占据,子树背包合并结束时其意义改变为经过\(u\)的那条链在内部消化,或者\(u\)没被用,\(1\)表示其有一条链向父亲连,\(2\)表示子树背包有一条经过\(u\)的完整的内部消化链。
转移显然。
先给一个\(60\)分的直接\(dp\)代码。
其为\(O(n^2k)\)。
[八省联考 2018] 林克卡特树 sub1
#include<bits/stdc++.h>
#define ll long long
#define N 300005
#define K 200
int n,k;
int f[N][K][3];
struct P{
int to,next,v;
}e[N << 1];
int head[N],cnt;
void add(ll x,ll y,ll v){
e[++cnt].to = y;
e[cnt].next = head[x];
e[cnt].v = v;
head[x] = cnt;
}
void dfs(int u,int fa){
f[u][0][0] = f[u][0][1] = f[u][1][2] = 0;
for(int i = head[u];i;i = e[i].next){
int v = e[i].to;
if(v == fa)
continue;
dfs(v,u);
for(int j = k;j;--j){
f[u][j][1] = std::max(f[u][j][1],f[u][j][0] + f[v][0][1] + e[i].v);
for(int l = j - 1;~l;--l){
f[u][j][0] = std::max(f[u][j][0],f[u][l][0] + f[v][j - l][0]);
f[u][j][1] = std::max(f[u][j][1],std::max(f[u][l][1] + f[v][j - l][0],f[u][l][0] + f[v][j - l][1] + e[i].v));
f[u][j][2] = std::max(f[u][j][2],std::max(f[u][l][2] + f[v][j - l][0],f[u][l][1] + f[v][j - l - 1][1] + e[i].v));
}
}
f[u][0][1] = std::max(f[u][0][1],f[v][0][1] + e[i].v);
}
for(int i = 1;i <= k;++i)
f[u][i][0] = std::max(f[u][i][0],std::max(f[u][i - 1][1],f[u][i][2]));
}
int main(){
scanf("%d%d",&n,&k),++k;
for(int i = 1;i < n;++i){
ll x,y,v;
scanf("%lld%lld%lld",&x,&y,&v);
add(x,y,v);
add(y,x,v);
}
memset(f,~0x3f,sizeof(f));dfs(1,0);
std::cout<<f[1][k][0]<<std::endl;
}
然后猜想其对\(k\)有凸性,凸优化一下,但是好像没人证明这个结论,\(O(nlogk)\)。
分治系列
CDQ分治
平面最近点对(加强版)
考虑我们按x分治。
每次按中位数分成两块,然后递归处理。
设两边答案的最小值为\(d\),我们把\(x \in[x - d,x + d]\)的点拉出来按\(y\)排序。
我们枚举每个点,往后暴力枚举,当两点距离\(>d\)时撤销。
证明请见。
平面最近点对(加强版)
#include<bits/stdc++.h>
#define N 2000005
#define ll long long
struct P{
int x,y;
}a[N],b[N];
bool cmp1(P ai,P b){
return ai.x < b.x;
}
bool cmp2(P ai,P b){
return ai.y < b.y;
}
const long long inf=5e18;
long long sqr(int x){return (long long)x*x;}
long long dis(int l,int r){return sqr(a[l].x-a[r].x)+sqr(a[l].y-a[r].y);}
ll dd(P ai,P b){return sqr(ai.x - b.x) + sqr(ai.y - b.y);}
inline ll solve(int l,int r){
if(l >= r)return inf;
if(l + 1 == r)return dis(l,r);
#define mid ((l + r) >> 1)
int cnt = 0;
int t = a[mid].x;
ll d = std::min(solve(l,mid),solve(mid + 1,r));
for(int i = l;i <= r;++i)
if(sqr(a[i].x - t) < d)
b[++cnt] = a[i];
std::sort(b + 1,b + cnt + 1,cmp2);
for(int i = 1;i <= cnt;++i)
for(int j = i + 1;j <= cnt && sqr(b[j].y - b[i].y) < d;++j)
d = std::min(d,dd(b[i],b[j]));
return d;
}
int n;
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;++i)
scanf("%d%d",&a[i].x,&a[i].y);
std::sort(a + 1,a + n + 1,cmp1);
printf("%.4lf",sqrt(solve(1,n)));
}
CF1442D Sum
有结论:一定只会有一个未全部取完的组。
贪心易证。
我们直接分治到最低节点钦定其为未取完的即可,然后处理背包问题。
CF1442D Sum
#include<bits/stdc++.h>
#define ll long long
#define N 3005
int n,k;
ll ans;
ll vi[N];
std::vector<int>a[N];
std::vector<ll>dp(N,0);
inline void sol(int l,int r){
if(l == r){
// std::cout<<l<<std::endl;
// for(int i = 0;i <= k;++i)
// std::cout<<dp[i]<<" ";
// puts("");
ll w = 0,v = 0;
ans = std::max(ans,dp[k]);
for(int i = 0;i < a[l].size();++i)
++w,v += a[l][i],ans = std::max(ans,k - w >= 0 ? dp[k - w] + v : 0ll);
return ;
}
#define mid ((l + r) >> 1)
std::vector<ll> t = dp;
for(int i = l;i <= mid;++i)
for(int j = k;j >= (int)a[i].size();--j)
dp[j] = std::max(dp[j],dp[j - (int)a[i].size()] + vi[i]);
sol(mid + 1,r);
dp = t;
for(int i = mid + 1;i <= r;++i)
for(int j = k;j >= (int)a[i].size();--j)
dp[j] = std::max(dp[j],dp[j - (int)a[i].size()] + vi[i]);
sol(l,mid);
}
int main(){
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;++i){
int l;
scanf("%d",&l);
while(l -- ){
int x;
scanf("%d",&x);
vi[i] += x;
a[i].push_back(x);
}
}
sol(1,n);
std::cout<<ans<<std::endl;
}
【模板】三维偏序(陌上花开)
版。版。板。
【模板】三维偏序(陌上花开)
#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
#define N 100005
#define lowbit(x) (x & -x)
struct P{
ll x,y,z,id;
}e[N];
ll ans[N],unq[N],f[N];
ll t[N * 2];
ll n,k;
void add(ll x,ll p){
for(int i = x;i <= k;i += lowbit(i))
t[i] += p;
}
int get(ll x){
ll ans = 0;
for(int i = x;i;i -= lowbit(i))
ans += t[i];
return ans;
}
bool cmp(P t,P s){
if(t.x != s.x)
return t.x < s.x;
if(t.y != s.y)
return t.y < s.y;
return t.z < s.z;
}
bool cmp1(P t,P s){
if(t.y != s.y)
return t.y < s.y;
if(t.z != s.z)
return t.z < s.z;
return t.x < s.x;
}
void cdq(ll l,ll r){
if(l == r)
return;
int mid = (l + r) >> 1;
cdq(l,mid),cdq(mid + 1,r);
std::sort(e + l,e + r + 1,cmp1);
for(int i = l;i <= r;++i)
if(e[i].x <= mid)
add(e[i].z,1);
else
ans[e[i].id] += get(e[i].z);
for(int i = l;i <= r;++i){
if(e[i].x <= mid)
add(e[i].z,-1);
// printf("%lld %lld\n",e[i].x,ans[e[i].id]);
}
}
int main(){
scanf("%lld%lld",&n,&k);
for(int i = 1;i <= n;++i)
scanf("%lld%lld%lld",&e[i].x,&e[i].y,&e[i].z),e[i].id = i;
std::sort(e + 1,e + n + 1,cmp);
for(int i = 1,j;i <= n;){
j = i + 1;
while(j <= n && e[j].x == e[i].x && e[j].y == e[i].y && e[j].z == e[i].z)
j ++ ;
while(i < j)
unq[e[i].id] = e[j - 1].id,i ++ ;
}
for(int i = 1;i <= n;++i)
e[i].x = i;
cdq(1,n);
for(int i = 1;i <= n;++i)
f[ans[unq[e[i].id]]] ++ ;
for(int i = 0;i < n;++i)
printf("%lld\n",f[i]);
}
[CQOI2011]动态逆序对
考虑把一个点写作\((t,w,v)\)表示其被删除的时间,以及位置,和权值。
则一个点对能贡献一定有\(t_i < t_j\),然后就变成逆序对了。
然后将答案写在\(f_{t_i}\),然后做一个后缀和。
[CQOI2011]动态逆序对
#include<bits/stdc++.h>
#define ll long long
#define N 100005
struct P{
int t,w,v;
}e[N];
int n;
int m;
ll f[N];
int del[N];
inline bool cmp(P a,P b){
return a.t < b.t;
}
inline bool cmp2(P a,P b){
return a.w < b.w;
}
int T[N];
#define lowbit(x) (x & -x)
inline void add(int x,int p){
for(int i = x;i <= n;i += lowbit(i))
T[i] += p;
}
inline int find(int x){
int ans = 0;
for(int i = x;i;i -= lowbit(i))
ans += T[i];
return ans;
}
inline void solve(int l,int r){
#define mid ((l + r) >> 1)
if(l == r)return ;
solve(mid + 1,r);
solve(l,mid);
std::sort(e + l,e + mid + 1,cmp2);
std::sort(e + mid + 1,e + r + 1,cmp2);
// std::cout<<"!"<<l<<" "<<r<<" "<<mid<<std::endl;
// for(int i = mid + 1;i <= r;++i)
// std::cout<<e[i].w<<" ";
// puts("");
int ri = mid + 1;
// std::cout<<"!"<<l<<" "<<r<<" "<<mid<<std::endl;
for(int i = l;i <= mid;++i){//wx < wy vx > vy
// std::cout<<e[i].t<<" "<<e[i].w<<" "<<e[i].v<<std::endl;;
while(e[ri].w < e[i].w && ri <= r)
add(e[ri].v,1),++ri;
// std::cout<<find(n) - find(e[i].v)<<std::endl;
f[e[i].t] += find(n) - find(e[i].v);
}
-- ri;
while(ri >= mid + 1)
add(e[ri].v,-1),--ri;
ri = r;//wx > wy vx < vy
for(int i = mid;i >= l;--i){
// std::cout<<e[i].t<<" "<<e[i].w<<" "<<e[i].v<<std::endl;;
while(e[ri].w > e[i].w && ri >= mid + 1)
add(e[ri].v,1),--ri;
// std::cout<<find(e[i].v - 1)<<std::endl;
f[e[i].t] += find(e[i].v - 1);
}
++ ri;
while(ri <= r)
add(e[ri].v,-1),++ri;
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;++i)
scanf("%d",&e[i].v),e[i].w = i;
for(int i = 1;i <= m;++i){
int x;
scanf("%d",&x);
del[x] = i;
}
for(int i = 1;i <= n;++i){
if(del[e[i].v])
e[i].t = del[e[i].v];
else
e[i].t = m + 1;
}
std::sort(e + 1,e + n + 1,cmp);
solve(1,n);
for(int i = m;i >= 1;--i)
f[i] = f[i + 1] + f[i];
for(int i = 1;i <= m;++i)
std::cout<<f[i]<<std::endl;
}
线段树分治
CF601E A Museum Robbery
把物品打在树上,暴力背包。
CF601E A Museum Robbery
#include<bits/stdc++.h>
#define ll long long
#define N 40007
#define K 1007
#define base ((ll)1e7 + 19)
#define mod ((ll)1e9 + 7)
using std::pair;
using std::vector;
#define pii std::pair<int,int>
#define vii std::vector<pii>::iterator
struct P{
int v,w,l,r;
}e[N];
int k;
std::vector<pii> seg[N << 2];
ll dp[K];
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
#define mid ((l + r) >> 1)
inline void add(int u,int l,int r,int tl,int tr,int v,int w){
if(tl > tr)return ;
if(tl <= l && r <= tr){
seg[u].push_back(std::make_pair(v,w));
return ;
}
if(tl <= mid)
add(ls(u),l,mid,tl,tr,v,w);
if(tr > mid)
add(rs(u),mid + 1,r,tl,tr,v,w);
}
int n,q,opt,u,v,t = 1;
inline void solve(int u,int l,int r,ll *f){
for(vii it = seg[u].begin();it != seg[u].end();++it){
for(int j = k;j >= it -> second;--j)
f[j] = std::max(f[j],f[j - it -> second] + it -> first);
//,std::cout<<it -> first<<" "<<it -> second<<" "<<f[j]<<std::endl
}
// std::cout<<u<<" "<<l<<" "<<r<<std::endl;
// for(int i = 1;i <= k;++i)
// std::cout<<f[i]<<" ";
// puts("");
if(l == r){
ll ans = 0;
for(int i = k;i;--i)
ans = (ans * base + f[i]) % mod;
std::cout<<ans<<std::endl;
return ;
}
ll Q[K];
memcpy(Q,f,sizeof(Q));
solve(ls(u),l,mid,Q);
memcpy(Q,f,sizeof(Q));
solve(rs(u),mid + 1,r,Q);
}
int main(){
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;++i){
scanf("%d%d",&u,&v);
e[i] = (P){u,v,t,-1};
}
scanf("%d",&q);
for(int i = 1;i <= q;++i){
scanf("%d",&opt);
if(opt == 1){
scanf("%d%d",&u,&v);
e[++n] = (P){u,v,t,-1};
}else if(opt == 2){
int x;
scanf("%d",&x);
e[x].r = t - 1;
}else{
++ t;
}
}
--t;
for(int i = 1;i <= n;++i){
e[i].r = e[i].r == -1 ? t : e[i].r;
add(1,1,t,e[i].l,e[i].r,e[i].v,e[i].w);
}
solve(1,1,t,dp);
}
CF813F Bipartite Checking 与 二分图 /【模板】线段树分治
拆点,一个点拆成白点和黑点,一次加边如果两点同色在一个集合则其非法。
要做的就是给修改丢到线段树上,然后搞个可撤销并查集就行了。
线段树下标要对应。
二分图 /【模板】线段树分治
#include<bits/stdc++.h>
#define ll long long
#define N 200005
int n,m,k;
using std::pair;
using std::vector;
#define pii std::pair<int,int>
#define vii std::vector<pii>
vii T[N << 2];
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
#define mid ((l + r) >> 1)
inline void add(int u,int l,int r,int tl,int tr,pii t){
if(tl > tr)return;
if(tl <= l && r <= tr){
T[u].push_back(t);
return ;
}
if(tl <= mid)
add(ls(u),l,mid,tl,tr,t);
if(tr > mid)
add(rs(u),mid + 1,r,tl,tr,t);
}
int fa[N << 1],top;
ll key[N << 1];
bool tag = 0;
int st[(N << 1) * 2];
inline int find(int u){return (u == fa[u]) ? u : find(fa[u]);}
inline void merge(int x,int y){
int fx = find(x),fy = find(y);
if(key[fx] >= key[fy])
std::swap(fx,fy);
st[++top] = fx;
fa[fx] = fy;
}
inline void del(int now){
while(top > now){
fa[st[top]] = st[top];
-- top;
}
}
inline void solve(int u,int l,int r){
int las = top;
tag = 0;
for(int i = 0;i < T[u].size();++i){
pii a = T[u][i];
if(find(a.first) == find(a.second)){
tag = 1;
for(int j = l;j <= r;++j)
puts("No");
break;
}else{
merge(a.first + n,a.second);
merge(a.first,a.second + n);
}
}
if(!tag){
if(l == r)
puts("Yes");
else{
solve(ls(u),l,mid);
solve(rs(u),mid + 1,r);
}
}
del(las);
}
#define fhq_treap time(0)
int main(){
srand(fhq_treap);
scanf("%d%d%d",&n,&m,&k);
for(int i = 1;i <= m;++i){
int x,y,l,r;
scanf("%d%d%d%d",&x,&y,&l,&r);
if(l == r)continue;
add(1,1,k,l + 1,r,std::make_pair(x,y));
}
for(int i = 1;i <= n << 1;++i)
fa[i] = i,key[i] = rand() << 15 | rand();
solve(1,1,k);
}
CF938G Shortest Path Queries
前置知识:[WC2011]最大XOR和路径和[学习笔记] 线性基 ,后者年久失修。
考虑这题实际上是动态问题。
我们维护可撤销线性基以及可撤销并查集表示树结构即可。
和上题代码差不太多,咕咕咕了。
CF576E Painting Edges
考虑这题的难点是我们并不知道一条影响是否会改变下一条
我们不妨假定其染色成功。
我们发现如果染色成功等同于其影响后延,那么我们不撤销操作,否则我们撤销操作。
然后和前面的题一样,不同的是维护\(k\)的并查集即可。
代码咕咕咕。
CF603E Pastoral Oddities
有如下结论:
一定是所有联通块均为偶数点,且加边不影响答案。
考虑一个静态问题:
有一个固定边集我们如何操作。
我们一定是从小到大能加就加。
因为对奇数联通块数量来说加一条边一定不劣。
考虑动态问题。
我们先思考为什么我们不能直接把每条边打在区间上然后操作:
因为不满足最优子结构,我这里选了这条边显然底下会出问题。
但是我们发现:一个最优答案的子结构一定满足最优化(最优化定义为按可选边权依次加入并查集的边。)
我们发现加边不好做,我们不妨思考倒序处理。
那么我们从后往前处理最优化结构:
我们可以确定其中的边集内的边的属于最优结构的范围为\([begin,\max T (i \in best\ when\ in\ T]\)。
那么我们就确定了其中的范围可以在树上打标记了。
很好的题。
CF603E Pastoral Oddities
#include<bits/stdc++.h>
#define N 300005
int n,m,pos,ans[N],odd;
struct P{
int x,y,v,id;
}e[N];
bool operator < (P a,P b){
return a.v < b.v;
}
struct Last{int x,y,dlt;}st[N];//可撤销
int fa[N],siz[N],top;
inline int find(int x){return fa[x] == x ? x : find(fa[x]);}
std::vector<P>vec[N << 2];
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
#define mid ((l + r) >> 1)
inline void cover(int u,int l,int r,int tl,int tr,P v){
if(tl > tr)return;
if(tl <= l && r <= tr){
vec[u].push_back(v);
return ;
}
if(tl <= mid)
cover(ls(u),l,mid,tl,tr,v);
if(tr > mid)
cover(rs(u),mid + 1,r,tl,tr,v);
}
inline void merge(int x,int y){
int fx = find(x),fy = find(y);
if(fx == fy)return;
if(siz[fx] < siz[fy])std::swap(fx,fy);
st[++top] = (Last){fx,fy,0};
if(siz[fx] % 2 && siz[fy] % 2)
odd -= 2,st[top].dlt += 2;
siz[fx] += siz[fy],fa[fy] = fx;
}
inline void solve(int u,int l,int r){
int las = top;
for(int i = 0;i < vec[u].size();++i)
merge(vec[u][i].x,vec[u][i].y);
if(l == r){
while(1){
if(odd == 0 || pos == m)break;
if(e[pos + 1].id <= l){
merge(e[pos + 1].x,e[pos + 1].y);
cover(1,1,m,e[pos + 1].id,l - 1,e[pos + 1]);
}
++ pos;
}
if(odd == 0)ans[l] = e[pos].v;
else ans[l] = -1;
}else{
solve(rs(u),mid + 1,r);
solve(ls(u),l,mid);
}
while(top != las){
int x = st[top].x,y = st[top].y,dlt = st[top].dlt;
siz[x] -= siz[y],fa[y] = y;
odd += dlt;
-- top;
}
}
int main(){
scanf("%d%d",&n,&m);
odd = n;
for(int i = 1;i <= n;++i)
fa[i] = i,siz[i] = 1;
for(int i = 1;i <= m;++i)
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].v),e[i].id = i;
std::sort(e + 1,e + m + 1);
solve(1,1,m);
for(int i = 1;i <= m;++i)
std::cout<<ans[i]<<std::endl;
}
二维分治
CF364E Empty Rectangles
考虑横竖交替分治。
维护\(k\)个指针表示:在分治线上和线下的和为\(x\)的边界。
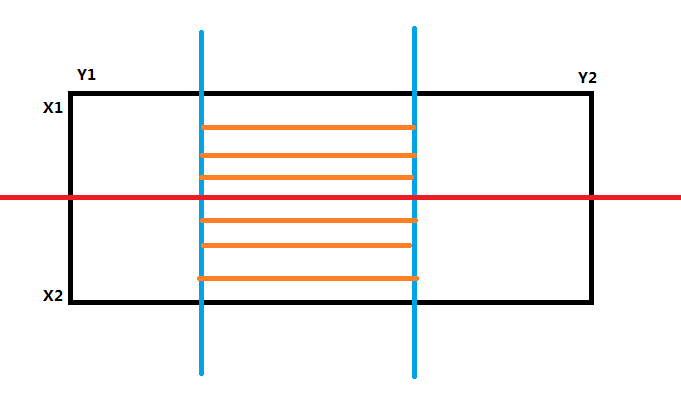
我们枚举矩形的左边界 \(i\),然后把右边界当成指针一直往右扫,过程中维护"橙线",也就是达到 \(x\) 个 \(1\) 的边界。显然随着右边界的移动上面橙线只会下移,下面的橙线只会上移,这个是具有单调性的,可以维护 \(k\) 个指针,算答案的时候还是简单乘法原理。
CF364E Empty Rectangles
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 2505;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,a[M][M],b[M][M],up[2][10];ll ans;
int cal(int xl,int xr,int yl,int yr)
{
return b[xr][yr]-b[xr][yl]-b[xl][yr]+b[xl][yl];
}
void cdq(int xl,int xr,int yl,int yr,int ty)
{
if(xl==xr || yl==yr) return ;
if(xl+1==xr && yl+1==yr)
{
ans+=(cal(xl,xr,yl,yr)==k);
return ;
}
if(ty==0)
{
int mid=(xl+xr)>>1;
cdq(xl,mid,yl,yr,1);
cdq(mid,xr,yl,yr,1);
for(int i=yl;i<=yr;i++)
{
up[0][0]=up[1][0]=mid;
for(int j=1;j<=k+1;j++)
up[0][j]=xl,up[1][j]=xr;
for(int j=i+1;j<=yr;j++)
{
for(int p=1;p<=k+1;p++)
{
while(cal(up[0][p],mid,i,j)>=p)
up[0][p]++;
while(cal(mid,up[1][p],i,j)>=p)
up[1][p]--;
}
for(int p=0;p<=k;p++)
ans+=(up[0][p]-up[0][p+1])
*(up[1][k-p+1]-up[1][k-p]);
}
}
}
else
{
int mid=(yl+yr)>>1;
cdq(xl,xr,yl,mid,0);
cdq(xl,xr,mid,yr,0);
for(int i=xl;i<=xr;i++)
{
up[0][0]=up[1][0]=mid;
for(int j=1;j<=k+1;j++)
up[0][j]=yl,up[1][j]=yr;
for(int j=i+1;j<=xr;j++)
{
for(int p=1;p<=k+1;p++)
{
while(cal(i,j,up[0][p],mid)>=p)
up[0][p]++;
while(cal(i,j,mid,up[1][p])>=p)
up[1][p]--;
}
for(int p=0;p<=k;p++)
ans+=(up[0][p]-up[0][p+1])
*(up[1][k-p+1]-up[1][k-p]);
}
}
}
}
signed main()
{
n=read();m=read();k=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
scanf("%1d",&a[i][j]);b[i][j]+=a[i][j];
}
cdq(0,n,0,m,1);
printf("%lld\n",ans);
}
整体二分
[POI2011]MET-Meteors
考虑其二分是非常简单的。
贡献的时候拆环就行了。
然后可以相当于是个整体二分板子。
同时其也利用了分治中心移动距离\(O(nlog)\)的操作保证了复杂度。
[POI2011]MET-Meteors
#include<bits/stdc++.h>
#define ll unsigned long long
#define N 300010
#define int ll
int n,m,belong[N],ls[N],rs[N],target[N],k;
int val[N],now,cont[N],lt[N],rt[N],ans[N];
ll tree[N],tc[N];
using std::vector;
std::vector<int>T[N];
#define lowbit(x) (x & -x)
inline void add(int x,int p){
for(int i = x;i <= m;i += lowbit(i))
tree[i] += p;
}
inline ll find(int x){
ll ans = 0;
for(int i = x;i;i -= lowbit(i))
ans += tree[i];
return ans;
}
inline void change(int l,int r,int x){
if(l <= r){
add(l,x);
add(r + 1,-x);
}else{
add(l,x),add(m + 1,-x);
add(1,x),add(r + 1,-x);
}
}
int t;
#define mid ((l + r) >> 1)
inline void query(int l,int r,int L,int R){
if(l > r)return;if(L > R)return ;
// std::cout<<l<<" "<<r<<std::endl;
// for(int i = L;i <= R;++i)
// std::cout<<cont[i]<<" ";
// puts("");
if(l == r){
for(int i = L;i <= R;++i)
ans[cont[i]] = l;
return ;
}
while(now < mid)++now,change(ls[now],rs[now],val[now]);
while(now > mid)change(ls[now],rs[now],-val[now]),--now;
for(int i = L;i <= R;++i){
tc[cont[i]] = 0;
for(int j =0;j < T[cont[i]].size();++j)
tc[cont[i]] += find(T[cont[i]][j]);
}
int lct = 0,rct = 0;
for(int i = L;i <= R;++i){
if(tc[cont[i]] >= target[cont[i]])
lt[++lct] = cont[i];
else
rt[++rct] = cont[i];
}
int split = lct;
// puts("LC");
// for(int i = 1;i <= lct;++i)
// std::cout<<lt[i]<<" ";
// puts("");
// puts("RC");
// for(int i = 1;i <= rct;++i)
// std::cout<<rt[i]<<" ";
// puts("");
for(int i = 1;i <= lct;++i)
cont[i + L - 1] = lt[i];
for(int i = 1;i <= rct;++i)
cont[L + lct + i - 1] = rt[i];
query(l,mid,L,L + split - 1);
query(mid + 1,r,L + split,R);
}
signed main(){
scanf("%llu%llu",&n,&m);
for(int i = 1;i <= m;++i){
scanf("%llu",&belong[i]);
T[belong[i]].push_back(i);
}
for(int i = 1;i <= n;++i){
scanf("%llu",&target[i]);
cont[i] = i;
}
scanf("%llu",&k);
for(int i = 1;i <= k;++i){
scanf("%llu%llu%llu",&ls[i],&rs[i],&val[i]);
}
++ k;
ls[k] = 1;
rs[k] = m;
val[k] = 0x3f3f3f3f;
now = 0;
query(1,k,1,n);
for(int i = 1;i <= n;++i){
if(ans[i] == k)
puts("NIE");
else
std::cout<<ans[i]<<std::endl;
}
return 0;
}
[国家集训队]矩阵乘法
整体二分板板。
[国家集训队]矩阵乘法
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 3e5 + 50, INF = 0x3f3f3f3f;
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
int n, q, len, c[maxn], a[505][505], tree[505][505], ans[maxn], mp[maxn];
vector <int> res;
vector <pair <int, int> > pos[maxn];
struct Node {
int x1, y1, x2, y2, k;
} b[maxn];
inline void Insert (register int x, register int y) {
for (register int i = x; i <= n; i += i & -i)
for (register int j = y; j <= n; j += j & -j)
tree[i][j] ++;
}
inline void Delete (register int x, register int y) {
for (register int i = x; i <= n; i += i & -i)
for (register int j = y; j <= n; j += j & -j)
tree[i][j] --;
}
inline int Query (register int x, register int y, register int ans = 0) {
for (register int i = x; i; i -= i & -i)
for (register int j = y; j; j -= j & -j)
ans += tree[i][j];
return ans;
}
inline void Binary (register int l, register int r, vector <int> vec) {
if (! vec.size ()) return;
if (l == r) {
for (register int i = 0; i < vec.size (); i ++) ans[vec[i]] = mp[l];
return;
}
register int mid = (l + r) >> 1;
vector <int> vec0, vec1;
for (register int x = l; x <= mid; x ++)
for (register int i = 0; i < pos[x].size (); i ++)
Insert (pos[x][i].first, pos[x][i].second);
for (register int i = 0; i < vec.size (); i ++) {
register int id = vec[i], x1 = b[id].x1, y1 = b[id].y1, x2 = b[id].x2, y2 = b[id].y2;
register int sum = Query (x2, y2) - Query (x1 - 1, y2) - Query (x2, y1 - 1) + Query (x1 - 1, y1 - 1);
if (sum >= b[id].k) vec0.push_back (id);
else b[id].k -= sum, vec1.push_back (id);
}
for (register int x = l; x <= mid; x ++)
for (register int i = 0; i < pos[x].size (); i ++)
Delete (pos[x][i].first, pos[x][i].second);
Binary (l, mid, vec0), Binary (mid + 1, r, vec1);
}
int main () {
n = read(), q = read();
for (register int i = 1; i <= n; i ++)
for (register int j = 1; j <= n; j ++)
a[i][j] = c[++ len] = read();
sort (c + 1, c + len + 1), len = unique (c + 1, c + len + 1) - c - 1;
for (register int i = 1; i <= n; i ++) {
for (register int j = 1; j <= n; j ++) {
register int res = lower_bound (c + 1, c + len + 1, a[i][j]) - c;
mp[res] = a[i][j], a[i][j] = res, pos[res].push_back (make_pair (i, j));
}
}
for (register int i = 1; i <= q; i ++)
b[i].x1 = read(), b[i].y1 = read(), b[i].x2 = read(), b[i].y2 = read(), b[i].k = read(), res.push_back (i);
Binary (1, len, res);
for (register int i = 1; i <= q; i ++) printf ("%d\n", ans[i]);
return 0;
}
决策单调性分治
CF868F Yet Another Minimization Problem
待会写个四边形不等式的博。
这是一个 2D/1D 动态规划问题。
每次对一维通过上一维dp过来。
这是一个 1D/1D 动态规划问题。
前文我们提到,1D/1D问题可以考虑CDQ分治,但我们需要在合并两段区间时也能做到对右子区间做到\(O(n)\)。
但是这题的贡献并不满足这个条件。
我们转而思考,这类区间贡献的方式是否拥有决策单调性。
下面证明该问题具有决策单调性:
即证明\(\forall i_1 < i_2\),假设其转移点为\(x_1,x_2\),那么有\(x_1\leq x_2\)。
假设若有\(x_1 > x_2\),则有\(f_{x_1} + w_{x_1 + 1,i1} \leq f_{x_2} + w_{x_2 + 1,i2}\),\(f_{x_1} + w_{x_2 + 1,i1} \leq f_{x_2} + w_{x_1 + 1,i2}\)
若两等号均成立知其不影响证明。
若有一个取了小于:不妨假设其为\(f_{x_1} + w_{x1 + 1,i1} \leq f_{x_2} + w_{x2 + 1,i2}\).\(f_{x_1} + w_{x_2 + 1,i1} < f_{x_2} + w_{x_1 + 1,i2}\)
整理可得\(w_{x_1 + 1,i1} - w_{x_2 + 1,i1} < w_{x_1 + 1,i2} - w_{x_2 + 1,i2}\)
由\(i1 < i2\)知其错误。
则结论得证。
可分治解决该问题。
具体可以看代码。
其中利用了两个指针在分治过程移动距离不过\(O(nlogn)\)
CF868F Yet Another Minimization Problem
#include<bits/stdc++.h>
#define ll long long
#define N 100005
int n,k;
int buc[N],L,R,a[N];
ll ans;
inline void up(int c,int d){ans += d * buc[c] * 1ll * (buc[c] - 1) / 2;}
inline ll cal(int l,int r){
while(L < l)up(a[L],-1),buc[a[L]] -- ,up(a[L],1),++L;
while(L > l)L -- ,up(a[L],-1),buc[a[L]] ++ ,up(a[L],1);
while(R > r)up(a[R],-1),buc[a[R]] -- ,up(a[R],1),R --;
while(R < r)R ++ ,up(a[R],-1),buc[a[R]] ++ ,up(a[R],1);
return ans;
}
ll dp[22][N];
int cur;
inline void solve(int lb,int rb,int l,int r){
if(lb > rb || l > r)return ;
int d = 0;
ll res = 1e18;
#define mid ((l + r) >> 1)
for(int i = lb;i <= rb;++i){
ll tmp = cal(i + 1,mid);
if(res > dp[cur - 1][i] + tmp) res = dp[cur - 1][i] + tmp,d = i;
}
dp[cur][mid] = res;
solve(lb,d,l,mid - 1),solve(d,rb,mid + 1,r);
}
int main(){
std::memset(dp,0x3f,sizeof(dp));
dp[0][0] = 0;
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;++i)
scanf("%d",&a[i]);
buc[a[1]] ++ ,L = R = 1;
for(cur = 1;cur <= k;++cur)
solve(0,n - 1,1,n);
std::cout<<dp[k][n]<<std::endl;
}
树分治
点分治
CF150E Freezing with Style
二分答案。
树上启发式合并单调队列。
淀粉质上去就行了。
CF150E Freezing with Style
#include <cstdio>
#include <vector>
#include <algorithm>
const int Inf = 0x3f3f3f3f;
const int MN = 100005;
int N, L, R, Ans = -1, AnsU, AnsV;
int uv[MN], w[MN];
std::vector<int> G[MN];
int dw[MN], M;
int vis[MN], siz[MN], tsiz, rsiz, Root;
void GetRoot(int u, int fz) {
siz[u] = 1;
int nsiz = 0;
for (auto i : G[u]) {
int v = uv[i] ^ u;
if (v == fz || vis[v]) continue;
GetRoot(v, u), siz[u] += siz[v];
if (nsiz < siz[v]) nsiz = siz[v];
}
if (nsiz < tsiz - siz[u]) nsiz = tsiz - siz[u];
if (rsiz > nsiz) rsiz = nsiz, Root = u;
}
int stk[MN], tp, _U;
inline bool cmp(int i, int j) {
return siz[uv[i] ^ _U] < siz[uv[j] ^ _U];
}
int seq[MN], sequ[MN], odep, tmp[MN], tmpu[MN], ndep;
void DFS(int u, int fz, int d, int x, int y) {
if (tmp[d] < x) tmp[d] = x, tmpu[d] = u;
if (ndep < d) ndep = d;
for (auto i : G[u]) {
int v = uv[i] ^ u;
if (v == fz || vis[v]) continue;
DFS(v, u, d + 1, x + (w[i] >= y ? 1 : -1), y);
}
}
int ucal, vcal;
bool Calc(int u, int x) {
static int que[MN];
seq[odep = 0] = 0, sequ[0] = u;
for (int i = 1; i <= tp; ++i) {
int v = uv[stk[i]] ^ u;
for (int j = 1; j <= siz[v]; ++j) tmp[j] = -Inf;
ndep = 0, DFS(v, u, 1, w[stk[i]] >= x ? 1 : -1, x);
int l = 1, r = 0, lb = odep, rb = odep + 1;
for (int j = 1; j <= ndep; ++j) {
while (rb > 0 && rb > L - j) {
--rb;
while (l <= r && seq[que[r]] < seq[rb]) --r;
que[++r] = rb;
}
while (lb >= 0 && lb > R - j) {
--lb;
while (l <= r && que[l] > lb) ++l;
}
if (l <= r && seq[que[l]] + tmp[j] >= 0) {
ucal = sequ[que[l]], vcal = tmpu[j];
return 1;
}
}
while (odep < ndep) seq[++odep] = -Inf;
for (int j = 1; j <= ndep; ++j)
if (seq[j] < tmp[j])
seq[j] = tmp[j], sequ[j] = tmpu[j];
}
return 0;
}
void Solve(int u) {
int nsiz = tsiz;
tp = 0;
for (auto i : G[u]) {
int v = uv[i] ^ u;
if (vis[v]) continue;
siz[v] = siz[v] > siz[u] ? nsiz - siz[u] : siz[v];
stk[++tp] = i;
}
_U = u, std::sort(stk + 1, stk + tp + 1, cmp);
int lb = 1, rb = M, mid, ans = 0, ansu = 0, ansv = 0;
while (lb <= rb) {
mid = (lb + rb) >> 1;
if (Calc(u, dw[mid])) {
ans = mid;
ansu = ucal, ansv = vcal;
lb = mid + 1;
}
else rb = mid - 1;
}
if (Ans < dw[ans]) {
Ans = dw[ans];
AnsU = ansu, AnsV = ansv;
}
vis[u] = 1;
for (auto i : G[u]) {
int v = uv[i] ^ u;
if (vis[v]) continue;
rsiz = tsiz = siz[v], GetRoot(v, 0), Solve(Root);
}
}
int main() {
scanf("%d%d%d", &N, &L, &R);
for (int i = 1; i < N; ++i) {
int x, y;
scanf("%d%d%d", &x, &y, &w[i]);
uv[i] = x ^ y;
G[x].push_back(i);
G[y].push_back(i);
dw[i] = w[i];
}
std::sort(dw + 1, dw + N);
M = std::unique(dw + 1, dw + N) - dw - 1;
rsiz = tsiz = N, GetRoot(1, 0), Solve(Root);
printf("%d %d\n", AnsU, AnsV);
return 0;
}
淀粉树
写吐了兄弟。
【模板】点分树 | 震波
建出点分树。
然后用两个BIT来询问的时候容斥。
【模板】点分树 | 震波
#include <vector>
#include <cstdio>
#include <iostream>
#include <algorithm>
const int N = 4e5 + 5;
int n, m, val[N];
struct Edge { int to, next; } e[N << 1];
int head[N], cnt = 0;
void Add(int x, int y) {
e[++cnt].next = head[x];
e[cnt].to = y;
head[x] = cnt;
}
int dep[N], siz[N], fa[N];
int pos[N], lg[N << 1], st[N << 1][21], scnt = 0;
void Dfs1(int u, int f) {
st[++cnt][0] = u;
pos[u] = cnt;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (v == f)
continue;
dep[v] = dep[u] + 1;
Dfs1(v, u);
st[++cnt][0] = u;
}
}
int GetMin(int x, int y) {
return dep[x] < dep[y] ? x : y;
}
void GetST()
{
lg[1] = 0;
for(int i = 2; i <= cnt; ++i)
lg[i] = lg[i >> 1] + 1;
for(int j = 1; 1 << j <= cnt; j++)
for(int i = 1; i + (1 << j) <= cnt; i++)
st[i][j] = GetMin(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
int GetDis(int u, int v) {
if (pos[u] > pos[v])
std :: swap(u, v);
int pu = pos[u], pv = pos[v];
int len = pv - pu +1;
return dep[u] + dep[v] - 2 * dep[GetMin(st[pu][lg[len]], st[pv - (1 << lg[len]) + 1][lg[len]])];
}
std :: vector <int> tr[2][N];
void Modify(int u, int opt, int x, int v) {
// printf("siz%d\n", siz[u]);
x++;
for (int i = x; i <= siz[u]; i += i & -i)
tr[opt][u][i] += v;
}
int Query(int u, int opt, int x) {
int res = 0;
x = std :: min(x + 1, siz[u]);
for (int i = x; i; i -= i & -i)
res += tr[opt][u][i];
return res;
}
int tot, rt, vis[N << 1], mn;
void FindRt(int u, int f) {
siz[u] = 1;
int res = 0;
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (v == f || vis[v])
continue;
FindRt(v, u);
siz[u] += siz[v];
res = std :: max(res, siz[v]);
}
res = std :: max(res, tot - siz[u]);
if (res < mn)
mn = res, rt = u;
}
void Dfs2(int u) {
vis[u] = 1;
siz[u] = tot + 1;
tr[0][u].resize(siz[u] + 1);
tr[1][u].resize(siz[u] + 1);
for (int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if (vis[v])
continue;
tot = siz[v];
rt = 0;
mn = 1e9;
FindRt(v, 0);
fa[rt] = u;
Dfs2(rt);
}
}
void Calc(int u ,int w) {
for (int i = u; i; i = fa[i])
// printf("dis%d\n", GetDis(u, i)),
Modify(i, 0, GetDis(u, i), w);
for (int i = u; fa[i]; i = fa[i])
// printf("dis%d\n", GetDis(u, fa[i])),
Modify(i, 1, GetDis(u, fa[i]), w);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &val[i]);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d%d", &u, &v);
Add(u, v);
Add(v, u);
}
Dfs1(1, 0);
GetST();
tot = n;
mn = 1e9;
FindRt(1, 0);
Dfs2(rt);
for (int i = 1; i <= n; i++)
Calc(i, val[i]);
int lst = 0;
// for (int i = 1; i <= n; i++)
// printf("%d ", GetDis(i, i + 2));
// puts("");
while (m--) {
int opt, x, y;
scanf("%d%d%d", &opt, &x, &y);
x ^= lst, y ^= lst;
if (opt == 0) {
lst = 0;
lst += Query(x, 0, y);
for (int i = x; fa[i]; i = fa[i])
if (y >= GetDis(x, fa[i]))
lst += Query(fa[i], 0, y - GetDis(x, fa[i])) - Query(i, 1, y - GetDis(x, fa[i]));
printf("%d\n", lst);
}
else {
Calc(x, y - val[x]);
val[x] = y;
}
}
}
[HNOI2015]开店
和上面那个题差不多。
真写不动了。/tuu。
为了提升分治操作,准备找一天挑战紫荆花之恋。
终于了结束了啊,分治专题。
启发式合并
长链启发式合并
CF1009F Dominant Indices
板板题。
没有采用指针方式,而是使用了\(vector\)
CF1009F Dominant Indices
#include<bits/stdc++.h>
#define ll long long
#define N 1000005
std::vector<int>e[N],f[N];
int fa[N],len[N],son[N];
int ans[N];
int n;
inline void dfs1(int u,int f){//find_len_rt
// std::cout<<u<<" "<<f<<std::endl;
fa[u] = f;
for(auto v : e[u]){
if(v == f)continue;
dfs1(v,u);
if(len[v] >= len[son[u]])
son[u] = v,len[u] = len[v] + 1;
}
}
inline void dfs2(int u){
if(son[u]){
dfs2(son[u]);
std::swap(f[u],f[son[u]]);
f[u].push_back(1);
ans[u] = ans[son[u]];
if(f[u][ans[u]] == 1)ans[u] = len[u];
for(auto v : e[u]){
// std::cout<<v<<std::endl;
if(v == fa[u] || v == son[u])continue;
dfs2(v);
for(int i = len[v];i >= 0;--i){
int tmp = i + len[u] - len[v] - 1;
f[u][tmp] += f[v][i];
if(f[u][tmp] > f[u][ans[u]])
ans[u] = tmp;
else
if(f[u][tmp] == f[u][ans[u]] && tmp > ans[u])
ans[u] = tmp;
}
}
}else{
f[u].push_back(1);
ans[u] = 0;
}
// std::cout<<u<<std::endl;
// for(int i = len[u];i >= 0;--i)
// std::cout<<f[u][i]<<" ";
// puts("");
}
int main(){
scanf("%d",&n);
for(int i = 1;i < n;++i){
int x,y;
scanf("%d%d",&x,&y);
e[x].push_back(y);
e[y].push_back(x);
}
dfs1(1,0);
dfs2(1);
for(int i = 1;i <= n;++i)
printf("%d\n",len[i] - ans[i]);
}
CF1499F Diameter Cuts
考虑\(dp\)。
令\(f_{u,i}\)为\(u\)子树里能到达\(u\)的最大深度为\(i\),且子树合法的方案数。
有断边和不断边两种转移
\(f_{u,max(i,j + 1)} = f_{u,i} * f_{v,j} (i + j + 1 < k)\)
\(f_{u,i} = f_{u,i} * f_{v,j} (j < k)\)
套用转移即可。
这题甚至\(O(n^2)\)可过。
倍增
[SCOI2015]国旗计划
如果他不是环。
那简直是典中典题。
考虑记录\(f_{i,j}\)即从\(i\)处使用了\(2^j\)个区间达到的最右边的处。
环就直接扩展\(2\)倍。
[SCOI2015]国旗计划
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
using namespace std;
int n, m, res[200005];
struct soldier {
int id, l, r;
} s[400005];
int cmp(soldier a, soldier b)
{
return a.l < b.l;
}
int go[400005][20];
void pre()
{
for(int i = 1, p = i; i <= 2 * n; i++) {
while(p <= 2 * n && s[p].l <= s[i].r)
p++;
int pos = p - 1;
go[i][0] = pos;
}
for(int i = 1; i < 20; i++) {
for(int j = 1; j <= 2 * n; j++) {
go[j][i] = go[go[j][i - 1]][i - 1];
}
}
}
void search(int k)
{
int lmt = s[k].l + m, ans = 1, p = k;
for(int i = 19; i >= 0; i--) {
if(go[k][i] != 0 && s[go[k][i]].r < lmt) {
ans += (1 << i);
k = go[k][i];
}
}
res[s[p].id] = ans + 1;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> s[i].l >> s[i].r;
if(s[i].r < s[i].l)
s[i].r += m;
s[i].id = i;
}
sort(s + 1, s + 1 + n, cmp);
for(int i = 1; i <= n; i++) {
s[i + n] = s[i];
s[i + n].l = s[i].l + m;
s[i + n].r = s[i].r + m;
}
pre();
for(int i = 1; i <= n; i++)
search(i);
for(int i = 1; i <= n; i++)
cout << res[i] << " ";
return 0;
}
扫描线
略。(题单上来的时候扫描线已经全做完了)
分块
数论分块
略。该技巧在某些反演题中反复出现。
操作分块
[APIO2019]桥梁
考虑如果没有修改操作,我们显然排序并查集可做。
但是有了修改操作。
我们发现无法快速维护,这个时候我们用到操作分块。
我们把操作分为\(S\)块,我们依次处理块内问题。
我们依次处理每个块,把每个块前的修改都修改。
然后将询问与修改按权排序,枚举询问,先把在块内未被修改过的操作给他永久加入。
然后我们对询问将满足他条件的加入,处理完这个询问之后就暴力撤销。
其一个块的复杂度为\(O(mlogm + S^2logn)\)
调一调块长,取块长为\(750 ~ 780\)好像能跑的飞快。
贡献卡常记录。
[APIO2019]桥梁
#include<bits/stdc++.h>
#define ll long long
#define N 100005
int n,m;
inline int read(){
int ans = 0,f = 1;
char a = getchar();
while(a != '-' && !(a <= '9' && a >= '0'))
a = getchar();
while(a <= '9' && a >= '0')
ans = (ans << 1) + (ans << 3) + (a - '0'),a = getchar();
return f * ans;
}
struct P{
int x,y,p;// x <-> y color : p
int id;
}e[N],D[N];//have_done_edge
inline bool cmp1(P a,P b){
return a.p > b.p;
}
inline bool cmp2(P a,P b){
return a.id < b.id;
}
struct All{
int x,y,tim;//b_x -> y or form x up with color y
}C[N],Q[N];
inline bool cmp(All a,All b){
return a.y > b.y;
}
inline bool cmp3(All a,All b){
return a.tim > b.tim;
}
inline bool cmp5(All a,All b){
return a.tim < b.tim;
}
int fa[N],sz[N];
int stk[N],top;//can _ del _ DSU
int stk2[N];
int q;
int now = 1;
int B = 750;
int ccnt,qcnt;
int fans[N];
int rk[N];
int siz[N];
bool vis[N],used[N];
inline void cancel(int las){
while(top != las){
// std::cout<<"del"<<stk[top]<<" "<<stk2[top]<<std::endl;
fa[stk[top]] = stk[top];
siz[stk2[top]] -= siz[stk[top]];
-- top;
}
}
inline int find(int x){return fa[x] == x ? x : find(fa[x]);}
inline void merge(int x,int y){
int fx = find(x),fy = find(y);
// std::cout<<x<<" "<<y<<std::endl;
if(fx == fy)return;
if(rk[fx] > rk[fy])std::swap(fx,fy);
fa[fx] = fy;
siz[fy] += siz[fx];
stk[++top] = fx;
stk2[top] = fy;
}
inline void del(){
int R = std::min(now + B,q);
int L = now;
ccnt = qcnt = 0;
for(int i = 1;i <= m;++i)
e[i] = D[i];
for(int i = 1;i <= n;++i)
fa[i] = i,siz[i] = 1;
top = 0;
for(;now <= R;++now){
int opt = read(),x = read(),y = read();
// scanf("%d%d%d",&opt,&x,&y);
// std::cout<<now<<std::endl;
// std::cout<<opt<<" "<<x<<" "<<y<<std::endl;
if(opt == 1){
C[++ccnt].x = x;
C[ccnt].y = y;
C[ccnt].tim = now;
}else{
Q[++qcnt].x = x;
Q[qcnt].y = y;
Q[qcnt].tim = now;
}
}
for(int i = 1;i <= m;++i)
vis[i] = 0;
for(int i = 1;i <= ccnt;++i)
vis[C[i].x] = 1;
for(int i = 1;i <= m;++i)
if(vis[i])
C[++ccnt].x = i,C[ccnt].y = e[i].p,C[ccnt].tim = 0;
std::sort(e + 1,e + m + 1,cmp1);
std::sort(Q + 1,Q + qcnt + 1,cmp);
std::sort(C + 1,C + ccnt + 1,cmp3);
// puts("Stand edge");
// for(int i = 1;i <= m;++i)
// std::cout<<e[i].x<<" "<<e[i].y<<" "<<e[i].p<<" "<<vis[i]<<std::endl;
int done = 1;
for(int i = 1;i <= qcnt;++i){
// puts("Query");
// std::cout<<Q[i].x<<" "<<Q[i].y<<" "<<Q[i].tim<<std::endl;
// std::cout<<"match"<<" "<<e[done].p<<std::endl;
while(e[done].p >= Q[i].y && done <= m){
if(!vis[e[done].id]){
merge(e[done].x,e[done].y);
}
++ done;
}
// puts("Change");
int las = top;
for(int j = 1;j <= ccnt;++j){
// std::cout<<C[j].x<<" "<<C[j].y<<" "<<C[j].tim<<" "<<used[C[j].x]<<std::endl;
if(C[j].tim <= Q[i].tim && !used[C[j].x]){
used[C[j].x] = 1;
if(C[j].y >= Q[i].y)
merge(D[C[j].x].x,D[C[j].x].y);
}
}
for(int j = 1;j <= ccnt;++j)
used[C[j].x] = 0;
fans[Q[i].tim] = siz[find(Q[i].x)];
// std::cout<<"getans"<<find(Q[i].x)<<" "<<siz[find(Q[i].x)]<<std::endl;
cancel(las);//回退到las
// puts("cancel_done");
// for(int j = 1;j <= n;++j)
// std::cout<<fa[j]<<" "<<siz[j]<<std::endl;
}
// std::sort(e + 1,e + m + 1,cmp2);
// std::sort(C + 1,C + ccnt + 1,cmp5);
for(int i = ccnt;i >= 1;--i){
// std::cout<<C[i].x<<" "<<C[i].y<<std::endl;
D[C[i].x].p = C[i].y;
}
}
template <typename T>
void write(T x)
{
if(x < 0) {
putchar('-');
x = -x;
}
if(x > 9)
write(x/10);
putchar(x % 10 + '0');
return;
}
int main(){
std::srand(time(0));
n = read(),m = read();
for(int i = 1;i <= n;++i)
rk[i] = rand() << 15 | rand(),siz[i] = 1;
for(int i = 1;i <= m;++i){
int x,y,c;
x = read();
y = read();
c = read();
e[i].x = x,e[i].y = y,e[i].p = c,e[i].id = i;
D[i] = e[i];
}
q = read();
while(now <= q){
del();//del with the block
}
for(int i = 1;i <= q;++i)
if(fans[i])
write(fans[i]),puts("");
}
/*
7 8
1 2 5
1 6 5
2 3 5
2 7 5
3 4 5
4 5 5
5 6 5
6 7 5
5
1 1 1
1 2 3
1 5 2
1 3 1
2 4 2
*/
CF1588F Jumping Through the Array
考虑操作分块。
考虑每个块只会有\(B\)个操作。
那么我们把操作的点作为黑点。
我们发现其黑点的个数只有\(O(B)\)个。
那么我们把一串白色的点给他全合并,则其是静态的。
其这样的白色链也为\(O(B)\)。
操作二,我们直接\(O(B)\)暴力更改其所在环的白链的\(\Delta\)。
操作三,我们直接\(O(1)\)交换两黑点所在的置换环的答案。
查询时我们直接查询每个白链其在二分\([l,r]\)的答案以及暴力枚举黑点。
其复杂度为\(O(\frac{q}{B} * n + q * (B + B log n) )\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号