浅谈卡特兰数
前言:
本身
我们先来看一下这个数列本身:
数列的前几项为:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862。
请记住这些特殊的数字,在信息学竞赛里许多题目都有这个数列的存在,可以在找规律时激发灵感。
意义:
卡特兰数作为广泛出现在OI中的一类特殊数列,其拥有广泛的意义。
这里我们仅选择一个经典例子作为讲解
折线问题:
在平面上,从 \((0,0)\) 走至 \((n,n)\) ,每次只能向上或者向右走,不穿过 \(y = x\) 这条直线有多少种方案。
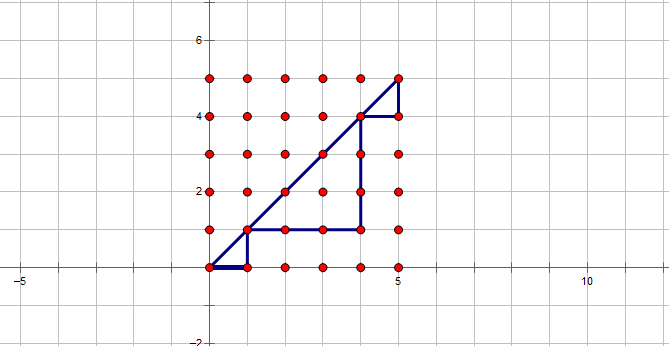
这里给出了一个可行方案。
\(Ans\):
我们考虑我们枚举最后一个在 \(y = x\) 上的一个点 \((i,i)\) 可以考虑把问题规模缩小。
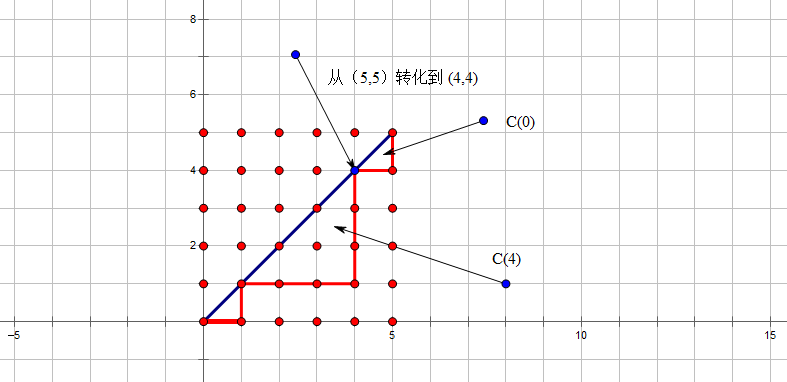
因为我们强制最后一段不能碰到 \(y = x\),所以我们发现在 \((i,i)\) 继续向终点走的过程中,第一步只能向右走,到\((n,n)\)的最后一步只能向上走,中间的问题我们可以视作从 \((i,i + 1)\) 走到 \((n,n - 1)\) 不穿过 \(y = x - 1\)这条直线的方案数,我们平移一下:
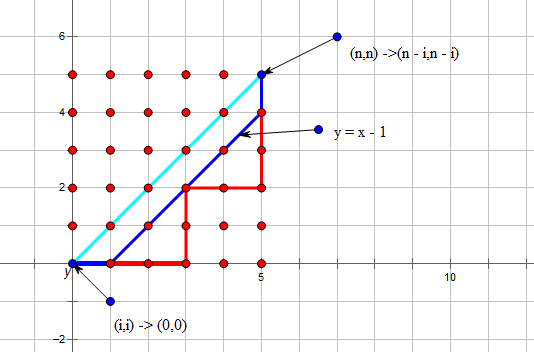
我们发现中间这段的答案其实就是\(C_{n - i - 1}\)。
即可以求出\(C_n = \sum\limits_{i = 0}^{n - 1} C_iC_{n - i - 1}\)。
在众多卡特兰数所对应的题目如出栈顺序,括号匹配中,缩小问题规模是一个很经典的做法。
但我们发现这样直接计算,是一个 \(O(n^2)\) 的过程,其复杂度不尽如意。
我们思考是否能够得到一个 \(O(n)\) 或者 \(O(1)\) 的递推或者通项。
通项
考虑我们进行一个容斥的过程:
我们用所有路径数减去不合法路径的数量。
我们发现所有路径即 \(\binom{2n}{n}\) 。
我们转而思考不合法路径的数量。
我们考虑把一条不合法路径进行操作:
把一条不合法路径在第一次触碰到 \(y = x + 1\) 这条线的点设作 \(p\) ,我们把在 \(p\) 右侧的在 \(y = x + 1\) 以下的部分全部沿 \(y = x + 1\)对称到上方,我们发现这样翻转之后,所有可能出现的不合法路径,和\((0,0) \to (n - 1,n + 1)\) 的路径产生了一一映射的关系。
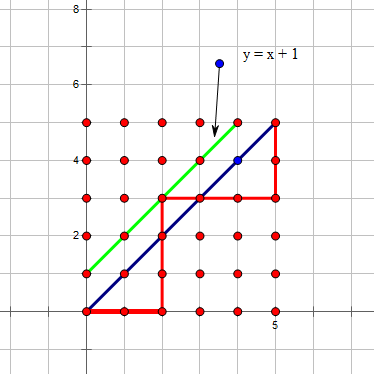
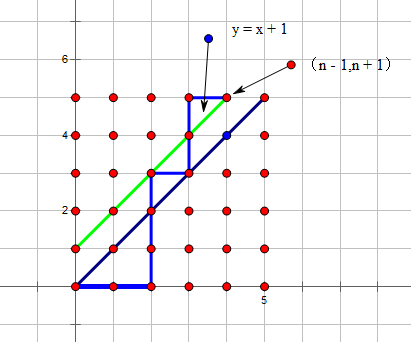
所以我们就有 \(C_n = \binom{2n}{n} - \binom{2n}{n - 1} = \frac{1}{n + 1}\binom{2n}{n}\)。
生成函数:
就和斐波那契数列一样,我们一样可以用处理数列的有力工具生成函数来处理卡特兰数:
我们设 \(C_n\) 的生成函数为 \(H(x)\)。
我们发现卡特兰数的递推式和卷积形式相似,所以我们用卷积来构造 \(H(x)\)。
\(\begin{align*} H(x) &= \sum\limits_{n\geq 0}\sum\limits_{i = 0}^{n - 1}{C_iC_{n-i-1}x^n(n\geq 2)} \\ &= 1 + \sum\limits_{n\geq 1}\sum\limits_{i = 0}^{n - 1}C_i x^i C_{n - i - 1}x^{n - i - 1}x \\ &= 1 + x\sum\limits_{i\geq 0}C_ix^i\sum\limits_{n\geq 0}C_nx^n\\ &= 1 + xH^2(x) \end{align*}\)
我们解这个方程可得:
\(H(x) = \frac{1\pm \sqrt{1 - 4x}}{2x}\)。
我们需要选择哪一个根呢。
我们进行分子有理化:
\(H(x) = \frac{2}{1\pm \sqrt{1 - 4x}}\)。
我们发现当我们选择\(\frac{2}{1 - \sqrt{1 - 4x}}\)时,代入\(x = 0\)则会发现\(H(0) = 0\)的条件不符合的情况。
所以我们选择\(H(x) = \frac{1 + \sqrt{1 - 4x}}{2x}\)。
但我们发现卡特兰数和斐波那契的不同之处,这个\(H(x)\)的封闭形式,并不是一个多项式的形式。
所以我们考虑需要先展开 \(\sqrt{1 - 4x}\) :
我们使用二项式定理:
\(\begin{align*}
(1 - 4x) ^ {\frac{1}{2}} &= \sum\limits_{n\geq 0}\binom{\frac{1}{2}}{n}(-4x)^n \\
&= 1 + \sum\limits_{n\geq 1}\frac{(\frac{1}{2}^ \underline{n})}{n!}(-4x)^n \\
\end{align*}\)
我们有\((\frac{1}{2})^\underline{n} = \frac{(-1)^{n -1}\ \ (2n - 2)!}{2^{2n - 1}\ \ (n - 1)!}\)。
由于这个柿子的化简并不是我们讨论的主要内容,有需要可以转:化简过程。
我们把这个柿子带回原柿子,直接化简可以得到:
\((1-4x)^{\frac{1}{2}} = 1 + \sum\limits_{n \geq 1}{\binom{2n-1}{n}\frac{1}{2n - 1}2x^n}\)。
再带回原柿子。
\(H(x) = \sum\limits_{n\geq 0}\binom{2n}{n}\frac{1}{n + 1}x^n\)。
于是我们得到了通项。
\([x^n]H(x) = \frac{1}{n + 1}\binom{2n}{n}\)。
我们可以在 \(O(n)\) 次预处理的情况下,\(O(1)\) 回答一个询问。
例题
[SCOI2010]生成字符串
我们考虑到其实这个任意前缀 1 的个数都小于前缀 0 的个数,实际上和我们的在二维平面上游走不穿过 \(y = x\) 这条线的条件是等价的。
那么我们可以把题目转变为从 \((0,0)\) 走到 \((n,m)\) 处,不穿过 \(y = x\) 这条直线的方案数。
依照上面我们所做的翻转理论,其实即翻转完的终点变换为了 \((m - 1,n + 1)\) 。
所以答案为 \(\binom{n + m}{n} - \binom{n + m}{m - 1}\)。
#include<iostream>
#include<cstdio>
#define ll long long
#define N 1000005
#define mod 20100403
ll s[N << 1],inv[N << 1];
inline ll pow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1)ans = a * ans % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
inline ll C(ll x,ll y){
return s[x] * inv[y] % mod * inv[x - y] % mod;
}
int main(){
ll n,m;
scanf("%lld%lld",&n,&m);
s[0] = 1;
for(int i = 1;i <= n + m;++i)
s[i] = s[i - 1] * i % mod;
inv[n + m] = pow(s[n + m],mod - 2);
for(int i = n + m - 1;i >= 0;--i)
inv[i] = inv[i + 1] * (i + 1) % mod;
std::cout<<(C(n + m,n) - C(n + m,m - 1) + mod) % mod<<std::endl;
}
[AHOI2012]树屋阶梯
求用 \(n\) 个任意大小的矩形,覆盖高度为 \(n\) 的阶梯的方案数。
我们思考强制使用 \(n\) 个这个矩形的条件能够转化成什么对我们有利的条件:
我们在左下角这个矩形,一定右上角是某个拐点,否则我们会发现,我们需要额外使用一个矩形去覆盖这个拐点,\(n\) 个拐点对应 \(n\) 个矩形,那么这样最少也需要 \(n + 1\) 个。
那么我们就有了一个可以缩小问题规模的方案。
我们每次对这个阶梯状物,进行一个枚举覆盖左下角这个矩形的右上角是哪一个拐点,不妨设为从上到下第 \(x\) 个。
所以这个矩形上方有一个 \(x - 1\) 阶状物需要覆盖,右边有一个 \(n - x\) 阶状物需要处理。
所以答案为 \(C_n = \sum\limits_{i = 0}^{n -1}{C_iC_{n - i - 1}}\) 即 卡特兰数。
a=input()
c=1
for num in range (a+2,a*2+1):
c=c*num
for num in range (1,a+1):
c=c/num
print (c)
[TJOI2015]概率论
我们考虑期望的典型操作:
我们统计所有的可能出现的二叉树的数量 \(f_n\),以及所有二叉树的叶子总个数 \(g_n\)。
那么我们考虑前者,我们枚举根节点左儿子的数量可以知道 \(f_n = \sum\limits_{i = 0}^{n - 1}{f_if_{n - i - 1}}\) 即卡特兰数。
那么后面这个 \(g_n\) 怎么计算呢。(考虑打表并猜测并证明)。
\(g_n = nf_{n - 1}\)
考虑证明。
我们思考一颗 \(n\) 元树,有 \(k\) 个叶子节点,那么我们把这个 \(k\) 个叶子分别去掉,都会得到一颗 \(n - 1\) 元树,我们称得到的 \(n - 1\) 元树 \(\alpha\) 做了一次贡献。
那么我们只要对所有的 \(\alpha\) 的贡献之和就行了。
那么我们思考一下有多少个位置可以给我们放一个新的叶子节点获得一个 \(n\) 元树 \(\beta\)。
我们从度数角度考虑:
添加一个叶子后, \(dep(\beta) = dep(\alpha) + 1\) 。
一颗 \(\alpha\) 有 \(n - 1\)个点,其度数显然为 \(2(n - 2)\)。
我们把其所有叶子部位都补上,则有这 \(n - 1\) 个点的度数为 \(3(n - 2) + n - 2\),即除了根节点是 2 度,其他点都是 3 度,每添一个叶子节点,度数只会增加 1 ,所以能添 \(n\) 个叶子节点。
所以有 \(g_n = n * f_{n - 1}\)。
所以直接计算答案 \(\frac{n * f_{n - 1}}{f_n} = \frac{n(n + 1)}{2(2n - 1)}\)。
#include <cstdio>
int main() {
double n;
scanf("%lf", &n);
printf("%.12f", n * (n + 1) / (2 * (2 * n - 1)));
return 0;
}
[NOI2018] 冒泡排序
我们考虑转化条件:
好排列等同于序列中不存在一个长度大于等于 \(3\) 的下降子序列。
首先考虑排列如何达到交换下界。
单独考虑排列的一个数,对于其目标位置,我们知道他一定往目标去,那么对于排列\(2,1\),\(2\)要到后面,\(1\)要到前面,所以交换不会浪费次数。
但是如果 \(a_i,a_j,a_k(a_i > a_j > a_k)\) 那么 \(a_i\) 到后面,和\(a_k\) 到前面,中间 \(a_j\) 会浪费次数。
我们考虑当我们忽略字典序条件我们怎么做呢。
我们设 \(f_{i,j}\),为选了 \(i\) 个数,最大值为 \(j\) 的方案数,所以我们要么选一个更大的,要么选一个小的。
我们考虑不能出现三元以上的下降。
所以我们转移为:
\(f_{i,j} = \sum\limits_{j}^{k=i - 1}f_{i - 1,k}\)。
我们可以推出\(f_{i,j} = f_{i - 1,j} + f_{i,j - 1}(j \leq i)\)。
那么又转化为了平面游走问题。
我们有\(f_{i,j} = \binom{i + j}{i} - \binom{i + j}{j + 1}\)。
那么我们怎么处理字典序问题呢。
我们枚举位置 \(i\) ,前面的都和 \(p\) 相同,第 \(i\) 个数大于\(p_i\),然后将方案数加起来。
令 \(mx = \max\limits_{j = 1}^{i - 1}{p_j},mi\) 为当前最小的可以填的数。
那么我们重新定义 \(f_{i,j}\) 为从 \((i,j) \to (n,n)\) 的方案数,这里可以理解为我们定义 \(f_{i,j}\) 转为定义了前 \(i\) 个数 \(mx = j\),后面 \(n - j\) 个数填的方案数,可以看做是对于二元 \(f\) 做了一个后缀和,建议读者结合二维平面思考。
- 如果 \(p_i\) = \(mi\),显然我们只能填 \(x > mx\) 的数方案:\(f(i,mx + 1)\)。
- 如果 \(mi < p_i < mx\) ,显然我们只能填 \(x > mx\) 的数,但我们思考这样一定会有\(mx,p_i,mi\)的一个三元序列,所以此时无解。
- 如果\(p_i \geq mx\),我们填一个 \(x > p_i\)的数,那么方案数 \(f(i,p_i + 1)\)。
#include<iostream>
#include<cstdio>
#define ll long long
#define N 2000005
#define mod 998244353
ll s[N << 1 + 5],inv[N << 1 + 5];
inline ll pow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1)ans = a * ans % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
inline ll C(ll x,ll y){
return s[x] * inv[y] % mod * inv[x - y] % mod;
}
ll n,p[N];
ll T;
bool in[N];
ll fi(ll x,ll y){
if(x > y || y > n)return 0;
return (C((n << 1) - x - y,n - x) - C((n << 1) - x - y,n - x + 1) % mod + mod) % mod;
}
inline void solve(){
scanf("%lld",&n);
for(int i = 1;i <= n;++i)
scanf("%lld",&p[i]),in[i] = 0;
ll mx = 0,mi = 1,ans = 0;
for(int i = 1;i <= n;++i){
mx = std::max(mx,p[i]);
ans = (ans + fi(i - 1,mx + 1)) % mod;
in[p[i]] = 1;
while(in[mi])mi ++ ;
if(mi < p[i] && p[i] < mx)break;
}
std::cout<<ans<<std::endl;
}
int main(){
s[0] = 1;
for(int i = 1;i <= N << 1;++i)
s[i] = s[i - 1] * i % mod;
inv[N << 1] = pow(s[N << 1],mod - 2);
for(int i = (N << 1) - 1;i >= 0;--i)
inv[i] = inv[i + 1] * (i + 1) % mod;
scanf("%lld",&T);
while(T -- ){
solve();
}
}
总结
本文旨在带领读者发现一些在卡特兰数列中蕴含的内在,从这么多例题来看,卡特兰数数列本身并没有多少可扩展之物,其也很容易从打表暴力等方式看出来,但在其推导过程中的关键思想:容斥,通过某种操作缩小问题规模,找到关键性质,将一个抽象问题转化为几何问题对我们仍有启发意义,我们更应该关注的是在数列背后的一些乐趣,而非单纯用打表法做出题目。


