笛卡尔树学习指南
前言:感觉笛卡尔树这个东西特别神奇。
嗯。啥题都要笛卡尔树。嗯。
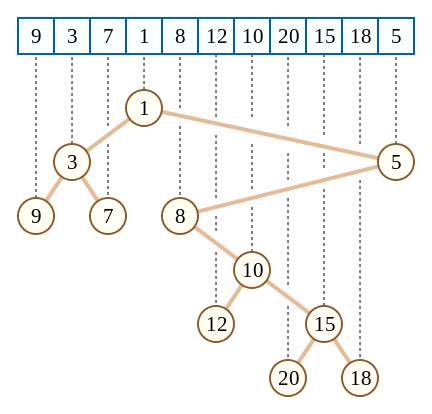
笛卡尔树是这样的一种结构。
每个树节点具有一对键值\((x,y)\),在笛卡尔树上,\(x\)以二叉搜索树的形式,\(y\)以堆的形式存在。
所以\(treap\)也是一种笛卡尔树。
建树方法。
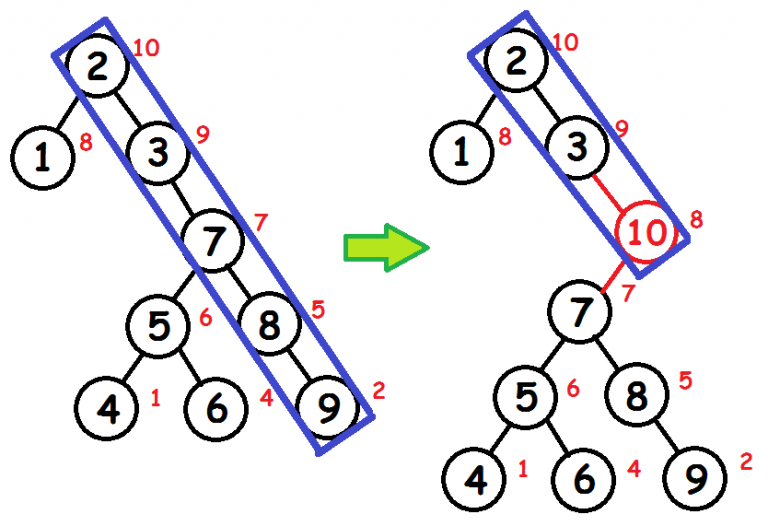
其中黑色的为\(x\),红色为\(y\).
我们考虑先对所有\(x\)点进行排序,考虑逐个插入。
由于需要保证二叉搜索树的性质,所以我们需要尽量把后一个点插入到前一个点的右侧。
那么我们考虑维护一条目前所插入的树结构的最右侧的链,用单调栈维护即可。
build
inline void in(int x){
ll last = 0;
while(p[stack[top]] > p[x] && top > 0)
last = stack[top],top -= 1;
if(top)
r[stack[top]] = x;
if(last)
l[x] = last;
stack[++top] = x;
}
for(int i = 1;i <= n;++i)
in(i); //按照x排序,in函数中p即为y值
例题
模板
因为本题里的\(x\)即为序号,所以在\(O(n)\)里可以解决这个问题。
模板
#include<iostream>
#include<cstdio>
#define ll long long
#define N 10000005
ll n;
ll p[N];
ll stack[N],top;//单调栈。
ll l[N],r[N];
inline void in(int x){
ll last = 0;
while(p[stack[top]] > p[x] && top > 0)
last = stack[top],top -= 1;
if(top)
r[stack[top]] = x;
if(last)
l[x] = last;
stack[++top] = x;
}
inline ll read(){
ll ans = 0,f = 1;
char a = getchar();
while(!(a == '-' || (a <= '9' && a >= '0')))
a = getchar();
while(a <= '9' && a >= '0')
ans = (ans << 3) + (ans << 1) + (a - '0'),a = getchar();
return ans;
}
int main(){
n = read();
for(int i = 1;i <= n;++i)
p[i] = read();
for(int i = 1;i <= n;++i)
in(i);
ll ans = 0;
for(int i = 1;i <= n;++i)
ans ^= i * (l[i] + 1);
std::cout<<ans<<" ";
ans = 0;
for(int i = 1;i <= n;++i)
ans ^= i * (r[i] + 1);
std::cout<<ans<<"";
}
应用
那笛卡尔树能用来干啥啊,啥都不行我学他干嘛。
查询序列中一段以\(a[i]\)为最大值/最小值的连续区间长度,即他在笛卡尔树中的子树大小。
Largest Rectangle in a Histogram
Largest Rectangle in a Histogram
#include<iostream>
#include<cstdio>
#define ll long long
#define N 100005
ll n,p[N];
ll stack[N],top;//单调栈。
ll l[N],r[N],siz[N],f[N];
inline void in(int x){
ll last = 0;
while(p[stack[top]] > p[x] && top > 0)
last = stack[top],top -= 1;
if(top)
r[stack[top]] = x,f[x] = stack[top];
if(last)
l[x] = last,f[last] = x;
stack[++top] = x;
}
ll ans;
inline void clear(){
ans = 0;
top = 0;
for(int i = 1;i <= n;++i)
siz[i] = 0,stack[i] = 0,l[i] = r[i] = 0,f[i] = 0;
}
inline void dfs(int u){
siz[u] = 1;
if(l[u])
dfs(l[u]),siz[u] += siz[l[u]];
if(r[u])
dfs(r[u]),siz[u] += siz[r[u]];
// std::cout<<u<<" "<<u<<" "<<siz[u]<<std::endl;
ans = std::max(ans,siz[u] * p[u]);
}
int main(){
while(scanf("%lld",&n) && n != 0){
for(int i = 1;i <= n;++i)
scanf("%lld",&p[i]);
for(int i = 1;i <= n;++i)
in(i);
ll root = 0;
for(int i = 1;i <= n;++i){
// std::cout<<l[i]<<" "<<r[i]<<std::endl;
if(!f[i]){
root = i;
break;
}
}
dfs(root);
std::cout<<ans<<std::endl;
clear();
}
}
笛卡尔树上的分治问题
笛卡尔树对于和区间\(max/min\)有关的问题上,具有很不错的性质。
Beautiful Pair
考虑分治一下.
Beautiful Pair
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int q[100010];
int ll[100010],rr[100010],top,root;
inline void build(long long a[],int n)
{
int maxn=-0x3f3f3f3f;
for(int i=1;i<=n;i++)
{
if(a[i]>maxn)
{
root=i;
maxn=a[i];
}
while(!top==0&&a[q[top-1]]<a[i])
{
ll[i]=q[top-1];
top--;
}
if(!top==0)
{
rr[q[top-1]]=i;
}
q[top++]=i;
}
}
int n,size;
long long a[100010],c[100010],b[100010],ans;
inline void add(int x,long long v)
{
for(;x<=n;x+=(x&-x)) c[x]+=v;
}
inline long long query(int x)
{
long long ans=0;
for(;x;x-=(x&-x)) ans+=c[x];
return ans;
}
inline void dfs(int u,int l,int r)
{
if(u==0) return ;
if(u-l>r-u)
{
for(int i=u;i<=r;i++)
{
int now=upper_bound(b,b+size+1,b[a[u]]/b[a[i]])-b;
if(now) ans-=query(now-1);
}
dfs(ll[u],l,u-1);
add(a[u],1);
for(int i=u;i<=r;i++)
{
int now=upper_bound(b,b+size+1,b[a[u]]/b[a[i]])-b;
if(now) ans+=query(now-1);
}
dfs(rr[u],u+1,r);
}
else
{
for(int i=l;i<=u;i++)
{
int now=upper_bound(b,b+size+1,b[a[u]]/b[a[i]])-b;
if(now) ans-=query(now-1);
}
dfs(rr[u],u+1,r);
add(a[u],1);
for(int i=l;i<=u;i++)
{
int now=upper_bound(b,b+size+1,b[a[u]]/b[a[i]])-b;
if(now) ans+=query(now-1);
}
dfs(ll[u],l,u-1);
}
}
/*
这个地方的树状数组如果单层都要暴力然后删除的话就会挂,因为复杂度就不能保证
所以考虑中序遍历,加入贡献。可以发现,如果之前树状数组有的数,就可以在进入的时候消除影响,左子树上来的时候再记录。然后再通过小区间查询,就可以保证复杂度
*/
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b+1,b+n+1);
size=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+size+1,a[i])-b;
build(a,n);
dfs(root,1,n);
printf("%lld\n",ans);
}
维护分段函数
暂时鸽一下。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号