模拟退火学习笔记

模拟退火解决下面这种问题：
对于一类求最值的问题（默认为最小值，最大值也可以），其合法的方案的状态数有很多甚至于无穷。
无法用搜索满足，而且对一个合法方案来说，容易从他构造出另一个合法方案。

考虑对于合法方案的值的图像。

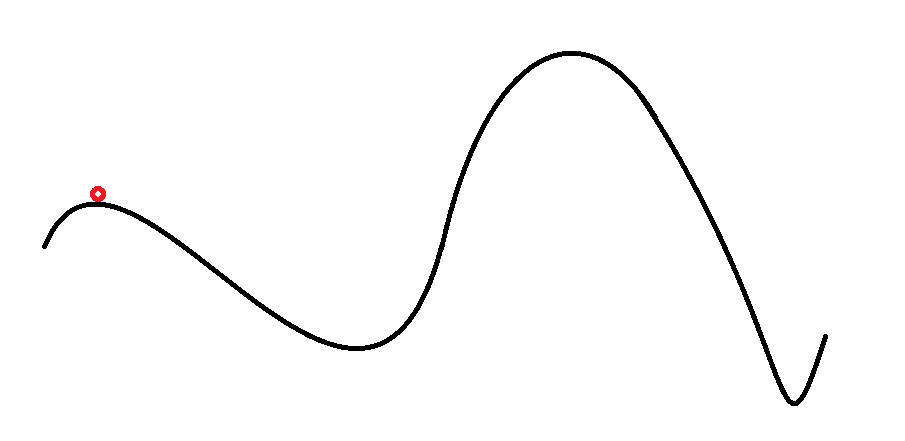
我们考虑从一个起始态，向离他最近的局部最优点靠近。

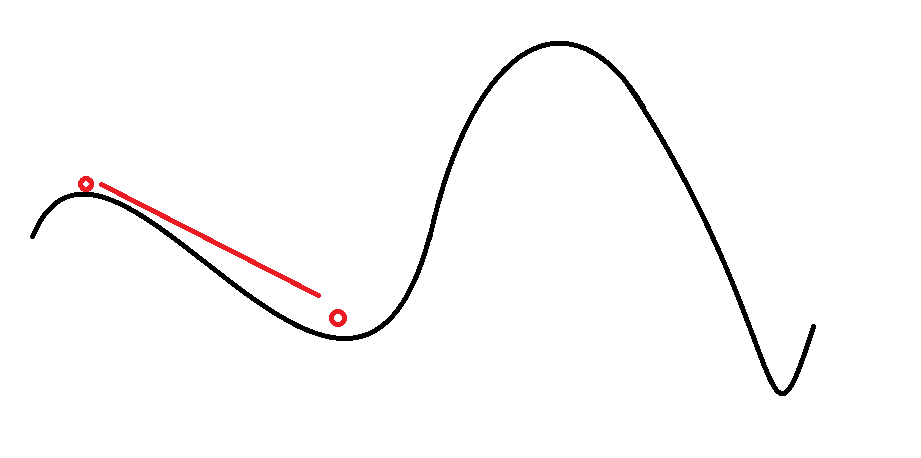
但我们发现局部最优并非全局最优

为了解决这一问题，科学家们想到了物理的退火降温的过程——

一个处于很高温度的物体，现在要给它降温，使物体内能降到最低。

我们常规的思维是，越快越好，让它的温度迅速地降低。

然而，实际上，过快地降温使得物体来不及有序地收缩，难以形成结晶。而结晶态，才是物体真正内能降到最低的形态。

正确的做法，是徐徐降温，也就是退火，才能使得物体的每一个粒子都有足够的时间找到自己的最佳位置并紧密有序地排列。开始温度高的时候，粒子活跃地运动并逐渐找到一个合适的状态。在这过程中温度也会越降越低，温度低下来了，那么粒子也渐渐稳定下来，相较于以前不那么活跃了。这时候就可以慢慢形成最终稳定的结晶态了。

那么，我们可不可以把找到最优解，与形成结晶态，这两个过程联系在一起呢？

于是，模拟退火诞生了。（以上摘抄于模拟退火）

我们考虑这么几个参数。

\(T\):当前温度
\(end\):结束温度
\(p\)：温度下降曲率
\(f(x)\)：当前方案的值
\(f(y)\)：新方案的值
\(z\):差值

我们考虑如果\(z < 0\)则把\(y\)作为下次迭代的方案。
否则我们为了让这个方案不局限在一个凹面里，我们需要一个概率让他跳出这个凹。
这个概率是\(exp(-z / T) * RANDMAX\)（是的，模拟退火是一个随机算法）

像这样，就能够跳到最优解的位置
而且随着温度的下降，接受差解的概率越来越小，则该算法逐渐趋于稳定。

值得注意的是：
在过程中，并非最终态的值成为我们的答案，他只是一个逼近值，或者说应该是一个局部最优。
该算法是一个随机算法，我们需要在不断跳的过程中记录最小值作为最终答案。
调参的话，多做一些题。
在比赛中使用该算法，最好手动构造一些大数据。
并且不要想着拿满分。