【动态规划杂谈】
前言
最后一块了,这周写完就去板刷联合省选
单调队列
[POI2014]PTA-Little Bird
[POI2014]PTA-Little Bird
没什么好说的,决策单调性考虑一下就好了
#include<iostream>
#include<cstdio>
#define ll long long
#define N 2000000
ll n,q;
ll v[N];
ll QWQ[N],s,t,ans[N];
void del(ll k){
QWQ[1] = 1,ans[1] = 0;
s = 1,t = 1;
for(int i = 2;i <= n;++i){
ll l = std::max((ll)1,i - k);
while(QWQ[s] < l && (s <= t)){s ++;}
ans[i] = ans[QWQ[s]] + (v[i] >= v[QWQ[s]]);
while((ans[QWQ[t]] > ans[i] || (ans[QWQ[t]] == ans[i] && v[QWQ[t]] <= v[i])) && t >= s)
t -- ;
QWQ[++t] = i;
}
std::cout<<ans[n]<<std::endl;
}
int main(){
scanf("%lld",&n);
for(int i = 1;i <= n;++i)
scanf("%lld",&v[i]);
scanf("%lld",&q);
while(q -- ){
ll k;
scanf("%lld",&k);
del(k);
}
}
斜率优化
[SDOI2016]征途
[SDOI2016]征途
仔细的分析一下题目
其实要求的答案是这个
\(m\sum{x_i ^ 2} - (\sum{x_i}) ^ 2\)
此时我们显然只需要考虑使\(\sum{x_i^2}\)最小
设\(f_{i,j}\)为到第\(i\)个数,划分了\(j\)段的最小值,那么\(f_{i,j} = min(f_{k,j - 1} + (sum_i - sum_k) ^ 2)\)
看到后面这个柿子
自然看到了斜率优化
#include<iostream>
#include<cstdio>
#define ll long long
#define N 4000
ll n,m;
ll v[N],f[N][N],s[N];
ll head,end;
ll QWQ[N];
ll k;
inline ll a(ll x){return s[x];}
inline ll Y(ll x){return f[x][k - 1] + s[x] * s[x];}
inline ll X(ll x){return s[x];}
inline double solve(ll x,ll y){return (1.0 * Y(y) - Y(x)) / (1.0 * X(y) - X(x));}
int main(){
scanf("%lld%lld",&n,&m);
for(int i = 1;i <= n;++i)
scanf("%lld",&v[i]),s[i] = s[i - 1] + v[i];
for(int i = 1;i <= n;++i)
f[i][1] = s[i] * s[i];
for(k = 2;k <= m;++k){
head = end = 1;
QWQ[head] = 0;
for(int i = 1;i <= n;++i){
while(head < end && solve(QWQ[head],QWQ[head + 1]) < 2 * s[i]) ++ head;
f[i][k] = f[QWQ[head]][k - 1] + (s[i] - s[QWQ[head]]) * (s[i] - s[QWQ[head]]);
while(head < end && solve(QWQ[end - 1],QWQ[end]) > solve(QWQ[end],i))--end;
QWQ[++end] = i;
}
}
std::cout<<m * f[n][m] - s[n] * s[n]<<std::endl;
}
[JSOI2011] 柠檬
不太会,先鸽着,大概有一点想法就是两端的颜色一样,用颜色来计算。
决策单调性
[POI2011]Lightning Conductor
[POI2011]Lightning Conductor
这。。
是一道我看错题目,然后推到自闭的题
我疯狂推,发现了不存在单调性。。。。。
大概是这么个意思吧
求\(p_i = max(a_j - a_i + \sqrt{\vert(i - j)\vert)\)
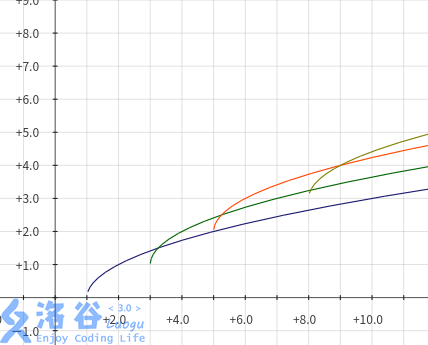 (借一下你谷神仙的图)
(借一下你谷神仙的图)
我们看到,其实如果我们考虑从前往后,从后往前,那么我们不用考虑绝对值。
那我们只考虑从前往后,那么对于每个点决策我们发现,必定是单调上升的。
所以我们可以利用这个方法进行分治处理。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 5;
int n, a[maxn]; double ans[maxn];
double calc(int i, int j) {
return a[j] - a[i] + sqrt((double)i - j);
}
void solve(int l, int r, int jl, int jr)
{
int m = l + r >> 1;
int jp = jl; double jval = calc(m, jl), val;
for (int j = jl; j <= jr && j <= m; j++) {
val = calc(m, j);
if (val > jval) jval = val, jp = j;
}
ans[m] = max(ans[m], jval);
if (l < m) solve(l, m - 1, jl, jp);
if (m < r) solve(m + 1, r, jp, jr);
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
solve(1, n, 1, n);
reverse(a + 1, a + n + 1);
reverse(ans + 1, ans + n + 1);
solve(1, n, 1, n);
for (int i = n; i >= 1; i--) printf("%d\n", (int)ceil(ans[i]));
return 0;
}
数据结构维护
[HEOI2016/TJOI2016]序列
[HEOI2016/TJOI2016]序列
\(DP\)柿子不再赘述,发现是一个三维偏序的转移,\(CDQ\)分治和各种嵌套数据结构都行,现在才发现,自己嵌套数据结构和可持久化可能跟没有学过一样
借一下兔兔的\(CDQ\)代码
我会补上的
#include <cstdio>
#include <algorithm>
using namespace std;
const int MN = 100005;
const int MC = 100000;
int N, M;
int A[MN], Mx[MN], Mn[MN];
int f[MN], Ans;
int p[MN];
inline bool cmp1(int i, int j) { return Mx[i] < Mx[j]; }
inline bool cmp2(int i, int j) { return A[i] < A[j]; }
int B[MN];
inline void Ins(int i, int x) { for (; i <= MC; i += i & -i) B[i] = max(B[i], x); }
inline void Clr(int i) { for (; i <= MC; i += i & -i) B[i] = 0; }
inline int Qur(int i) { int A = 0; for (; i; i -= i & -i) A = max(A, B[i]); return A;}
void CDQ(int lb, int rb) {
if (lb == rb) {
f[lb] = max(f[lb], 1);
return;
}
int mid = lb + rb >> 1;
CDQ(lb, mid);
for (int i = lb; i <= rb; ++i)
p[i] = i;
sort(p + lb, p + mid + 1, cmp1);
sort(p + mid + 1, p + rb + 1, cmp2);
int j = lb;
for (int i = mid + 1; i <= rb; ++i) {
while (j <= mid && Mx[p[j]] <= A[p[i]]) {
Ins(A[p[j]], f[p[j]]);
++j;
}
f[p[i]] = max(f[p[i]], Qur(Mn[p[i]]) + 1);
}
for (int i = lb; i <= mid; ++i)
Clr(A[i]);
CDQ(mid + 1, rb);
}
int main() {
int x, y;
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i)
scanf("%d", &A[i]),
Mx[i] = Mn[i] = A[i];
for (int i = 1; i <= M; ++i)
scanf("%d%d", &x, &y),
Mx[x] = max(Mx[x], y),
Mn[x] = min(Mn[x], y);
CDQ(1, N);
for (int i = 1; i <= N; ++i)
Ans = max(Ans, f[i]);
printf("%d\n", Ans);
return 0;
}



