浅谈KMP算法

有关的一些解释

下面的阐述中使用next只是方便理解 请不要在代码中使用next作为数组名（如果你用using namespace std的话）

用来解决的问题：

在比较字符串A和B中询问B中是否包含A

算法

我们将A和B字符串都从第一位开始编号
我们定义一个\(next_i\)的值
其含义是满足A[\(1\)~\(next_i\)] = A[\(i - next_i + 1\)~\(i\)]且\(next_i\)最大 自然 \(next_i \neq i\)

例子

、

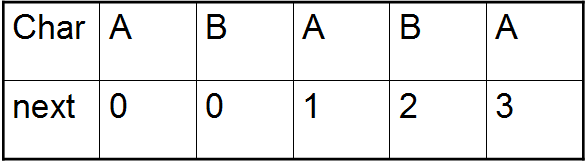求法

我们思考 假如我们已经知道了next[1~i-1] 我们怎么求 next[i]呢
我们让A[next[i - 1] + 1] 同 A[i] 比较 如果相等 那么 next[i] = next[i - 1] + 1
否则
我们让A[next[next[i - 1]] + 1] 同 A[i] 比较 如果相等 那么 next[i] = next[next[i - 1]] + 1
大家可以自己思考这样的正确性
我们重复这个过程 就可以求出 next[1~n]

代码

    nex[1] = 0;
    ll n = strlen(a + 1);
    ll m = strlen(b + 1);
    for(ll i = 2,j = 0;i <= n;i++)
    {
    	while(j > 0 && a[i] != a[j + 1]) j = nex[j];
    	if(a[i] == a[j + 1]) j++;
    	nex[i] = j;
    }

比较B和A

我们定义f[i]同next[i]相似
其含义是满足A[\(1\)~\(f_i\)] = B[\(i - f_i + 1\)~\(i\)]且\(f_i\)最大 自然 \(f_i \neq i\)
因为定义的相似性
那么可以知道它们的求法没有多大差别

代码

	for(ll i = 1,j = 0;i <= m;i++)
	{
		while(j > 0&& (j == n || b[i] != a[j + 1])) j = next[j];
		if(b[i] == a[j + 1]) j ++;
		f[i] = j;
		if(f[i] == n) 
		cout<<i<<endl;//此时A在B中出现一次 
	}

完整代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long 
using namespace std;
char a[10000],b[10000];
ll nex[10000],f[10000];
int main()
{
	cin>>a + 1;
	cin>>b + 1;
	nex[1] = 0;
    ll n = strlen(a + 1);
    ll m = strlen(b + 1);
    for(ll i = 2,j = 0;i <= n;i++)
    {
    	while(j > 0 && a[i] != a[j + 1]) j = nex[j];
    	if(a[i] == a[j + 1]) j++;
    	nex[i] = j;
	}
	/*for(ll i = 1;i <= n;i++)
	cout<<nex[i]<<endl;*/
	for(ll i = 1,j = 0;i <= m;i++)
	{
		while(j > 0&& (j == n || b[i] != a[j + 1])) j = nex[j];
		if(b[i] == a[j + 1]) j ++;
		f[i] = j;
		if(f[i] == n) 
		cout<<i<<endl;//此时A在B中出现一次 
	}
}