【CTSC1999】【带权并查集 】月亮之眼

Description

　　吉儿是一家古董店的老板娘，由于她经营有道，小店开得红红火火。昨天，吉儿无意之中得到了散落民间几百年的珍宝—月亮之眼。吉儿深知“月亮之眼”价值连城：它是由许多珍珠相连而成的，工匠们用金线连接珍珠，每根金线连接两个珍珠；同时又对每根金线染上两种颜色，一半染成银白色，一半染成黛黑色。由于吉儿自小熟读古籍，所以还晓得“月亮之眼”的神秘传说：“月亮之眼”原是一个古代寺庙的宝物，原本是挂在佛堂的一根顶梁柱上的，整个宝物垂直悬挂，所有珍珠排成一线，且都镶嵌在柱子里，而每一根金线又都是绷紧的，并且金线的银白色一端始终在黛黑色一端的上方；然而，在一个月圆之夜，“月亮之眼”突然从柱里飞出，掉落下来，宝物本身完好无损，只是僧侣们再也无法以原样把“月亮之眼”嵌入柱子中了。吉儿望着这个神秘的宝物，回忆着童年读到的传说，顿时萌发出恢复“月亮之眼”的冲动，但是摆弄了几天依旧没有成功。
　　现在，要麻烦您来帮助吉儿完成这项使命。
　　您要设计一个程序，对于给定的“月亮之眼”进行周密分析，然后给出这串宝物几百年前嵌在佛堂顶梁柱上的排列模样。给定的“月亮之眼”有N个珍珠和P根金线，所有珍珠按一定顺序有了一个序号：1、2…、N。

Input

输入数据包含一个“月亮之眼”的特征描述：
文件第一行有两个整数N和P，其中N表示宝物中的珍珠个数，P表示宝物中的金线根数；
以下P行描述珍珠连接情况：
文件第I+1行有三个整数，Ri1,Ri2,Li。其中Ri1表示第I根金线的银白色一端连接的珍珠序号；Ri2表示第I根金线的黛黑色一端连接的珍珠序号；Li表示第I根金线的长度。

Output

由于珍珠尺寸很小，所以几个珍珠可以同时镶嵌在一个位置上。
您的输出数据描述的是“月亮之眼”各个珍珠在顶梁柱上的位置，输出文件共N行：
第I行，一个整数S，它表示标号为I的珍珠在顶梁柱上距离最高位置珍珠的距离。
注意：若无解则输出仅一行，包含一个整数“-1”。

Sample Input

 

9 9
1 2 3
2 3 5
2 7 1
4 5 4
5 6 1
5 9 1
6 7 1
7 8 3
9 8 4

 

Sample Output

 

2
5
10
0
4
5
6
9
5

 

Hint

参数限定
1<=N<=255

样例说明：
我们把输入依次投射出来，从左到右，具体如下图：

 

题意有些难懂 但结合图片就不难理解了

因为输出只是离最高的珠子的的距离 我们考虑带权的并查集并采用路径压缩

 

对于一对珠子 X Ｙ X在Y上方 距离为Z 当XY不在同一并查集时

则有两种情况

 

 

 

 

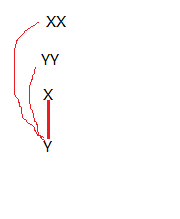
 一种在X并查集的树根XX到Ｙ的距离大于在Y的并查集的树根YY到Y的距离 （即在这条直线上 XX 高于 YY）

此时连接Ｘ——Ｙ　与 连接XX——YY同理  距离为 XX到Y距离去YY到Y的距离（d[x] + Ｚ - d[y]）

 同理 当YY高于XX也是同理      距离为 YY到Y距离去XX到Y的距离（-d[x] - S + d[y]）

 

 当XＹ在同一并查集时　则必有Ｘ　Ｙ　到树根距离为Ｚ　否则不能绷直或连线

贴代码

#include<iostream>
#include<cstdio>
#define LL long long
#define f(a,b) for(long long i = (a); i <= (b); i++)
using namespace std;
long long n,m,sum;
long long fa[1000],d[3000];
long long begin,final,value,x,y;
void merge(long long xx,long long yy,long long sum)
{
    fa[xx] = yy, d[xx] = sum;
}
long long  get(long long x)
{
    if(x == fa[x]) return x;
    long long root = get(fa[x]);
    d[x] += d[fa[x]];
    return fa[x] = root;
}
int main()
{
    scanf("%lld%lld",&n,&m);
    f(1,n)fa[i] = i,d[i] = 0;
    f(1,m) 
    {
      scanf("%lld%lld%lld",&x,&y,&value);
      long long x_father = get(x),y_father = get(y);
      if(x_father == y_father)
      if(d[y] - d[x] != value) 
      {
          cout<<-1;
        return 0;
      }
      if(d[x] + value >= d[y]) merge(y_father,x_father,d[x] + value - d[y]);
      if(d[x] + value < d[y]) merge(x_father,y_father,d[y] - value - d[x]);
    }
    f(1,n) 
    long long QWQ = get(i);
    f(1,n)cout << d[i]<<endl;
}