排序算法之计数排序

简介

        计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。

        它的优势在于在对一定范围内的整数排序时，它的复杂度为 \(O(n+k)\)（其中 k 是整数的范围），快于任何比较排序算法。

        当然这是一种牺牲空间换取时间的做法，而且当 \(O(k) > O(n\log_2 n)\) 的时候其效率反而不如基于比较的排序。

        基于比较的排序的时间复杂度在理论上的下限是 \(O(n\log_2 n)\)，如归并排序，堆排序等。

基本思想

        计数排序其主要思想是首先找到数据的 最大值 max 和 最小值 min，然后开辟一个长度为 max - min + 1 的计数数组，然后执行关键的两步：

        1、扫描一遍初始数组，以当前值 - min 作为下标，将该下标的计数器加1。

        2、然后扫描一遍计数器数组，按顺序把值收集起来。

        举个栗子， num =｛2, 1, 3, 1, 5｝。

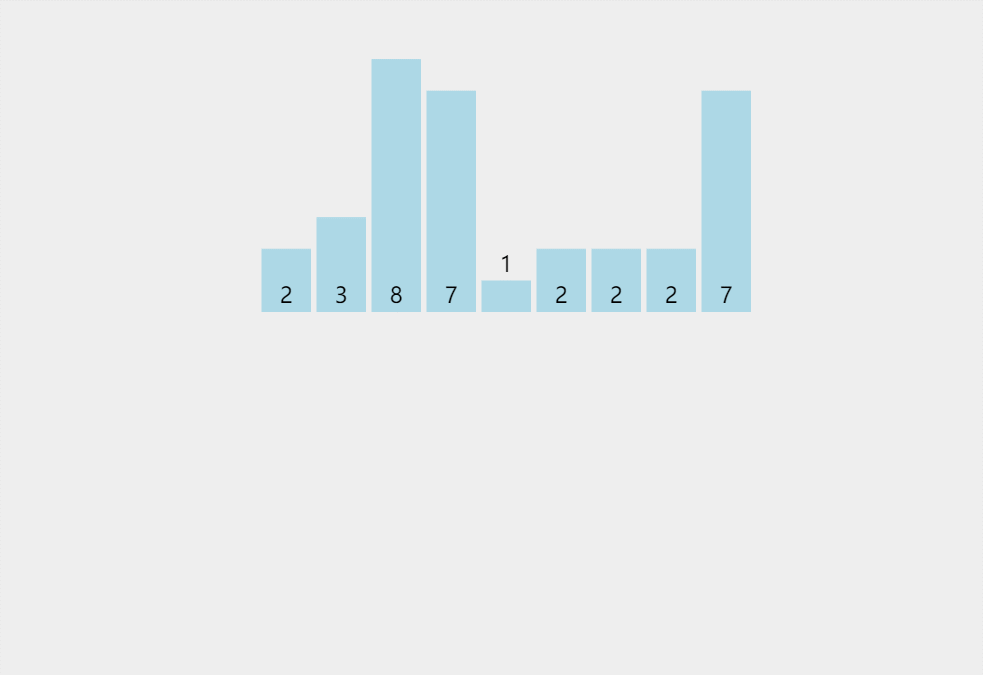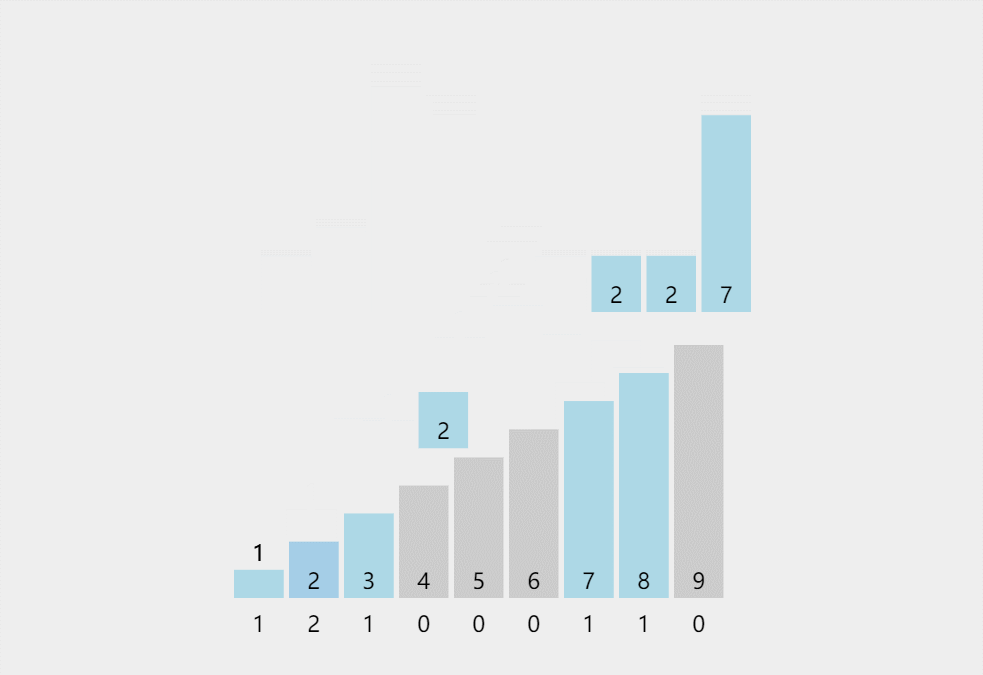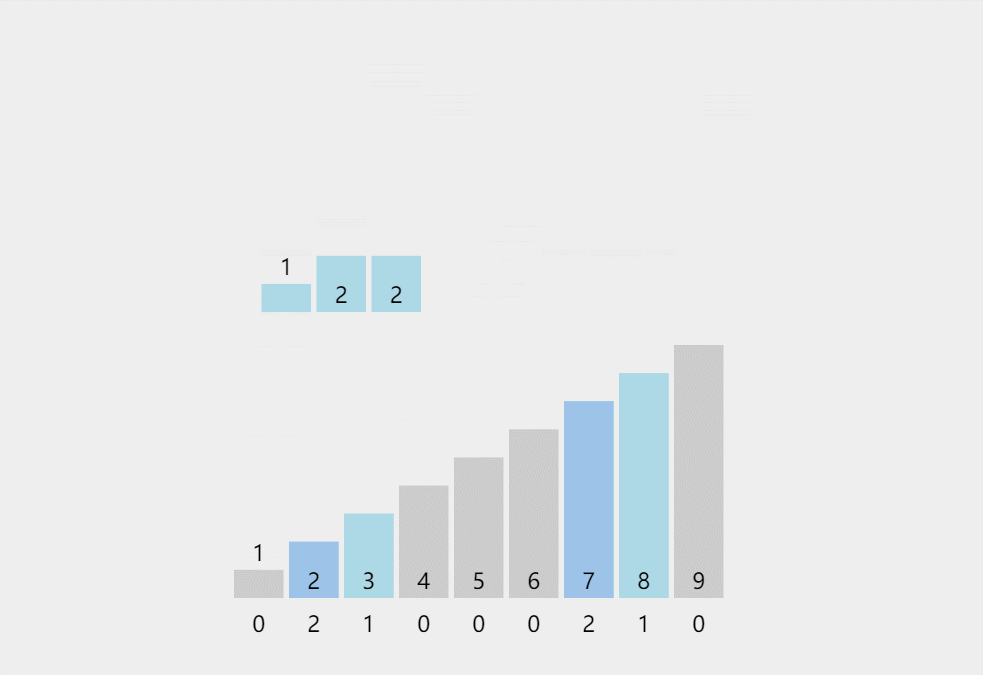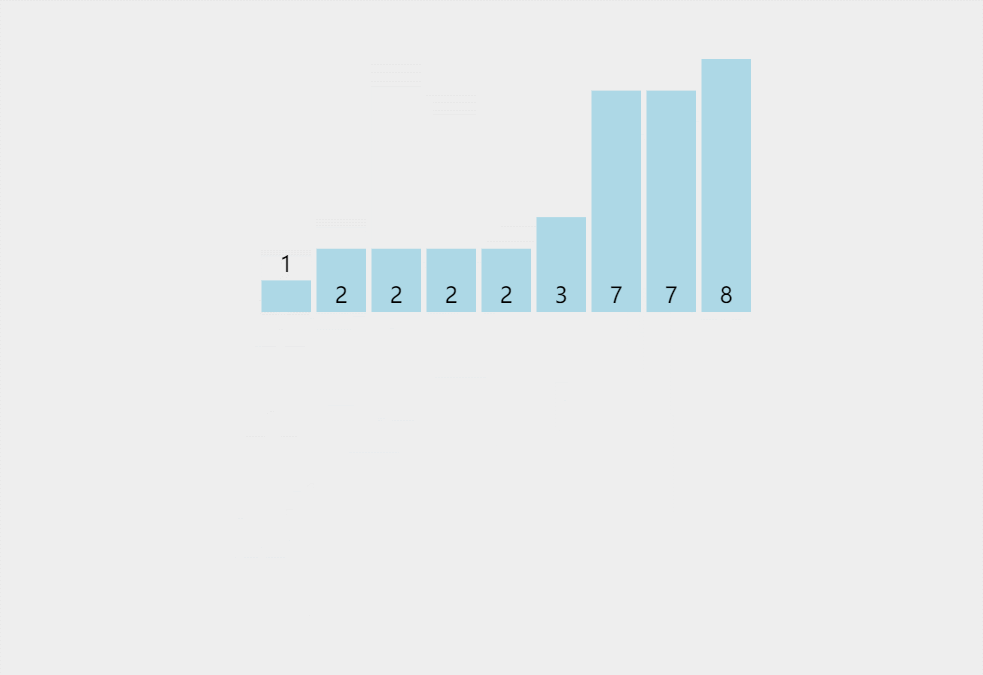
        首先扫描一遍获取最小值和最大值，max = 5，min = 1。于是开辟一个长度为5的计数器数组 count。

        1、统计每个元素出现的频率，得到 count = [2, 1, 1, 0, 1] ，例如 count[0] 就表示值 0 + min = 1 出现了2次。

        2、count[0] = 2 表示 1 出现了两次，那就向原始数组写入两个1；count[1] = 1 表示 2 出现了1次，那就向原始数组写入一个2。

        以此类推，最终原始数组变为｛1, 1, 2, 3, 5｝，排序完成。

排序过程

        此处排序数据：{2,3,8,7,1,2,2,2,7}

代码实现

/**
 * 计数排序
 * @Author distance
 */
public class CountSort {

    public static void sort(int[] num) {
        int max = Integer.MIN_VALUE , min = Integer.MAX_VALUE;
        for (int i = 0; i < num.length; i++) { // 找最大值和最小值
            if (num[i] > max) {
                max = num[i];
            }
            if (num[i] < min) {
                min = num[i];
            }
        }

        int k = max - min + 1;  // 长度
        int[] count = new int[k];
        for (int i = 0; i < num.length; i++) { // 统计
            count[num[i] - min] ++; // 偏移存储
        }

//        for (int i = 0; i < k; i++) {
//            System.out.println((i + min) + " => " + count[i]);
//        }

        int index = 0; // 下标
        for (int i = 0; i < k; i++) {
            while (count[i] > 0) {
                num[index ++] = i + min; // 偏移回来
                count[i] --;
            }
        }
    }

    public static void main(String[] args) {
        int[] num = {2,3,8,7,1,2,2,2,7};
        CountSort.sort(num);

        for (int i = 0; i < num.length; i++) {
            System.out.print(num[i] + " ");
        }
    }
}

算法分析

时间复杂度

        计数排序算法没有用到元素间的比较，它利用元素的实际值来确定它们在输出数组中的位置。因此，计数排序算法不是一个基于比较的排序算法，从而它的计算时间下界不再是 \(O(n\log_2 n)\)。

        另一方面，计数排序算法之所以能取得线性计算时间的上界，是因为对元素的取值范围作了一定限制，即 \(k = O(n)\)，k 是指整数的范围。如果 \(k=n^2,n^3 ...\) ，就得不到线性时间的上界。

        所以计数排序的时间复杂度为 O(n + k)。

算法稳定性

        此外，我们看到，由于算法经计数排序，输出序列中值相同的元素之间的相对次序与他们在输入序列中的相对次序相同。

        所以计数排序是一种稳定排序算法。