排序算法之快速排序

简介

        快速排序（QuickSort）是对冒泡排序算法的一种改进。

        快速排序通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

基本思想

        快速排序算法通过多次比较和交换来实现排序。

        （1）首先设定一个分界值，通过该分界值将数组分成左右两部分。

        （2）将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。

                此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

        （3）然后，左边和右边的数据可以独立排序。

                对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。

                右侧的数组数据也可以做类似处理。

        （4）重复上述过程，可以看出，这是一个递归定义。

                通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。

                当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

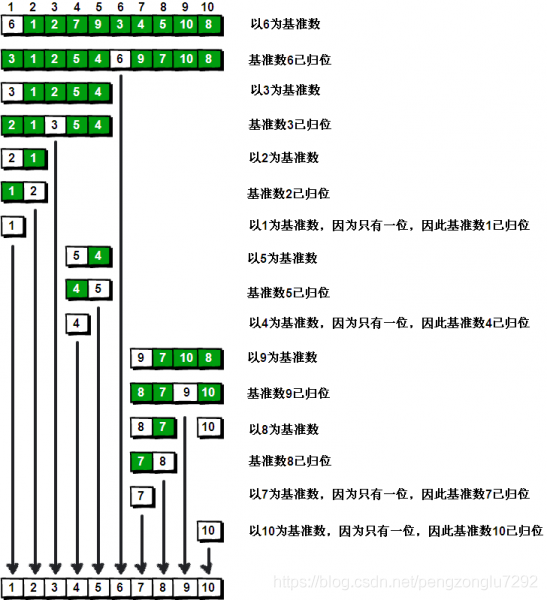
（图片参考：https://blog.csdn.net/pengzonglu7292/article/details/84938910）

排序过程

        此处排序数据：{5,3,7,6,4,1,2,9,10,8}

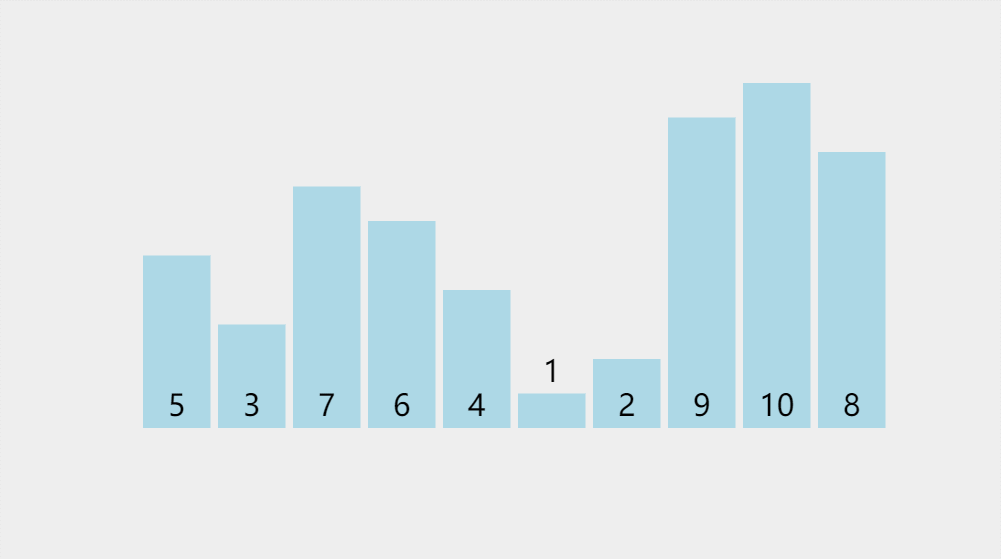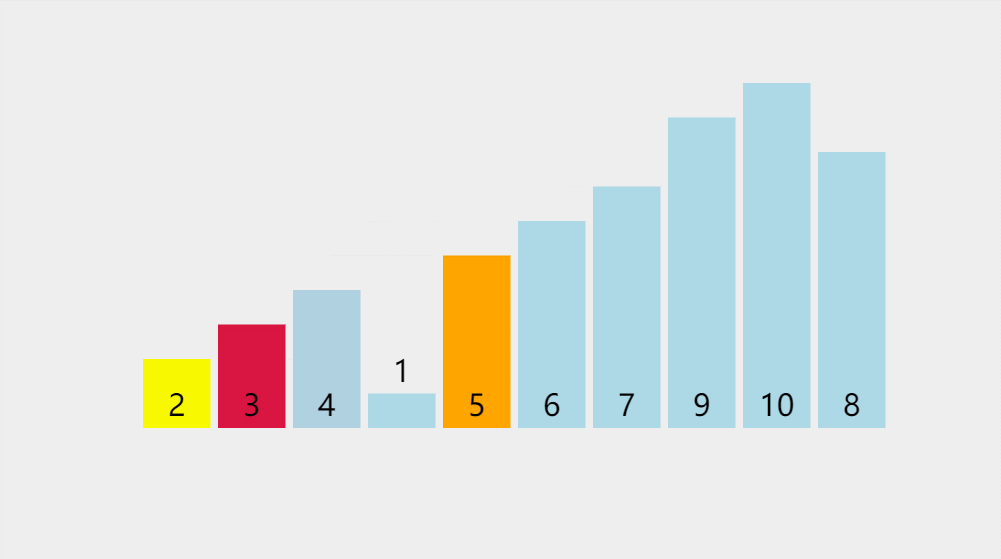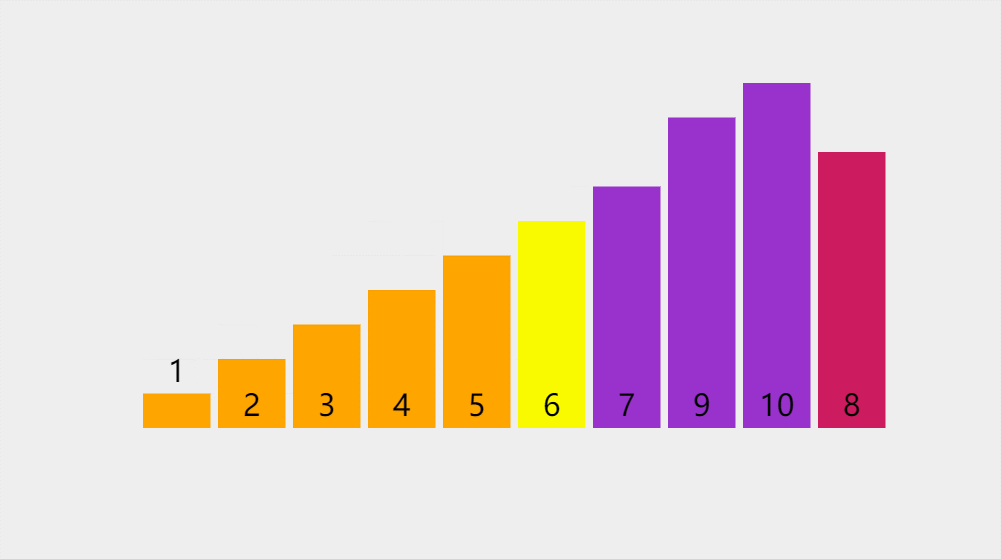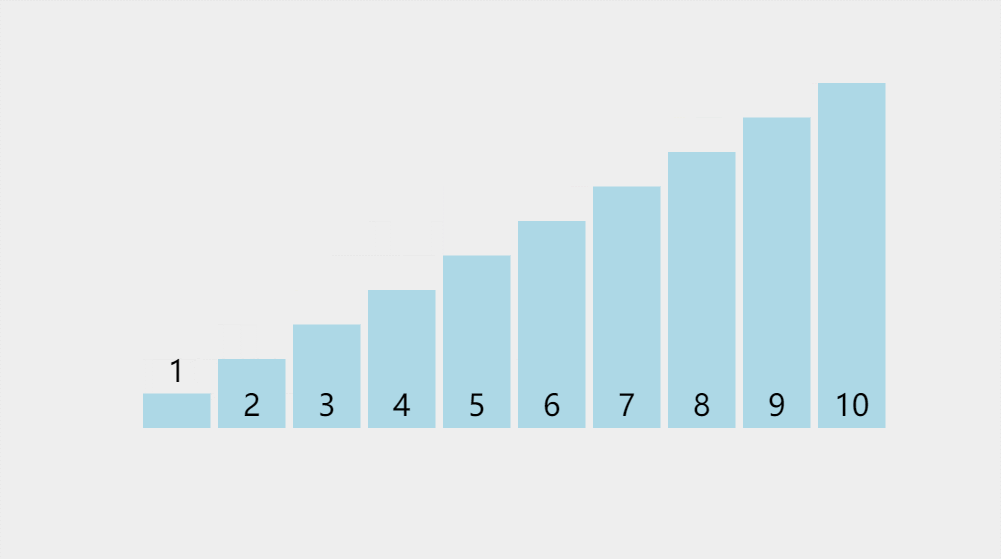
代码实现

/**
 * 快速排序
 * @Author distance
 */
public class QuickSort {

    public static void quickSort(int[] num, int left, int right) {
        if (left > right) {
            return;
        }

        int i = left, j = right;
        int key = num[left], temp; // 开始 left 位置作为基准值 

        while (i != j) {
            while (j > i && num[j] >= key) { // 从右往左找第一个小于 key 值的元素
                j --;
            }

            while (i < j && num[i] <= key) { // 从左往右找第一个大于 key 值的元素
                i ++;
            }

            if (i < j) {
                temp = num[i];
                num[i] = num[j];
                num[j] = temp;
            }
        }

        temp = num[left];  // 交换 left 位置和 i 位置的值，同时 i 位置作为基准值
        num[left] = num[i];
        num[i] = temp;

        quickSort(num, left, i - 1); // 递归对 i 左边快排
        quickSort(num, i+1, right); // 递归对 i 右边快排
    }

    public static void sort(int[] num) {

        quickSort(num, 0, num.length - 1);
    }

    public static void main(String[] args) {
        int[] num = {5,3,7,6,4,1,2,9,10,8};
        QuickSort.sort(num);

        for (int i = 0; i < num.length; i++) {
            System.out.print(num[i] + " ");
        }
    }
}

算法分析

时间复杂度

        快速排序的一次划分算法从两头交替搜索，直到low和hight重合，因此其时间复杂度是 \(O(n)\) ；而整个快速排序算法的时间复杂度与划分的趟数有关。

        理想的情况是，每次划分所选择的中间数恰好将当前序列几乎等分，经过 \(\log_2 n\) 趟划分，便可得到长度为1的子表。这样，整个算法的时间复杂度为 \(O(n\log_2 n)\) 。

        最坏的情况是，每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度-1。这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法的时间复杂度为 \(O(n^2)\)。

        为改善最坏情况下的时间性能，可采用其他方法选取中间数。通常采用“三者值取中”方法，即比较 num[left]、num[right] 和num[(left + right)/2]，取三者中关键字为中值的元素为中间数。

        可以证明，快速排序的平均时间复杂度也是 \(O(n\log_2 n)\)。因此，该排序方法被认为是目前最好的一种内部排序方法。

        所以快速排序的平均时间复杂度为 O(n*logn)。

算法稳定性

        快速排序中，开始通常用数组的第一个数作为关键数据（基准数），然后将所有比它小的数都放到它左边，所有比它大的数都放到它右边，这个过程称为一趟快速排序。

        值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

        所以快速排序是一种不稳定排序算法。