排序算法之归并排序

简介

        归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

        将已有序的子序列合并；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

基本思想

        归并排序采用经典的分治策略，而分治法就是将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之。

        简单来讲，归并排序将序列递归拆分成两两的子序列，直到子序列长度为1，递归深度为 \(\log_2 n\)。然后将两个有序的子序列合并成一个有序序列，一直向上合并，最终完成排序。

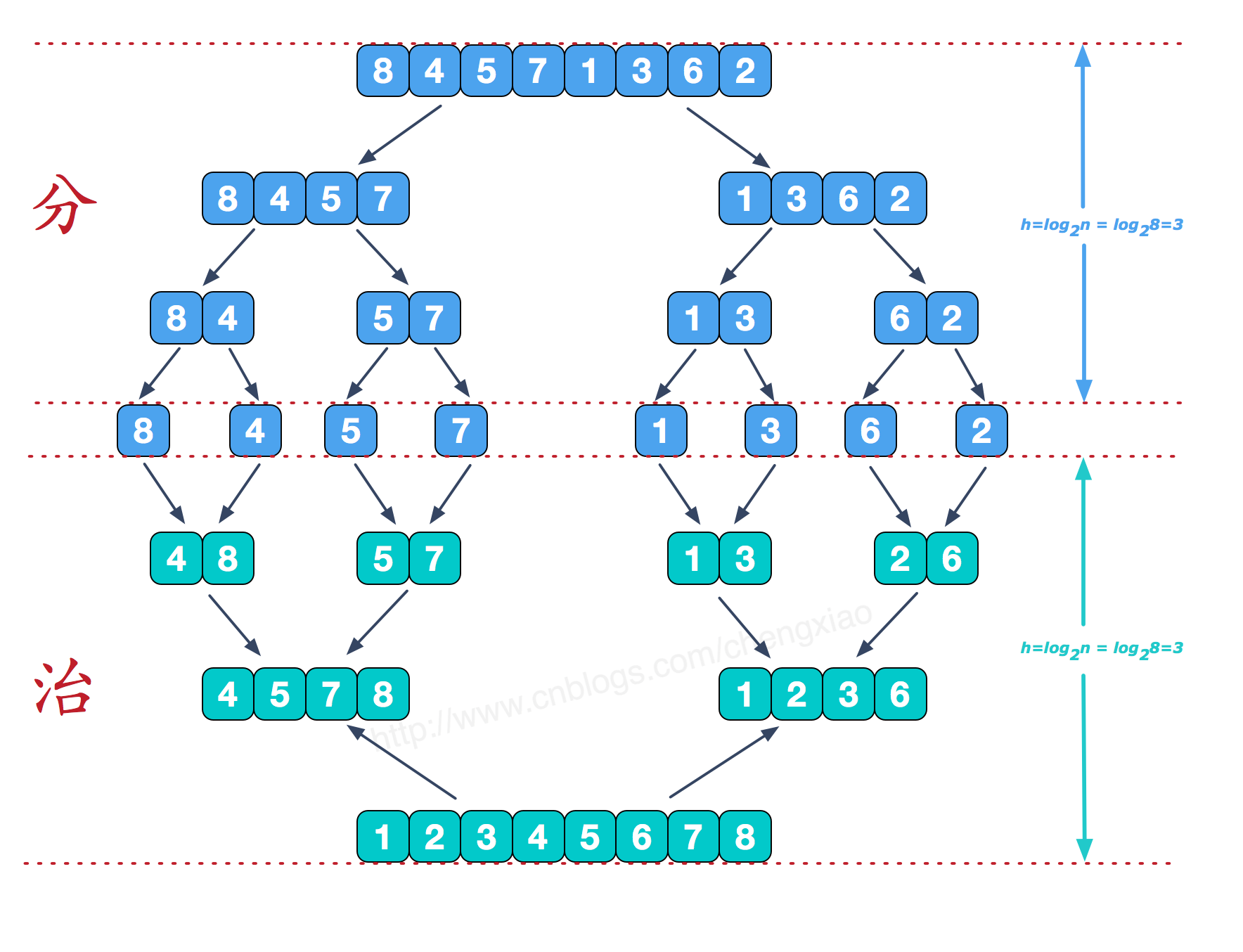
（图片参考：https://www.cnblogs.com/chengxiao/p/6194356.html）

排序过程

        此处排序数据：{3,44,37,5,47,15,4,19,50,48}

代码实现

/**
 * 归并排序
 * @Author distance
 */
public class MergeSort {

    public static void merge(int[] num, int left, int mid, int right, int[] temp) {
        //一个新的数组，将原数组映射进去
        for (int i = left; i <= right; i++) {
            temp[i] = num[i];
        }

        // 序列1 left ~ mid	  序列2 mid+1 ~ right
        // 有序合并
        int headL = left, headR = mid + 1; // headL 和 headR 分别指向两个序列开头部分
        int head = left; // 原序列起点

        while (headL <= mid && headR <= right) {
            if (temp[headL] < temp[headR]) {
                num[head ++] = temp[headL];
                headL ++;
            } else {
                num[head ++] = temp[headR];
                headR ++;
            }
        }

        while (headL <= mid) {
            num[head ++] = temp[headL];
            headL ++;
        }

        while (headR <= right) {
            num[head ++] = temp[headR];
            headR ++;
        }
    }

    public static void mergeSort(int[] num, int left, int right, int[] temp) {
        if (left >= right) {
            return;
        }

        int mid = (left + right) / 2;
        mergeSort(num, left, mid, temp);
        mergeSort(num, mid + 1, right, temp);

        merge(num, left, mid, right, temp);
    }

    public static void sort(int[] num) {

        int[] temp = new int[num.length];
        mergeSort(num, 0, num.length - 1, temp);
    }

    public static void main(String[] args) {
        int[] num = {3,44,37,5,47,15,4,19,50,48};
        MergeSort.sort(num);

        for (int i = 0; i < num.length; i++) {
            System.out.print(num[i] + " ");
        }
    }
}

算法分析

时间复杂度

        归并排序的最好、最坏和平均时间复杂度都是 \(O(n * logn)\)，而空间复杂度是 \(O(n)\)。

        算法比较次数介于 \((n * logn) / 2\) 和 \((n * logn) - n+1\) 之间，赋值操作的次数是 \((2n * logn)\)。

        因此可以看出，归并排序算法比较占用内存，但却是效率高且稳定的排序算法。

        所以归并排序的平均时间复杂度为 O(n*logn)。

算法稳定性

        归并排序是稳定的排序，即相等的元素的顺序不会改变。

        例如输入序列 1(1) 3(2) 2(3) 2(4) 5(5) 时输出的 1(1) 2(3) 2(4) 3(2) 5(5) 中的 2 和 2 是按输入的顺序，这对要排序数据包含多个信息而要按其中的某一个信息排序，要求其它信息尽量按输入的顺序排列时很重要。

        归并排序的比较次数小于快速排序的比较次数，移动次数一般多于快速排序的移动次数。

        所以归并排序是一种稳定排序算法。