排序算法之冒泡排序

简介

        冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。

        它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

        这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。

基本思想

        （1）比较相邻的元素。如果第一个比第二个大，就交换他们两个。

        （2）对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

        （3）针对所有的元素重复以上的步骤，除了最后一个。

        （4）持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

排序过程

        此处排序数据：{29,10,14,37,13,14}

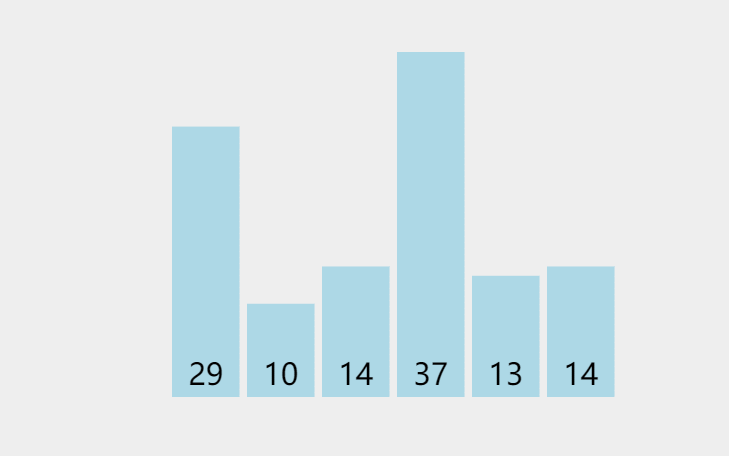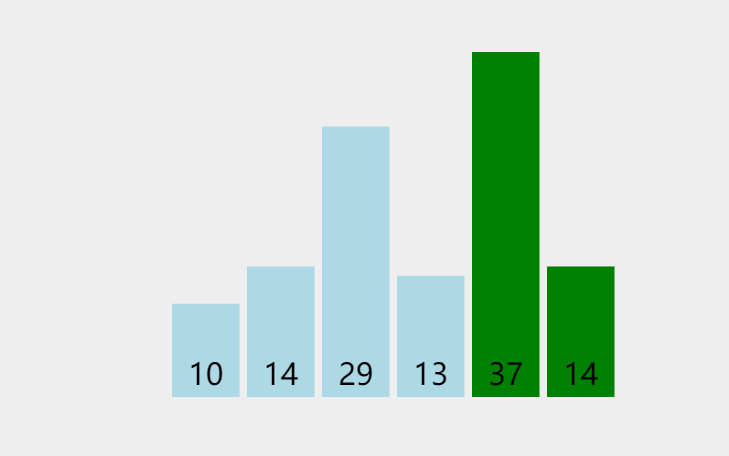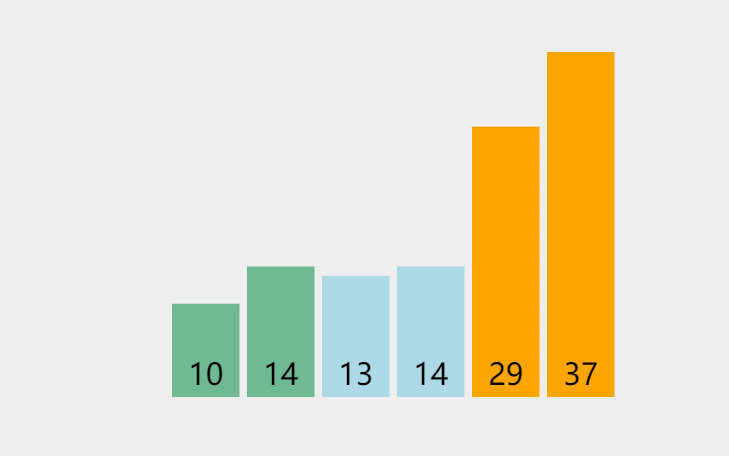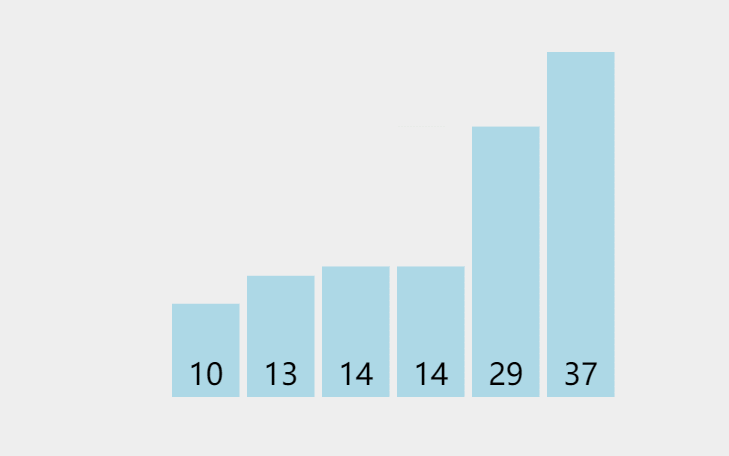
代码实现

/**
 * 冒泡排序
 * @Author distance
 */
public class BubbleSort {

    public static void sort(int[] num) {
        int temp;
        for (int i = 0; i < num.length - 1; i++) {
            for (int j = 0; j < num.length - i -1; j++) {
                if (num[j] > num[j+1]) {
                    temp = num[j];
                    num[j] = num[j+1];
                    num[j+1] = temp;
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] num = {29,10,14,37,13,14};

        BubbleSort.sort(num);

        for (int i = 0; i < num.length; i++) {
            System.out.print(num[i] + " ");
        }
    }
}

代码优化

        有没有更优化的实现方式呢？

        我们先来分析一下，结合代码我们发现冒泡排序有两次for循环，这不是一个高效的算法。如果说我们能够减少冒泡的次数，则可以极大的提升算法的执行效率。

        其实我们只要结合冒泡排序算法的核心思想后半部分：比较交换相邻的元素。如果在一轮冒泡中，没有发生相邻元素的交换，那说明序列已经有序了，不管后面还剩下多少次冒泡，我们都不需要再进行冒泡下去了。这样就减少了冒泡的次数。

        关于减少冒泡次数的分析，如果你暂时没有理解，没有关系。请看下面的代码实现。

/**
 * 冒泡排序优化
 * @Author distance
 */
public class BubbleSort {

    public static void sort(int[] num) {
        int temp;
        for (int i = 0; i < num.length - 1; i++) {
            boolean flag = false;	// 设置标志位
            for (int j = 0; j < num.length - i - 1; j++) {
                if (num[j] > num[j+1]) {
                    temp = num[j];
                    num[j] = num[j+1];
                    num[j+1] = temp;
                    flag = true;	// 交换了
                }
            }
            if (!flag) {	// 未交换，已经有序了，停止排序
                break;
            }
        }
    }

    public static void main(String[] args) {
        int[] num = {29,10,14,37,13,14};

        BubbleSort.sort(num);

        for (int i = 0; i < num.length; i++) {
            System.out.print(num[i] + " ");
        }
    }
}

算法分析

时间复杂度

        如果初始状态已经是正序的，一趟扫描即可完成排序。所需的关键字比较次数为 n-1​ 次和移动次数为 0，均达到最小值。所以，冒泡排序最好的时间复杂度为 O(n)。

        如果初始状态是反序的，需要进行 n-1 趟排序。每趟排序要进行 n-i 次关键字的比较 (1≤i≤n-1)，且每次比较都必须移动数字三次来达到交换位置。在这种情况下，比较和移动次数均达到最大值。

        冒泡排序的最坏时间复杂度为 O(n^2)。

        综上，因此冒泡排序总的平均时间复杂度为 O(n^2)。

算法稳定性

        冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。

        所以，如果两个元素相等，是不会再交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变。

        所以冒泡排序是一种稳定排序算法。