20202312郭威 实验九 《面向对象程序设计》实验报告
2002312 2021-2022-1 实验九 《图》实验报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 郭威
学号:20202312
实验教师:王志强
实验日期:2021年12月9日
必修/选修: 必修
1.实验内容
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
PS:本题12分。目前没有明确指明图的顶点和连通边,如果雷同或抄袭,本次实验0分。
实验报告中要根据所编写的代码解释图的相关算法
2.实验过程及结果
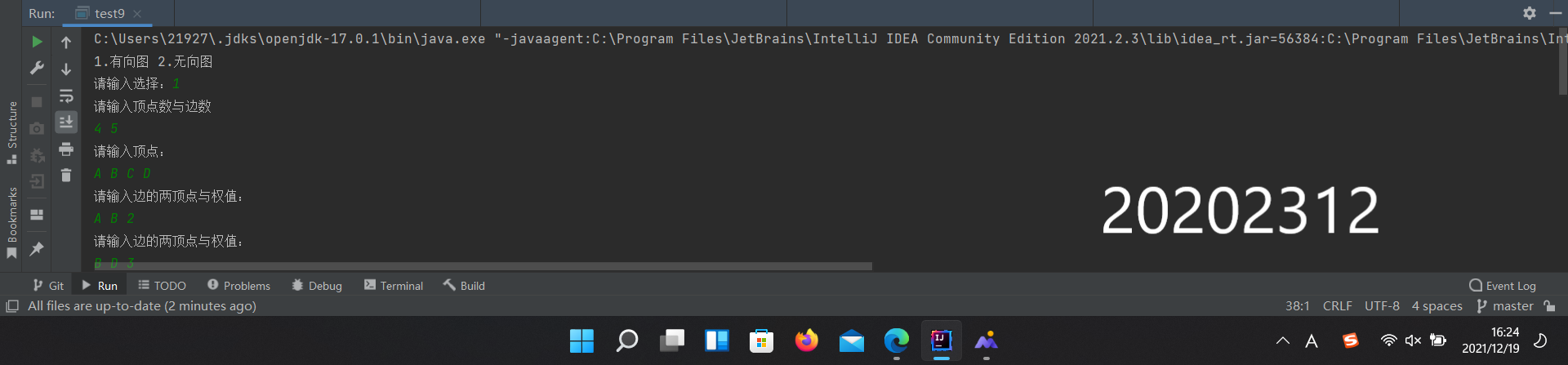
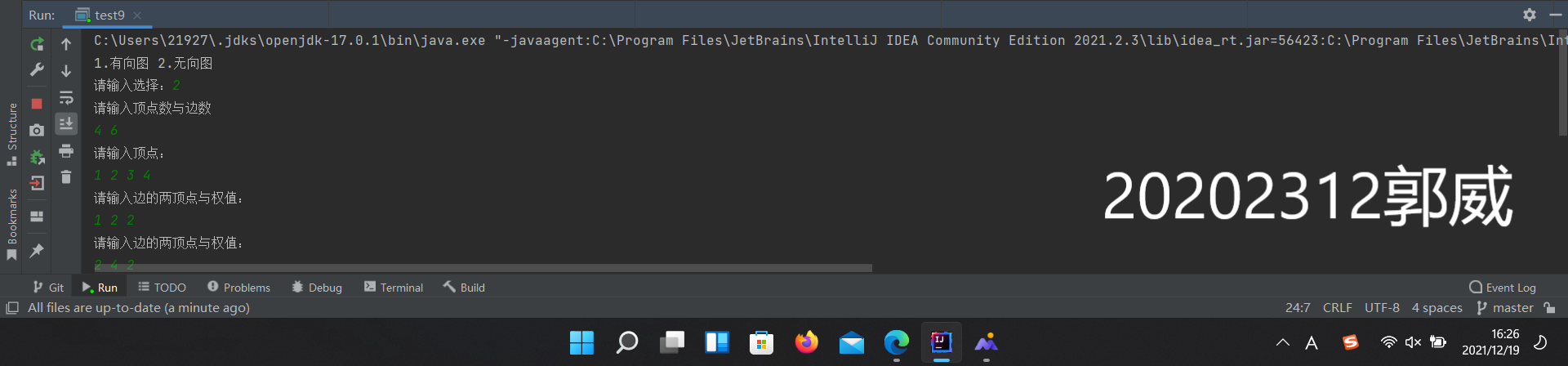
(1)初始化
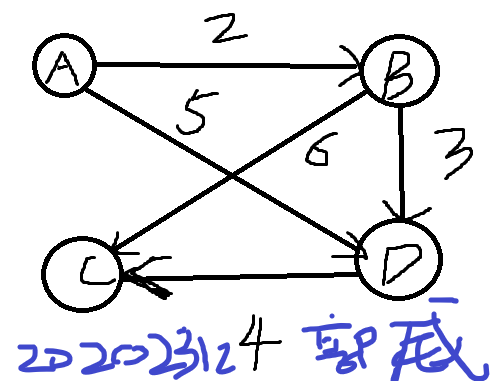
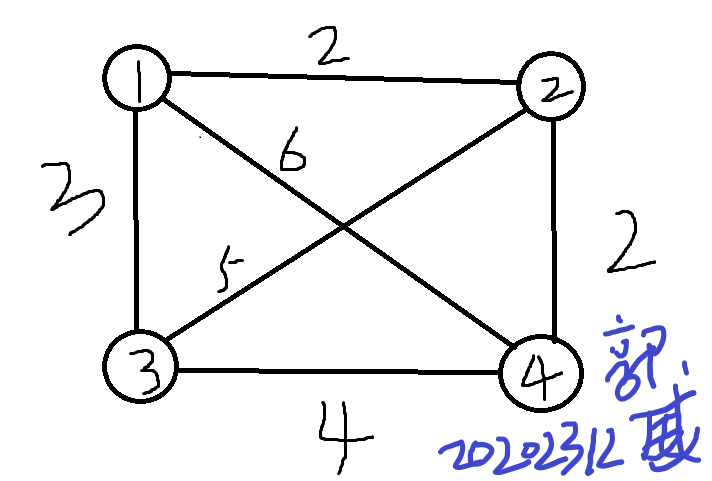

1 public class Graph {
2 Vertex[] VertexArray;
3 Edge[] EdgeArray;
4 int edgenum,vertexnum;
5 int adjmatrix[][];
6 public void CreateGraph(int num)
7 {
8 Scanner scan = new Scanner(System.in);
9 System.out.println("请输入顶点数与边数");
10 vertexnum=scan.nextInt();
11 edgenum=scan.nextInt();
12 adjmatrix=new int[vertexnum][vertexnum];
13 VertexArray=new Vertex[vertexnum];
14 EdgeArray=new Edge[edgenum];
15 System.out.println("请输入顶点:");
16 for(int i=0;i<vertexnum;i++){
17 VertexArray[i]=new Vertex(scan.next());
18 }
19 for(int i=0;i<edgenum;i++){
20 String a,b;
21 Vertex from,to;
22 int c;
23 System.out.println("请输入边的两顶点与权值:");
24 from=SearchVertex(scan.next());
25 to=SearchVertex(scan.next());
26 c= scan.nextInt();
27 EdgeArray[i]=new Edge(from,to,c);
28 adjmatrix[SearchIndex(from.name)][SearchIndex(to.name)]=c;
29 from.outdegree++;
30 to.indegree++;
31 if(num==2){
32 adjmatrix[SearchIndex(to.name)][SearchIndex(from.name)]=c;
33 from.outdegree--;
34 to.indegree--;
35 }
36 }
37 }
38
39 public int SearchIndex(String name){
40 for(int i=0;i<VertexArray.length;i++)
41 {
42 if(VertexArray[i].name.equals(name))
43 return i;
44 }
45 return -1;
46 }
47
48 public Vertex SearchVertex(String name)
49 {
50 for(int i=0;i<VertexArray.length;i++){
51 if(VertexArray[i].name.equals(name))
52 return VertexArray[i];
53 }
54 return null;
55 }
(2) 图的遍历:
1 public String BreadthFirstTraversal(String first){
2 Vertex temp;
3 String result="";
4 Queue<Vertex> queue=new LinkedList();
5 queue.offer(SearchVertex(first));
6 SearchVertex(first).Mark();
7 while(!queue.isEmpty()){
8 temp=queue.poll();
9 result+=temp.name;
10 for(int i=0;i<vertexnum;i++){
11 if(adjmatrix[SearchIndex(temp.name)][i]!=0&&!VertexArray[i].isMark) {
12 queue.offer(VertexArray[i]);
13 VertexArray[i].Mark();
14 }
15 }
16 }
17 for(int i=0;i<vertexnum;i++){ VertexArray[i].wipe(); }
18 return result;
19 }
20 public String DepthTraversal(String first){
21 String result=first;
22 SearchVertex(first).Mark();
23 for(int i=0;i<vertexnum;i++){
24 if(adjmatrix[SearchIndex(first)][i]!=0&&!VertexArray[i].isMark) {
25 result += DepthTraversal(VertexArray[i].name);
26 }
27 }
28 return result;
29 }
30 public String DepthFirstTraversal(String first){
31 String a=DepthTraversal(first);
32 for(int i=0;i<vertexnum;i++){ VertexArray[i].wipe(); }
33 return a;
34 }
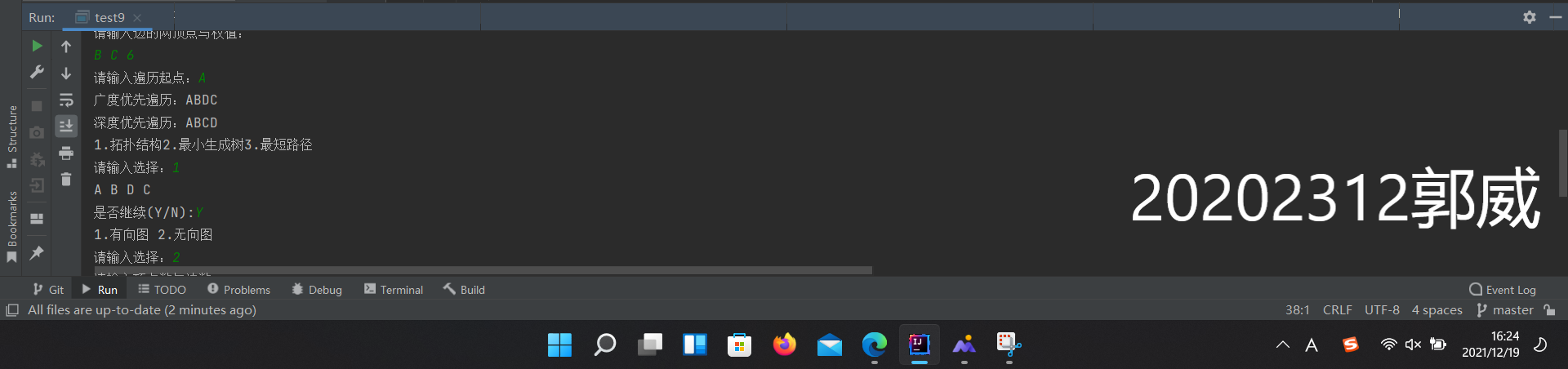

(3) 有向图的拓扑排序
1 public String topology(){
2 String a="";
3 Stack<Vertex> stack=new Stack<Vertex>();
4 int indegreearray[]=new int[vertexnum];
5 boolean ismark[]=new boolean[vertexnum];
6 for(int i=0;i< VertexArray.length;i++) {
7 indegreearray[i] = VertexArray[i].indegree;
8 ismark[i]=false;
9 if(indegreearray[i]==0){stack.push(VertexArray[i]);ismark[i]=true;}
10 }
11 while(!stack.isEmpty()) {
12 Vertex temp = stack.pop();
13 a += temp.name + " ";
14 for (int i = 0; i < vertexnum; i++) {
15 if (adjmatrix[SearchIndex(temp.name)][i]!=0) {
16 indegreearray[i]--;
17 for (int j = 0; j < vertexnum; j++) {
18 if (indegreearray[j] == 0 && !ismark[j]) { stack.push(VertexArray[j]);ismark[j] = true; }
19 }
20 }
21 }
22 }
23 for(int i=0;i<vertexnum;i++)
24 if(!ismark[i])return "该图存在环";
25 return a;
26 }
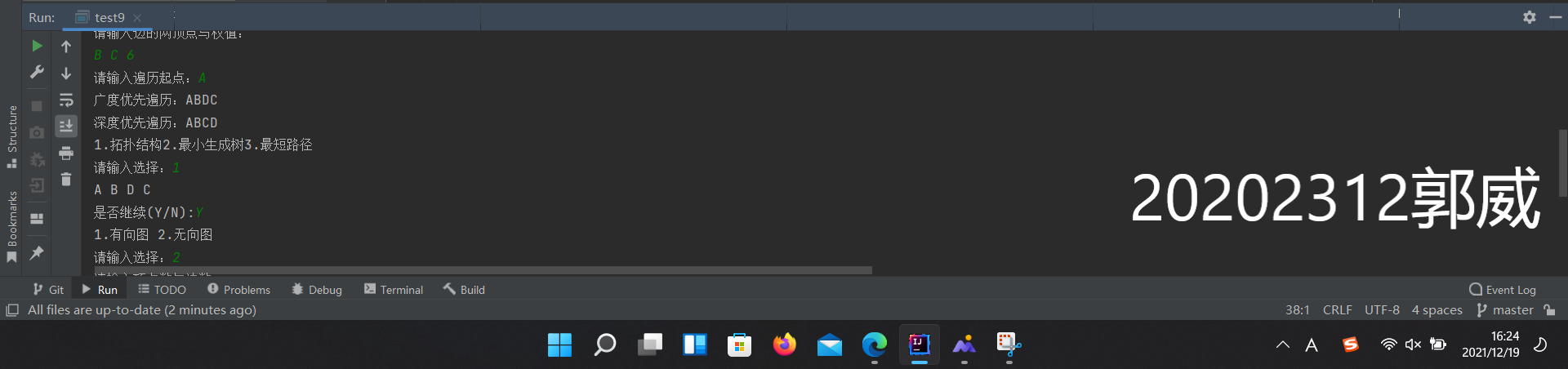
(4) 完成无向图的最小生成树
1 public Graph spanningTree(){
2 Graph spanning =new Graph();
3 Scanner scan=new Scanner(System.in);
4 Edge []an=new Edge[vertexnum-1];
5 int anweight[]=new int[vertexnum-1];
6 String a="";
7 spanning.VertexArray=this.VertexArray;
8 spanning.EdgeArray=new Edge[vertexnum-1];
9 spanning.edgenum=vertexnum-1;
10 spanning.vertexnum=vertexnum;
11 System.out.print("请输入起点:");
12 Vertex as= SearchVertex(scan.next());
13 boolean appear=false;
14 for(int i=0;i<vertexnum-1;i++){
15 an[i]=new Edge();
16 an[i].from=as;
17 if(VertexArray[i]==as)appear=true;
18 if(appear)an[i].to=VertexArray[i+1];
19 else an[i].to=VertexArray[i];
20 for(int j=0;j<edgenum;j++){
21 if(EdgeArray[j].from==an[i].from&&EdgeArray[j].to==an[i].to) {an[i].weight=EdgeArray[j].weight;break;}
22 if(EdgeArray[j].from==an[i].to&&EdgeArray[j].to==an[i].from){an[i].weight=EdgeArray[j].weight;break;}
23 }
24 }
25 for(int r=0,min=0,max=0;r<vertexnum-1;r++){
26 for(int j=0;j<vertexnum-1;j++){
27 if(an[j].weight<an[min].weight&&an[j].weight>0&&anweight[j]>=0){min=j;}
28 if(an[j].weight>an[max].weight&&an[j].weight>0&&anweight[j]>=0){max=j;}
29 }
30 anweight[min]=-1;
31 spanning.EdgeArray[r]=an[min];
32 a+=an[min].from.name+" "+an[min].to.name+" "+an[min].weight+"\n";
33 for(int t=0;t<vertexnum-1;t++){
34 for(int j=0;j<edgenum;j++){
35 if(EdgeArray[j].from==an[min].to&&EdgeArray[j].to==an[t].to&&anweight[t]>=0) {
36 anweight[t]=EdgeArray[j].weight;
37 break;}
38 if(EdgeArray[j].from==an[t].to&&EdgeArray[j].to==an[min].to&&anweight[t]>=0){
39 anweight[t]=EdgeArray[j].weight;
40 break;}
41 }
42 if(anweight[t]<an[t].weight&&anweight[t]>0){an[t].from=an[min].to;an[t].weight=anweight[t];}
43 if(an[t].weight==-1){an[t].from=an[min].to;an[t].weight=anweight[t];}
44 }
45 min=max;
46 }
47 System.out.println(a);
48 return spanning;
49 }
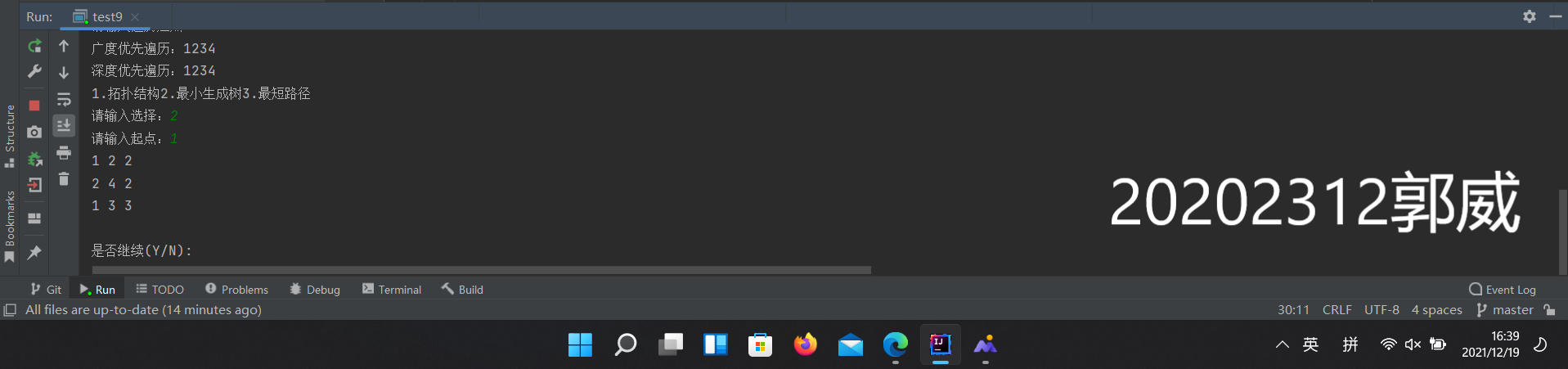
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)
1 public void Dijkstra(){
2 Scanner scan=new Scanner(System.in);
3 String a="",b="";
4 System.out.print("请输入起点");
5 b=scan.next();
6 Vertex begin=SearchVertex(b);
7 Path ShortestEdge[]=new Path[vertexnum];
8 Path shortest[]=new Path[vertexnum-1];
9 for(int i=0,j=0;i<vertexnum;i++){
10 if(VertexArray[i]!=begin) {
11 ShortestEdge[j]=new Path(begin,VertexArray[i],1000000000);j++;
12 }
13 }
14 for(int i = 0,k=0; i<vertexnum-1;i++){
15 Path min=new Path();
16 Path con=new Path(3);
17 for(int j=0;j<vertexnum;j++){
18 int tempweight=adjmatrix[SearchIndex(begin.name)][j];
19 if(SearchIndex(begin.name)!=j) {
20 if (ShortestEdge[k].weight!= con.weight) {
21 Path temp1 =new Path(ShortestEdge[k]), temp2 ;
22 if(i>0) temp2 =new Path(shortest[i-1]);
23 else temp2=ShortestEdge[k];
24 if (tempweight != 0 &&temp2.Add(begin, ShortestEdge[k].end, tempweight).weight < temp1.weight){
25 ShortestEdge[k]=temp2;
26 }
27 else {
28 ShortestEdge[k] = temp1;
29 }
30 if (ShortestEdge[k].weight < min.weight) min = ShortestEdge[k];
31 }
32 k++;
33 }
34 }
35 ShortestEdge[vertexnum-1]=new Path(min);
36 shortest[i]=new Path(min);
37 a+=b+" "+shortest[i].end.name+" "+shortest[i].weight+"\n";
38 begin=min.end;
39 min.weight=con.weight;
40 k=0;
41 }
42 System.out.println(a);
43 }

3.实验过程中遇到的问题和解决过程
- 问题1:在输入无向图时老是报错,进行调试也没能解决
- 问题1解决方案:仔细查找,发现是自己的输入方式出现了问题,调整后,显示成功。
## 其他(感悟、思考等)
感觉这次图的实验好难啊,好多算法自己还不是很清楚,感觉还得多花时间去搞懂。
## 参考资料
- [《Java程序设计与数据结构教程(第二版)》](https://book.douban.com/subject/26851579/)
- [《Java程序设计与数据结构教程(第二版)》学习指导](http://www.cnblogs.com/rocedu/p/5182332.html)
- ...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号