排序——归并排序和快速排序
1,归并排序的基本思想:
1,将两个或两个以上的有序序列合并成一个新的有序序列,比如有序序列
v[0] ... v[m] 和 v[m+1] ... v[n-1] 合并为 v[0] ... v[n-1],这种归并方法称为 2 路归并;
1,必须大于 1 个有序序列;
2,必须有序;
2,归并的套路:
1,将 3 个有序序列归并为一个新的有序序列,称为 3 路归并;
2,将 N 个有序序列归并为一个新的有序序列,称为 N 路归并;
3,将多个有序序列归并为一个新的有序序列,称为多路归并;
3,2 路归并示例:

4,归并排序的代码实现及其示例:
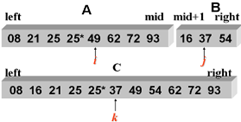
1,归并要用额外的空间;
5,归并排序 Sort::Merge 的实现:
1 /* 实现 Merge 函数,真正的做归并的操作了 */ 2 template <typename T> 3 static void Merge(T src[], T helper[], int begin, int mid, int end, bool min2max) 4 { 5 int i = begin; // 代表左边的起始位置 6 int j= mid + 1; // 代表右边的起始位置 7 int k = begin; // 代表辅助空间的起始位置 8 9 /* 对两路 for 循环的把控,这个 while 循环很经典 */ 10 while( (i <= mid) && (j <= end) ) // 左边 i 和 右边 j 都还没有达到尾部 11 { 12 if( min2max ? (src[i] < src[j]) : (src[i] > src[j]) ) // min2max 真,将小的赋值到辅助空间,很经典 13 { 14 helper[k++] = src[i++]; // 先将左边的元素放入辅助空间中,并继续在 while 中比较 15 } 16 else 17 { 18 helper[k++] = src[j++]; // 右边的较小,放入辅助空间中 19 } 20 } 21 22 while( i <= mid ) // 当上面的某一路达到尾部没有了,而另一路还有元素的时候,当这一路是左边的元素时 23 { 24 helper[k++] = src[i++];// 直接将左边剩余空间中的元素拷贝到辅助空间中 25 } 26 27 while( j <= end ) // 当上面的某一路达到尾部没有了,而另一路还有元素的时候,当这一路是右边的元素时 28 { 29 helper[k++] = src[j++];// 直接将右边剩余空间中的元素拷贝到辅助空间中 30 } 31 32 for(i=begin; i<=end; i++) // 将最终的元素全都从辅助空间拷贝到原始的空间中去 33 { 34 src[i] = helper[i]; 35 } 36 } 37 38 /* 二路归并排序,需要递归排序完成;第一个参数是需要归并排序的数据,第二个参数是归并排序的辅助空间,第三个参数是排序范围中的起始位置,第四个参数是排序范围中的结束位置;*/ 39 template <typename T> // 递归 40 static void Merge(T src[], T helper[], int begin, int end, bool min2max) 41 { 42 if( begin < end ) // 递归的出口,只有一个元素的时候,就是有序的,此时 begin == end;递归函数的参数自动的变化 43 { 44 int mid = (begin + end) / 2; // 将需要排序的序列平均的分成两路,mid 之前是一路、之后是一路 45 Merge(src, helper, begin, mid, min2max); // 对左边的这一路进行排序 46 Merge(src, helper, mid+1, end, min2max); // 对右边的这一路进行排序 47 Merge(src, helper, begin, mid, end, min2max); // 对两路进行归并合并,从 begin 到 mid, 从 mid 到 end,并拷贝到原始数组 48 } 49 } 50 51 /* 归并排序,这个函数对接口的处理很到位 */ 52 template <typename T> // 需要额外的空间才能完成,空间复杂度为 O(n),时间复杂度为 O(n*logn),稳定的排序法 53 static void Merge(T array[], int len, bool min2max = true) 54 { 55 T* helper = new T[len]; // 从堆空间申请待排序长度的辅助空间 56 57 /* 申请成功,进行具体的归并排序 */ 58 if( helper != NULL ) 59 { 60 Merge(array, helper, 0, len-1, min2max); 61 } 62 63 delete[] helper; 64 }
6,快速排序的基本思想:
1,任取序列中的某个数据元素作为基准将整个序列划分为左右两个子序列:
1,左侧子序列中所有元素都小于或等于基准元素;
2,右侧子序列中所有元素都大于基准元素;
3,基准元素排在这两个子序列中间;
2,分别对这两个子序列重复进行划分,直到所有的数据元素都排在相应位置上为止;
7,快速排序示例和元素排序示例及示例分析:


1,划分的结果就是基准就位,返回值就是基准就位的下标;
8, 快速排序 Sort::Quick 实现(仅 *.cpp 文件):
1 /* 快速排序的分割函数,返回值是下标,所以是 int,对数组 array[] 进行划分,二三两个参数为划分范围 */ 2 template <typename T> 3 static int Partition(T array[], int begin, int end, bool min2max) 4 { 5 T pv = array[begin]; // 把第一个位置处的数据元素作为分割的基准 6 7 while( begin < end ) // 当begin和end相等的时候结束;这里一定会相等的 8 { 9 while( (begin < end) && (min2max ? (array[end] > pv) :(array[end] < pv)) ) // 实现不同顺序的排序 10 { 11 end--; // 当从最右边开始的数大于基准的时候,不交换位置,再换下一个位置比较 12 } 13 14 Swap(array[begin], array[end]); // 把较小的数据元素放到前面,然后开始下面的较小端的比较,能够直接使 begin 先加 1,交换元素 15 16 while( (begin < end) && (min2max ? (array[begin] <= pv) : (array[begin] >= pv)) ) // 实现不同顺序的排序 17 { 18 begin++; // 当从最左边开始的数据元素小宇基准,不交换位置,再换下一个位置比较 19 } 20 21 Swap(array[begin], array[end]); // 把较大的数据元素放到后面,然后开始下面的较大端的比较,能够直接使 end 再加 1 22 } 23 24 array[begin] = pv; // 将分割的基准值放到合适的位置 25 return begin; // 返回基准最终下标 26 } 27 28 /* 递归实现快速排序 */ 29 template <typename T> 30 static void Quick(T array[], int begin, int end, bool min2max ) 31 { 32 if( begin < end ) // 起始位置小于终止位置,则待排序的序列他不是一个元素,进行递归;这里是为什么,是因为这里的递归递归到最后了,传进来的 begin 和 end 参数此时相等,已经不需要排序了 33 { 34 int pivot = Partition(array, begin, end, min2max); // 基准最终所处//的位置 35 Quick(array, begin, pivot-1, min2max); // 左边的位置进行快速排序; 36 Quick(array, pivot+1, end, min2max); // 右边的位置进行快速排序; 37 } 38 } 39 40 /* 快速排序 */ 41 template <typename T> // 时间复杂度是 O(n*logn),不稳定排序 42 static void Quick(T array[], int len, bool min2max = true) 43 { 44 Quick(array, 0, len-1, min2max); 45 } 46 template <typename T> // 时间复杂度是 O(n*logn),不稳定排序 47 static void Quick(T array[], int len, bool min2max = true) 48 { 49 Quick(array, 0, len-1, min2max); 50 }
9,小结:
1,归并排序需要额外的辅助空间才能完成,空间复杂度为 O(n);
2,归并排序的时间复杂度为 O(n*logn),是一种稳定的排序法;
3,快速排序通过递归的方式对排序问题进行划分;
4,快速排序的时间复杂度为 O(n*logn),是一种不稳定的排序法;


